Forward search in multivariate analysis with automatic outlier detection procedure
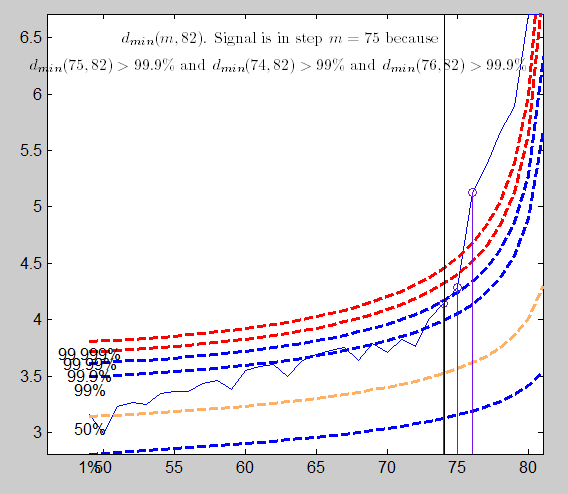
The forward search in multivariate analysis used for outlier detection purposes examines the minimum Mahalanobis distance (MD) among observations that are not in the subset (say of size m). If this ordered observation is an outlier relative to the other m observations, this distance will be ‘large" compared with the maximum MD of observations in the subset. In uncalibrated use of the minimum MD to detect outliers the decision whether a difference in distances is ‘large" is subjective, without reference to any null distribution. To calibrate the forward search and so to provide an objective basis for decisions about the number of outliers in a sample we consider the distribution of the minimum MD in the forward search. The output is a series of theoretical simultaneous confidence bands (envelopes) associated to the quantiles of the distribution of the minimum MD.
To use the envelopes in the forward search for outlier detection we follow a two-stage process. In the first stage we run a search on the data, monitoring the bounds for all n observations until we obtain a "signal" indicating that observation m^\dagger and therefore succeeding observations, may be outliers, because the value of the statistic lies beyond our threshold. In the context of signal detection, we have tried to take into account the fact that the envelopes of minimum deletion residual outside subset consist roughly of three parts; an initial decreasing part, a "central" roughly flat part and a steeply curving "final" part. Once a signal has been found (e.g. three consecutive values of minimum MD above a certain threshold), we superimpose envelopes for values of n from this point until the first time that we introduce an observation we recognize as an outlier.
Example 1
The code below loads the heads dataset and launch the automatic outlier detection procedure
% Load the data
load('head');
Y=head{:,:};
% Use function FSM (Forward search in multivariate analysis with automatic outlier detection purposes)
[out]=FSM(Y);
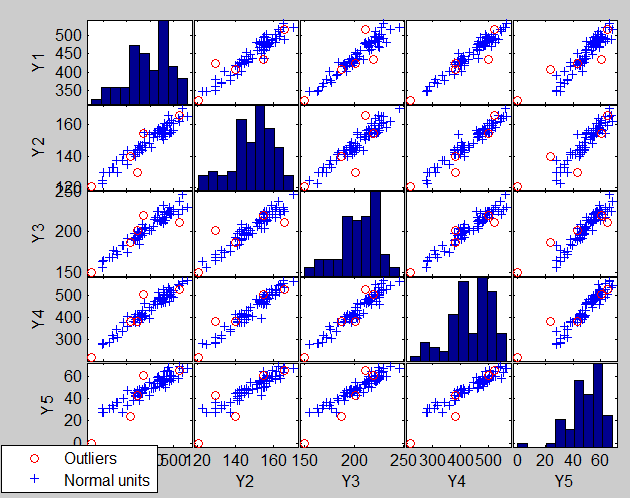
The plot of the Minimum Mahalanobis distance among observations outside the subset and the scatterplot matrix, that we report below, are produced. They show that no outlier has been detected.
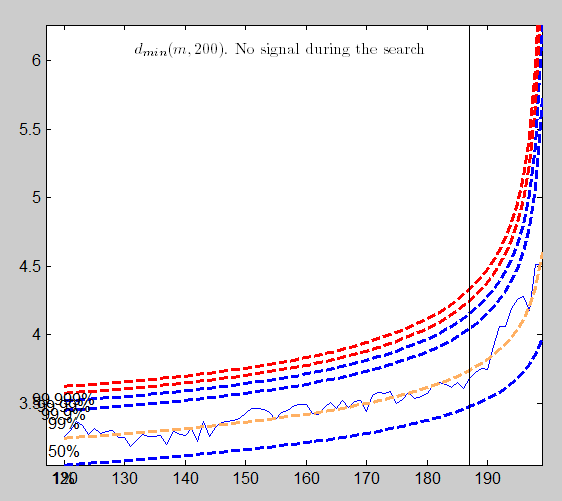
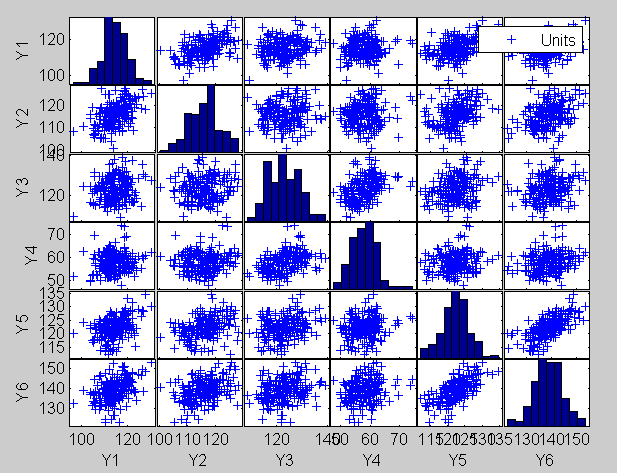
Example 2
The code below loads the mussels dataset and performs an automatic outlier detection procedure in the original scale and then in the BoxCox transformed scale.
Analysis on the original scaleload('mussels.mat');
Y=mussels{:,:};
FSM(Y);
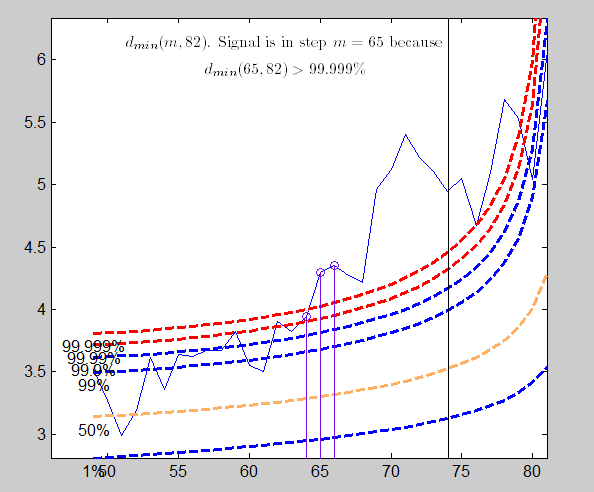
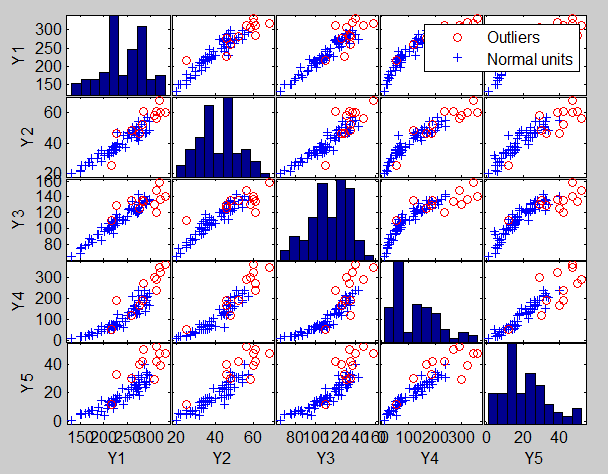
Analysis on the transformed scale
load('mussels.mat');
Y=mussels{:,:};
la=[0.5 0 0.5 0 0];
v=size(Y,2);
Y=normBoxCox(Y,1:v,la);
FSM(Y)
| Functions |
• The developers of the toolbox• The forward search group • Terms of Use• Acknowledgments