Multivariate transformations: confirmatory analysis

 

The purpose of this page is to show how it is possible to validate a certain set of transformation parameters which have been found. In this page we use the same dataset which had been used in page mult_fsmtra.html

We had found that $\lambda = (0.5, 0, 0.5, 0, 0)$ was a reasonable set of transformation parameters and that this transformation was supported by all the data except the outliers.

In this page we use the multivariate fan plot of Figure below to confirm these values of λ.

% Mussels data.
load('mussels.mat');
Y=mussels{:,:};
plotslrt=struct;
plotslrt.ylim=[-6.2 6.2];
[out]=FSMfan(Y,[0.5 0 0.5 0 0],'laAround',[-1 -0.5 0 1/3 0.5 1],'init',58,'plotslrt',plotslrt);
% Compare this plot with Figure 4.24 p. 182 of ARC (2004)

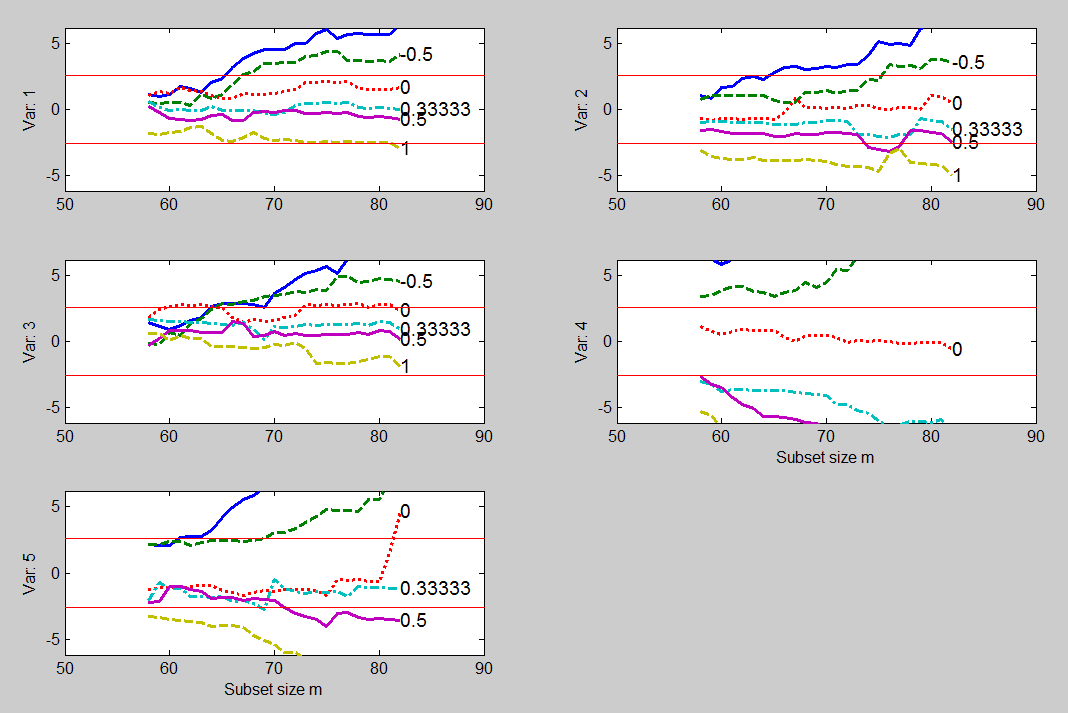
This Figure shows the evolution of the score statistics during 30 forward searches. The panels confirm the transformation we have found, but also show what other transformation is acceptable for each variable. The transformation for $y_1$ is not very tightly defined, with the statistics for 0.5 and 1/3 close to zero throughout the search and the log transformation within the 99% band. For $y_2$ the statistic for the log transformation is closest to zero throughout, although 1/3 is also acceptable. For $y_3$ the value of 1/3 is a little better than is 0.5: the other four values are unacceptable. The transformation for $y_4$ is unambiguously the log. The statistics for the other five values of the parameter increase steadily in magnitude throughout the search. Interestingly, there is no evidence of an effect of the outliers. The effect of the outliers is however evident in the last panel, that for transformation of $y_5$. The statistic for $\lambda_5=0$ is close to zero until the end of the search when the outliers enter. The one third transformation gives a statistic which is stable and close to zero at the end of the search. However it has negative values earlier on, which are significant at the 5% level.

In Atkinson Riani and Cerioli (2004) it is possible to find a detailed comparison of the data before and after the transformation.