Powertra
Powertra computes power transformation (Box-Cox or Yeo-Johnson)
Description
Examples
Transform value 1, 2, 3, 4 and 5.
y=(1:5)';
y1=Powertra(y,0.2);
plot(y,y1)
xlabel('Original values')
ylabel('Transformed values using BoxCox')
 Comparison between Box-Cox and Yeo-Johnson transformation.
Comparison between Box-Cox and Yeo-Johnson transformation.
 Comparison between Box-Cox and Yeo-Johnson transformation.
Comparison between Box-Cox and Yeo-Johnson transformation.
close all
y=(-2:0.1:2)';
n=length(y);
la=-1:1:3;
nla=length(la);
YtraYJ=zeros(n,nla);
YtraBC=nan(n,nla);
posy=y>0;
for j=1:nla
YtraYJ(:,j)=Powertra(y,la(j),'family','YJ','Jacobian',false);
YtraBC(posy,j)=Powertra(y(posy),la(j),'family','BoxCox','Jacobian',false);
end
subplot(1,2,1)
plot(y,YtraYJ)
for j=1:nla
text(y(1), YtraYJ(1,j),['\lambda=' num2str(la(j))])
end
xlabel('Original values')
ylabel('Transformed values')
title('Yeo-Johnson transformation')
subplot(1,2,2)
plot(y,YtraBC)
xlim([y(1) y(end)])
for j=1:nla
text(y(16), YtraBC(22,j),['\lambda=' num2str(la(j))])
end
xlabel('Original values')
ylabel('Transformed values')
title('Box-Cox transformation')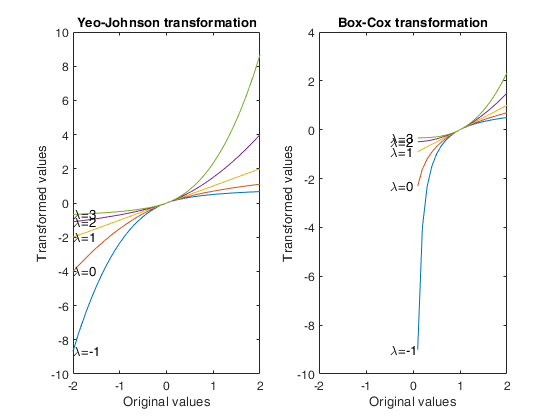
Related Examples
Mussels data.
load('mussels.mat');
Y=mussels{:,:};
la=[0.5 0 0.5 0 0];
% Transform all columns of matrix Y according to the values of la using
% the basic power transformation
Y=Powertra(Y,la,'family','basicpower');
Simulated data to check option inverse.
n=100;p=5; Y=randn(n,p); Y(3,1:3)=0; la=[0.5 0 -0.5 2 0]; family='YeoJohnson'; % Transform all columns of matrix Y according to the values of la Ytra=Powertra(Y,la,'Jacobian',false,'family',family); Ychk=Powertra(Ytra,la,'Jacobian',false,'inverse',true,'family',family); disp(max(max(abs(Y-Ychk))))
Example of the use of optional input standardize.
Mussels data.
load('mussels.mat');
Y=mussels{:,:};
la=[0.5 0 0.5 0 0];
% Transform all columns of matrix Y according to the values of la using
% the Box Cox transformation and standardize the data after
% transformation.
Y=Powertra(Y,la,'standardize',true);Input Arguments
Y — Input data.
Matrix.
n x v data matrix; n observations and v variables. Rows of Y represent observations, and columns represent variables.
Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.
Data Types: single|double
la — transformation parameters.
Vector.
k x 1 vector containing set of transformation parameters for the k ColtoTra.
Data Types: single|double
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'family','BoxCox'
, 'Jacobian',true
, 'ColtoTra',[1 2 4]
, 'inverse',true
, 'standardize',true
family
—family of transformations.string.
String which identifies the family of transformations which must be used. Possible values are 'BoxCox' (default) or 'YeoJohnson' (string YeoJohnson can be abbreviated with YJ) or 'basicpower' The Box-Cox family of power transformations equals (y^{\lambda}-1)/\ambda for \lambda not equal to zero, and log(y) if \lambda = 0.
The YJ (YeoJohnson) transformation is the Box-Cox transformation of y+1 for nonnegative values, and of |y|+1 with parameter 2-\lambda for y negative.
The basic power transformation returns y^{\lambda} if \lambda is not zero, and log(\lambda) otherwise.
Remark: BoxCox and the basic power family can be used just if input y is positive. YeoJohnson family of transformations does not have this limitation.
Example: 'family','BoxCox'
Data Types: string
Jacobian
—Requested Jacobian of transformed values.true (default) | false.
If true (default) the transformation is normalized to have Jacobian equal to 1. This option does not apply if inverse =1.
Example: 'Jacobian',true
Data Types: string
ColtoTra
—Variable to transform.vector.
k x 1 integer vector specifying the variables which must be transformed. If it is missing and length(la)=v all variables are transformed
Example: 'ColtoTra',[1 2 4]
Data Types: single|double
inverse
—Inverse transformation.logical.
If inverse is true, the inverse transformation is returned. The default value of inverse is false.
Example: 'inverse',true
Data Types: Logical
standardize
—standardize the data after transformation.logical.
If standardize is true (default is false) zero-mean, unit-variance normalization to the transformed output is applied.
Example: 'standardize',true
Data Types: Logical
Output Arguments
References
Yeo, I.K and Johnson, R. (2000), A new family of power transformations to improve normality or symmetry, "Biometrika", Vol. 87, pp. 954-959.