RKrho
RKrho computes rho function for Rocke (translated Tukey's) biweight
Syntax
rhoRK=RKrho(u,c, M)example
Examples
Related Examples
Input Arguments
Output Arguments
More About
References
Maronna, R.A., Martin D. and Yohai V.J. (2006), "Robust Statistics, Theory and Methods", Wiley, New York.
Rocke D.M. (1996), Robustness properties of S-estimators of multivariate location and shape in high dimension, "The Annals of Statistics", Vol. 24, pp. 1327-1345.

|
RKpsix |
RKwei |
 |
|
|
Functions |
|
• The developers of the toolbox • The forward search group • Terms of Use • Acknowledgments
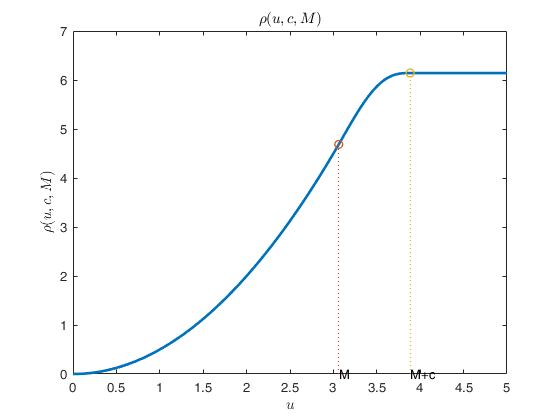
 Plot of rho function.
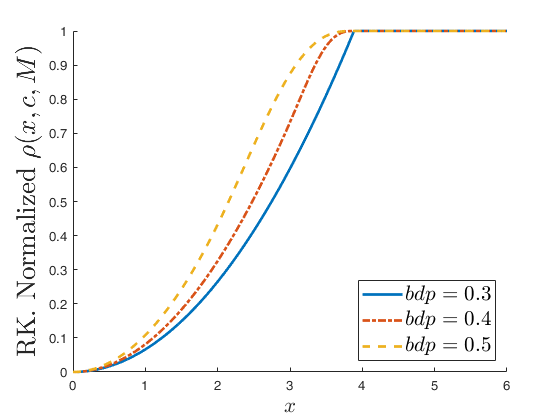
Plot of rho function.