medcouple
MEDCOUPLE computes the medcouple, a robust skewness estimator.
Syntax
Description
Examples
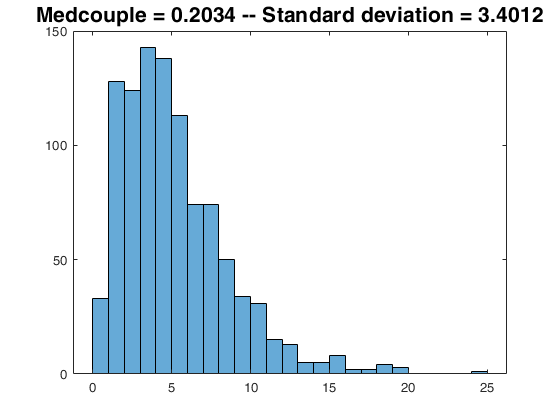
 The medcouple on small datasets.
The medcouple on small datasets.
 The medcouple on small datasets.
The medcouple on small datasets.For small n, it is better to compute the the medcouple also on the reflected sample -z and return (medcouple(z) - medcouple(-z))/2; To work on positive values we do this with:
z = chi2rnd(5,25,1);
mcm = 1; % use naive method (n is small ...)
medoutR = 0.5*(-medcouple(repmat(max(z),size(z,1),1)-z , mcm) + medcouple(z,mcm));
medout = medcouple(z,mcm);
disp('Application to a non problematic dataset:');
disp(['result with reflected option = ' num2str(medoutR) ' --- result on z only = ' num2str(medoutR)]);
Application to a non problematic dataset: result with reflected option = -0.1548 --- result on z only = -0.1548
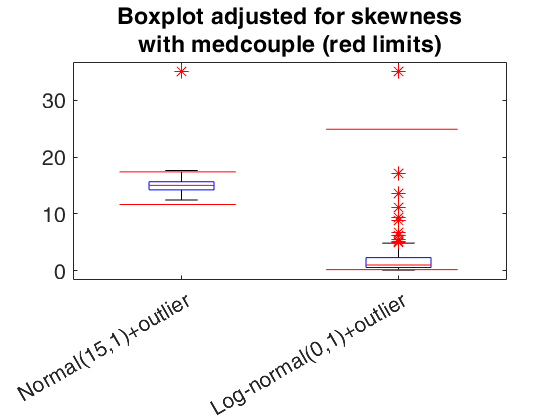
 Boxplot using medcouple to adjust for skewness.
Boxplot using medcouple to adjust for skewness.
 Boxplot using medcouple to adjust for skewness.
Boxplot using medcouple to adjust for skewness.Apply to symmetric and skewed data
rng(5);
%orientation = 'horizontal';
orientation = 'vertical';
% normal data with an outlier
datain1 = 15+randn(200,1);
datain1 = [datain1 ; 35];
% log-normal data with an outlier
datain2 = lognrnd(0,1,200,1);
datain2 = [datain2 ; 35];
k = 1.5;
% limits on normal data + one outlier
MC_1 = medcouple(datain1);
Q1_1 = quantile(datain1,0.25);
Q3_1 = quantile(datain1,0.75);
IQR_1 = Q3_1 - Q1_1;
DataLimLower_1 = Q1_1 - k * exp(-3.5 * MC_1) * IQR_1;
DataLimUpper_1 = Q3_1 + k * exp(4 * MC_1) * IQR_1;
% limits on log-normal data + one outlier
MC_2 = medcouple(datain2);
Q1_2 = quantile(datain2,0.25);
Q3_2 = quantile(datain2,0.75);
IQR_2 = Q3_2 - Q1_2;
DataLimLower_2 = Q1_2 - k * exp(-3.5 * MC_2) * IQR_2;
DataLimUpper_2 = Q3_2 + k * exp(4 * MC_2) * IQR_2;
% boxplot
boxplot([datain1,datain2],'Whisker',k,'Orientation',orientation,...
'OutlierSize',10,'Symbol','*r', ...
'labels',{'Normal(15,1)+outlier','Log-normal(0,1)+outlier'});
title({'Boxplot adjusted for skewness' , 'with medcouple (red limits)'}, 'FontSize' , 20)
set(gca,'FontSize',16);
switch orientation
case 'vertical'
% add the limits (for vertical boxplot)
xx = xlim(gca);
xx2 = xx/1.1; xx2(1) = xx(2)/1.5;
xx1 = xx/2; xx1(1) = xx(2)/3.5;
line(xx1,[DataLimLower_1 , DataLimLower_1] , 'Color','red');
line(xx1,[DataLimUpper_1 , DataLimUpper_1] , 'Color','red');
line(xx2,[DataLimLower_2 , DataLimLower_2] , 'Color','red');
line(xx2,[DataLimUpper_2 , DataLimUpper_2] , 'Color','red');
case 'horizontal'
% add the limits (for horizontal boxplot)
yy = ylim(gca);
yy2 = yy/1.1; yy2(1) = yy(2)/1.5;
yy1 = yy/2; yy1(1) = yy(2)/3.5;
line([DataLimLower_1 , DataLimLower_1] , yy1,'Color','red');
line([DataLimUpper_1 , DataLimUpper_1] , yy1,'Color','red');
line([DataLimLower_2 , DataLimLower_2] , yy2,'Color','red');
line([DataLimUpper_2 , DataLimUpper_2] , yy2,'Color','red');
end
Related Examples
 Assess the perfomance of the various medcouple solutions.
Assess the perfomance of the various medcouple solutions.
 Assess the perfomance of the various medcouple solutions.
Assess the perfomance of the various medcouple solutions.
% Uses the time execution of the weighted median returned in varargout
% Tm=matlab-fast-quickselectFSw; Tw=matlab-fast-whimed
% Ts=matlab-simplified; To=matlab-octile; Tq=matlab-quantiles;
tm=0; tmmex=0; tw=0; ts=0; to = 0; tq=0;
N = 800; % sample size
cycles = 1000; % number of repetitions
for c = 1:cycles
if mod(c,floor(cycles/10))==0, disp(['repetition n. ' num2str(c)]); end
% Generate different random sequences (seed 896 is a good one to
% compare consistency with the original C code on a difficult sequence)
myseed = randi(1000,1,1);
rng(myseed , 'twister');
datain = rand(N,1);
% REMARK: to generate N random integers (for example between 1 and
% 1000) using the Mersenne Twister in both C and MATLAB, note that the
% line below is equivalent to randi(1000,N,1):
%datain = ceil(datain*1000);
% Line below is to test with skewed data from the lognormal
%datain = lognrnd(0,1,N,1);
% just to ensure that data are stored in a column vector
datain = datain(:);
% $n\log n$, using quickselectFSw
tm0 = tic;
[MCm , t_diva] = medcouple(datain,0,0);
tm = tm+toc(tm0);
% $n\log n$, using quickselectFSwmex
tm0mex = tic;
[MCmmex , t_diva_mex] = medcouple(datain,0,2);
tmmex = tmmex+toc(tm0mex);
% $n\log n$, using Haase's weighted median (which is based on MATLAB sortrows)
tw0 = tic;
[MCw , t_Haase] = medcouple(datain,0,1);
tw = tw+toc(tw0);
% $n^2$ "naive" algorithm, simplified
ts0 = tic;
MCs = medcouple(datain,1);
ts = ts+toc(ts0);
% Quantiles-based approximation
to0 = tic;
MCo = medcouple(datain,2);
to = to+toc(to0);
% Octiles-based approximation
tq0 = tic;
MCq = medcouple(datain,3);
tq = tq+toc(tq0);
end
disp(' ');
disp(['OVERALL TIME EXECUTION IN ' num2str(cycles) ' MC COMPUTATION']);
disp(['time using WM by Haase = ' num2str(tw)]);
disp(['time using quickselectFSw = ' num2str(tm)]);
disp(['time using quickselectFSwmex = ' num2str(tmmex)]);
disp(['time using the naive = ' num2str(ts)]);
disp(['time using quantiles = ' num2str(tq)]);
disp(['time using octiles = ' num2str(to)]);
disp(' ');
disp('TIME SPENT IN COMPUTING WEIGHTED AVERAGES IN A SINGLE MC COMPUTATION')
disp(['t_Haase = ' num2str(t_Haase)]);
disp(['t_quickselectFSw = ' num2str(t_diva)]);
disp(['t_quickselectFSwmex = ' num2str(t_diva_mex)]);
repetition n. 100 repetition n. 200 repetition n. 300 repetition n. 400 repetition n. 500 repetition n. 600 repetition n. 700 repetition n. 800 repetition n. 900 repetition n. 1000 OVERALL TIME EXECUTION IN 1000 MC COMPUTATION time using WM by Haase = 0.88261 time using quickselectFSw = 0.53556 time using quickselectFSwmex = 0.34337 time using the naive = 1.6311 time using quantiles = 0.03368 time using octiles = 0.073907 TIME SPENT IN COMPUTING WEIGHTED AVERAGES IN A SINGLE MC COMPUTATION t_Haase = 0.0005846 t_quickselectFSw = 0.000214 t_quickselectFSwmex = 7.64e-05
Input Arguments
z — Uni-dimensional array.
The elements of the array z represent a
sample from a univariate distribution.
They can be missing (nan) of infinite (inf) values, which are excluded from the computation if present.
Data Types: single| double
Optional Arguments
mcm — Scalar.
Medcouple Method.
By default (mcm = 0 or not specified) the medcouple is computed using a fast algorithm.
mcm = 1 applies a naive O^2(n) method. With mcm = 2 the medcouple is replaced by a quantile-based approximation.
Similarily, mcm = 3 uses a octile-based approximation.
All methods are discussed in the references reported below. The fast options are the most precise; the simplified (naive) algotithm is also very fast but may be less accurate, as the kernel function of Hubert and Struyf is implemented in a way that does not take into account possible zeros at the denominator (these cases are simply not considered in the calculation). The quantile and octile approximations by definition are robust skewness estimators alternatives to the medcouple.
Example: 'mcm',2
Data Types: single | double
wmm — Scalar.
Weighted Median Method.
By default (wmm=0 or not specified) the weighted median is computed using function quickselectFSw, which csn compute any weighted quantile. If wmm=1 the weighted median is computed using the algorithm by Sven Haase https://it.mathworks.com/matlabcentral/fileexchange/23077-weighted-median Option wmm=2 applies the mex file quickselectFSwmex.
Example: 'wmm',1
Data Types: single | double
Output Arguments
varargout —T : The execution time spent for computing the weighted median.
Scalar
The computation of the weighted median is a critical step in the medcouple and it is also computational demanding.
For assessment purposes it is reported optionally.
More About
Additional Details
The fast algorithm for the medcouple (Brys G., Hubert M. and Struyf A., 2004) is a robust measure of skewness used to adjust the whiskers of a boxplot (Hubert M. and Vandervierenb E., 2008) and avoid wrong declaration of outliers in asymmetric univariate data. The medcouple replaces the classical skewness (that is based on the third moment of a data distribution) with a scaled median difference of the left and right half of the distribution. More precisely, it is defined as the median of the kernel function h(z_i,z_j)=\frac{(z_j-median(z))-(median(z)-z_i)}{z_j-z_i} over all pairs (z_i,z_j) where z_i<=median(z) and z_j >= median(z). The MATLAB toolbox LIBRA (https://wis.kuleuven.be/statdatascience/robust/LIBRA/) and the R package robustbase (https://cran.r-project.org/web/packages/robustbase) implement the fast medcouple with wrapper functions to the same compiled C source, to maximize speed. This medcouple function replicates faithfully the C function mlmc.c in pure MATLAB code, but replaces the key computations of the median and weighted median (which are intensively used) with calls to the FSDA functions quickselectFS and quickselectFSw or, optionally, to the n\log n solution of Sven Haase (2022) weightedMedian. The result is a readable MATLAB function that does not sacrifices performance. The FSDA implementation also optimizes the computation of the medcouple kernel function, to take into account the case where there are multiple values equal to the median, the denominator becomes 0 and the kernel is therefore defined differently: we computed it efficiently in the sub-function calwork, using the signum function. The consistency of the MATLAB and original C implementations have been carefully verified with simulations that ensure the same random numbers generation in the two environments. The code that has been used can be found in the FSDA github project.
References
Brys G., Hubert M. and Struyf A. (2004), A Robust Measure of Skewness, "Journal of Computational and Graphical Statistics", Vol. 13(4), pp. 996-1017.
Hubert M. and Vandervierenb E. (2008), An adjusted boxplot for skewed distributions, "Computational Statistics and Data Analysis", Vol. 52, pp. 5186-5201.
Johnson D.B. and Mizoguchi T. (1978), Selecting the Kth Element in X + Y and X1 + X2 + ... + Xm, "SIAM Journal of Computing", Vol. 7, pp. 147-153.
Hinkley D.V. (1975), On Power Transformations to Symmetry, "Biometrika", Vol. 62, pp.101-111.