restreigeneasy
restreigeneasy computes eigenvalues restriction (without Dykstra algorithm)
Syntax
Description
restreigeneasy restricts the eigenvalues according to the constraint specified in scalar restr. This function is a readable and understandble (but sometimes slower) version of routine restreigen.
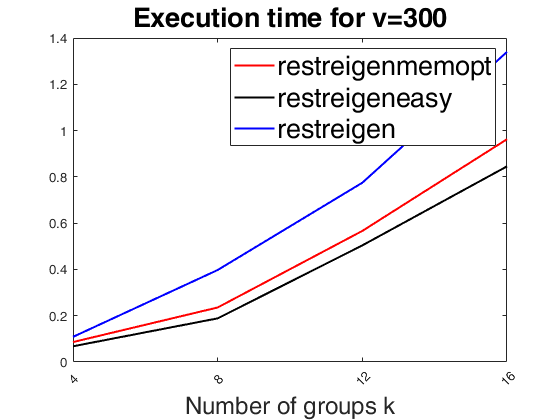
Computing time of three implementations of the eigenvalues restriction.out
=restreigeneasy(eigenvalues,
niini,
restr)
Examples
Related Examples
Input Arguments
Output Arguments
References
Fritz H., Garcia-Escudero, L.A. and Mayo-Iscar, A. (2013), A fast algorithm for robust constrained clustering, "Computational Satistics and Data Analysis", Vol. 61, pp. 124-136.
See Also
restreigen
|
tclust
|
restrdeter
|
tclustreg
 Computing time of three implementations of the eigenvalues restriction.
Computing time of three implementations of the eigenvalues restriction.