vervaatxdf
vervaatxdf returns the pdf and cdf of a Vervaat perpetuity.
Syntax
Description
The pdf and cdf of a Vervaat perpetuity with parameter \beta \in (0,+\infty), estimated following Barabesi and Pratelli (2019).
Examples
Input Arguments
Output Arguments
More About
References
Barabesi, L. and Pratelli, L. (2019), On the properties of a Takacs distribution, "Statistics and Probability Letters", Vol. 148, pp. 66-73.
Cloud, K. and Huber, M. (2018), Fast Perfect Simulation of Vervaat Perpetuities, "Journal of Complexity", Vol. 42, pp. 19-30.
Devroye, L. (2001), Simulating perpetuities, "Methodology And Computing In Applied Probability", Vol. 3, Num. 1, pp. 97-115.
Fill, J. A. and Huber, M. (2010), Perfect simulation of Vervaat perpetuities, "Electronic Journal of Probability", Vol. 15, pp. 96-109.
Devroye, L. and Fawzi, O. (2010), Simulating the Dickman distribution, "Statistics and Probability Letters", Vol. 80, pp. 242-247.
Blanchet, J. H. and Sigman, K. (2011), On exact sampling of stochastic perpetuities, "Journal of Applied Probability", Vol. 48A, pp. 165-182.
Takacs, L. (1955), On stochastic processes connected with certain physical recording apparatuses. "Acta Mathematica Academiae Scientificarum Hungarica", Vol. 6, pp 363-379.


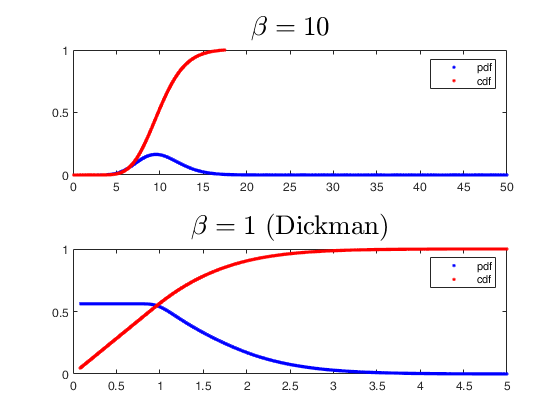
 Comparison of Vervaat perpetuities of different parameter values.
Comparison of Vervaat perpetuities of different parameter values.