wedgeplot

wedgeplot generates the double wedge plot of a time series

expand all in page

Syntax

Description

example

hf =wedgeplot(RES) Double wedge plot with simulated data with linear trend and level shift.

example

hf =wedgeplot(RES, Name, Value) Example of double wedge plot in series with level shift.

Examples

expand all

  • Double wedge plot with simulated data with linear trend and level shift.

    • No seasonal component. 

    pwd
    n=45;
    a=1;
    b=0.8;
    sig=1;
    seq=(1:n)';
    y=a+b*seq+sig*randn(n,1);
    y(round(n/2):end)=y(round(n/2):end)+10;
    % model with a quadratic trend, non seasonal and level shift
    model=struct;
    model.trend=2;
    model.seasonal=0;
    % Potential level shift position is investigated in positions:
    % t=10, t=11, ..., t=T-10.
    model.lshift=10:n-1;
    out=LTSts(y,'model',model);
    wedgeplot(out,'transpose',true,'extradata',[y out.yhat]);

  • Example of double wedge plot in series with level shift.

    • Analysis of contaminated airline data. 

    % Load the airline data.
    %   1949 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959 1960
    y = [112  115  145  171  196  204  242  284  315  340  360  417    % Jan
    118  126  150  180  196  188  233  277  301  318  342  391    % Feb
    132  141  178  193  236  235  267  317  356  362  406  419    % Mar
    129  135  163  181  235  227  269  313  348  348  396  461    % Apr
    121  125  172  183  229  234  270  318  355  363  420  472    % May
    135  149  178  218  243  264  315  374  422  435  472  535    % Jun
    148  170  199  230  264  302  364  413  465  491  548  622    % Jul
    148  170  199  242  272  293  347  405  467  505  559  606    % Aug
    136  158  184  209  237  259  312  355  404  404  463  508    % Sep
    119  133  162  191  211  229  274  306  347  359  407  461    % Oct
    104  114  146  172  180  203  237  271  305  310  362  390    % Nov
    118  140  166  194  201  229  278  306  336  337  405  432 ]; % Dec
    y=y(:);
    % Add a level shift contamintion plus some outliers.
    y(68:end)=y(68:end)+1300;
    y(67)=y(67)-600;
    y(45)=y(45)-800;
    y(68:69)=y(68:69)+800;
    % Create structure specifying model
    model=struct;
    model.trend=2;              % quadratic trend
    model.s=12;                 % monthly time series
    model.seasonal=204;         % number of harmonics
    model.lshift=40:120;        % position where to start monitoring level shift
    model.X='';
    % Create structure lts specifying lts options
    lts=struct;
    lts.bestr=20; % number of best solutions to bring to full convergence
    % h = dimension of the h subset (75 per cent of the data, bdp=0.25)
    h=round(0.75*length(y));
    [out, varargout]=LTSts(y,'model',model,'nsamp',500,...
    'lts',lts,'h',h,'plots',0,'msg',1);
    % Create the double wedge plot.
    wedgeplot(out);

    Related Examples

    expand all

  • Example of double wedge plot in series with level shift with option transpose.

    • Analysis of contaminated airline data. 

    % Load the airline data.
    %   1949 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959 1960.
    y = [112  115  145  171  196  204  242  284  315  340  360  417    % Jan
    118  126  150  180  196  188  233  277  301  318  342  391    % Feb
    132  141  178  193  236  235  267  317  356  362  406  419    % Mar
    129  135  163  181  235  227  269  313  348  348  396  461    % Apr
    121  125  172  183  229  234  270  318  355  363  420  472    % May
    135  149  178  218  243  264  315  374  422  435  472  535    % Jun
    148  170  199  230  264  302  364  413  465  491  548  622    % Jul
    148  170  199  242  272  293  347  405  467  505  559  606    % Aug
    136  158  184  209  237  259  312  355  404  404  463  508    % Sep
    119  133  162  191  211  229  274  306  347  359  407  461    % Oct
    104  114  146  172  180  203  237  271  305  310  362  390    % Nov
    118  140  166  194  201  229  278  306  336  337  405  432 ]; % Dec
    y=(y(:));
    % Add a level shift contamintion plus some outliers.
    y(50:55)=y(50:55)-300;
    y(68:end)=y(68:end)-700;
    y(70:75)=y(70:75)+300;
    y(90:90)=y(90:90)+300;
    % Create structure specifying model
    model=struct;
    model.trend=2;              % quadratic trend
    model.s=12;                 % monthly time series
    model.seasonal=204;         % number of harmonics
    model.lshift=40:120;        % position where to start monitoring level shift
    model.X='';
    % Create structure lts specifying lts options
    lts=struct;
    lts.bestr=20; % number of best solutions to bring to full convergence
    % h = dimension of the h subset (75 per cent of the data, bdp=0.25)
    [out, varargout]=LTSts(y,'model',model,'nsamp',500,...
    'lts',lts,'plots',0,'msg',1);
    % Create the double wedge plot.
    % Remember to remove the last column of the matrix of the residuals
    % obtained for each level shift position if you want to avoid the
    % top orange band (just execute RES(:,64)=[] before line 258).
    wedgeplot(out,'transpose',true,'extradata',[y out.yhat]);
    Level shift for t=40
Level shift for t=41
Level shift for t=42
Level shift for t=43
Level shift for t=44
Level shift for t=45
Level shift for t=46
Level shift for t=47
Level shift for t=48
Level shift for t=49
Level shift for t=50
Level shift for t=51
Level shift for t=52
Level shift for t=53
Level shift for t=54
Level shift for t=55
Level shift for t=56
Level shift for t=57
Level shift for t=58
Level shift for t=59
Level shift for t=60
Level shift for t=61
Level shift for t=62
Level shift for t=63
Level shift for t=64
Level shift for t=65
Level shift for t=66
Level shift for t=67
Level shift for t=68
Level shift for t=69
Level shift for t=70
Level shift for t=71
Level shift for t=72
Level shift for t=73
Level shift for t=74
Level shift for t=75
Level shift for t=76
Level shift for t=77
Level shift for t=78
Level shift for t=79
Level shift for t=80
Level shift for t=81
Level shift for t=82
Level shift for t=83
Level shift for t=84
Level shift for t=85
Level shift for t=86
Level shift for t=87
Level shift for t=88
Level shift for t=89
Level shift for t=90
Level shift for t=91
Level shift for t=92
Level shift for t=93
Level shift for t=94
Level shift for t=95
Level shift for t=96
Level shift for t=97
Level shift for t=98
Level shift for t=99
Level shift for t=100
Level shift for t=101
Level shift for t=102
Level shift for t=103
Level shift for t=104
Level shift for t=105
Level shift for t=106
Level shift for t=107
Level shift for t=108
Level shift for t=109
Level shift for t=110
Level shift for t=111
Level shift for t=112
Level shift for t=113
Level shift for t=114
Level shift for t=115
Level shift for t=116
Level shift for t=117
Level shift for t=118
Level shift for t=119
Level shift for t=120
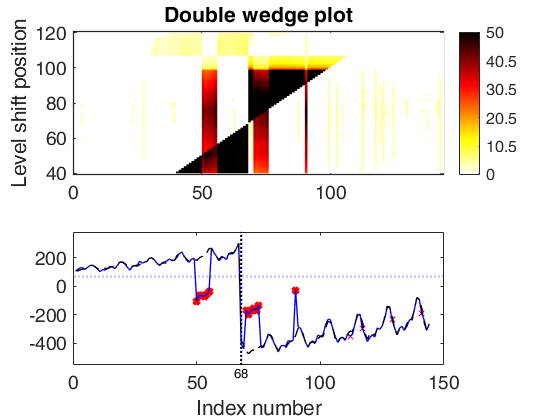
    Click here for the graphical output of this example (link to Ro.S.A. website)

  • Same double wedge plot as before, but with the time series at the top subplot.

    • This is obtained simply by specifying extradata before transpose. 

    % Load the airline data.
    %   1949 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959 1960.
    y = [112  115  145  171  196  204  242  284  315  340  360  417    % Jan
    118  126  150  180  196  188  233  277  301  318  342  391    % Feb
    132  141  178  193  236  235  267  317  356  362  406  419    % Mar
    129  135  163  181  235  227  269  313  348  348  396  461    % Apr
    121  125  172  183  229  234  270  318  355  363  420  472    % May
    135  149  178  218  243  264  315  374  422  435  472  535    % Jun
    148  170  199  230  264  302  364  413  465  491  548  622    % Jul
    148  170  199  242  272  293  347  405  467  505  559  606    % Aug
    136  158  184  209  237  259  312  355  404  404  463  508    % Sep
    119  133  162  191  211  229  274  306  347  359  407  461    % Oct
    104  114  146  172  180  203  237  271  305  310  362  390    % Nov
    118  140  166  194  201  229  278  306  336  337  405  432 ]; % Dec
    y=(y(:));
    % Add a level shift contamintion plus some outliers.
    y(50:55)=y(50:55)-300;
    y(68:end)=y(68:end)-700;
    y(70:75)=y(70:75)+300;
    y(90:90)=y(90:90)+300;
    % Create structure specifying model
    model=struct;
    model.trend=2;              % quadratic trend
    model.s=12;                 % monthly time series
    model.seasonal=204;         % number of harmonics
    model.lshift=40:120;        % position where to start monitoring level shift
    model.X='';
    % Create structure lts specifying lts options
    lts=struct;
    lts.bestr=20; % number of best solutions to bring to full convergence
    % h = dimension of the h subset (75 per cent of the data, bdp=0.25)
    [out, varargout]=LTSts(y,'model',model,'nsamp',500,...
    'lts',lts,'plots',0,'msg',1);
    % Create the double wedge plot.
    % Remember to remove the last column of the matrix of the residuals
    % obtained for each level shift position if you want to avoid the
    % top orange band (just execute RES(:,64)=[] before line 258).
    wedgeplot(out,'extradata',[y out.yhat],'transpose',true);

    Input Arguments

    expand all

    RES — absolute scaled residuals. Matrix or structure.

    Matrix of size T-by-(T-lshift) containing scaled residuals (in absolute value) for all the T units of the original time series monitored in steps lshift+1, lshift+2, ..., T-lshift, where lshift+1 is the first tentative level shift position, lshift +2 is the second level shift position, and so on. This matrix can be created by funtion LTSts (Least Trimmed Squares in time series). If RES is a structure, it must contain field:

    Value Description
    RES

    matrix containing scaled residuals.

    Data Types: double.

    Name-Value Pair Arguments

    Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

    Example: 'transpose',false , 'extradata', [y yhat] , 'cmapname','summer' , 'labls','Position of level shift' , 'labin','unit number' , 'titl','Plot with two wedges' , 'FontSize',12 , 'SizeAxesNum',10

    transpose —option determining the posiiton of the index number or tentative level shift.boolean.

    If transpose is true (default) the x-axis contains the tentative level shift position and the y-axis the index number else if it is false the axes are interchanged.

    When transpose is true, it is possible with option extradata to add on a separate panel a subplot of the original time series (and possibly the series of fitted values). See extradata option for details.

    Example: 'transpose',false

    Data Types: Boolean

    extradata —extra data to plot in a separate panel in association to the wedge plot.matrix.

    Matrix of size T-by-1 or T-by-p containing the data which have to be plotted in the separate panel.

    Generally extradata is a matrix of size T-by-2 containing the original time series and the corresponding fitted values in order to link the irregularities shown by the wedgeplot with the original time series.

    - If extradata is empty (default) the double wedge plot will be shown in a single panel.

    - If extradata is not empty a two panel plot will be created: one will contain the double wedge plot and extradata will be plot in the other panel. This options makes sense only if transpose is true, that is if the x axis of the double wedge plot contains the index number.

    When option transpose is left by the user unspecified, the default position of the extradata subplot is at the bottom.

    Otherwise, the position of the two panels depends on the order with which the user specifies the two options: if extradata is specified first, the corresponding subplot will be at the top, otherwse it will fall at the bottom.

    Example: 'extradata', [y yhat]

    Data Types: double

    cmapname —color map.character.

    Character which indicates the type of colormmap to use in the wedge plot. The accepted values are 'hot', 'autumn', 'spring', 'pink', 'summer', 'winter', 'gray'.

    The default is 'hot'.

    Example: 'cmapname','summer'

    Data Types: Character

    labls —label of the axis which contains the level shift position.character.

    Character containing the label to put on the axis which contains the level shift position. This axis could be either the horizontal or vertical depending on the option transpose. The default label is 'Tentative level shift position'.

    Example: 'labls','Position of level shift'

    Data Types: Character

    labin —label of the axis which contains the index number.character.

    Character containing the label to put on the axis which contains the index number of the units of the time series. This axis could be either the horizontal or vertical depending on the option transpose. The default label is 'Index number'.

    Example: 'labin','unit number'

    Data Types: Character

    titl —Title.string.

    A label for the title (default: 'Double wedge plot').

    Example: 'titl','Plot with two wedges'

    Data Types: char

    FontSize —Font size of the labels.scalar.

    Scalar which controls the font size of the labels of the axes and of the labels inside the plot. Default value is 12.

    Example: 'FontSize',12

    Data Types: double

    SizeAxesNum —Size of the numbers of the axis.scalar.

    Scalar which controls the size of the numbers of the axes. Default value is 12.

    Example: 'SizeAxesNum',10

    Data Types: double

    Output Arguments

    expand all

    hf —handle to the figure. Graphics handle

    Handle to the figure which has just been created.

    References

    Rousseeuw, P.J., Perrotta D., Riani M. and Hubert, M. (2018), Robust Monitoring of Many Time Series with Application to Fraud Detection, "Econometrics and Statistics". [RPRH]

    See Also

    This page has been automatically generated by our routine publishFS