MMmult

MMmult computes MM estimators in multivariate analysis with auxiliary S-scale

expand all in page

Syntax

Description

example

out =MMmult(Y) MMmult with all default options.

example

out =MMmult(Y, Name, Value) MMmult with optional arguments.

example

[out , varargout] =MMmult(___) MMmult with exctracted subsamples.

Examples

expand all

  • MMmult with all default options.

    • load('swiss_banknotes');
Y=swiss_banknotes{:,:};
Y=Y(1:100,:);
[n,v]=size(Y);
conflev=[0.95 0.99 1-0.01/n];
[outMM]=MMmult(Y);
malindexplot(outMM,v,'conflev',conflev);
ylabel('MM estimator')
    Total estimated time to complete S estimator:  0.65 seconds
    Click here for the graphical output of this example (link to Ro.S.A. website).

  • MMmult with optional arguments.

    • load('swiss_banknotes');
Y=swiss_banknotes{:,:};
Y=Y(1:100,:);
[out]=MMmult(Y,'plots',1);
    Total estimated time to complete S estimator:  0.24 seconds 
Warning: Matrix is close to singular or badly scaled. Results may be
inaccurate. RCOND =  5.683929e-18.
    Click here for the graphical output of this example (link to Ro.S.A. website).

  • MMmult with exctracted subsamples.

    • load('swiss_banknotes');
Y=swiss_banknotes{:,:};
Y=Y(1:100,:);
[outMM,C]=MMmult(Y);

    Input Arguments

    expand all

    Y — Input data. Matrix.

    n x v data matrix; n observations and v variables. Rows of Y represent observations, and columns represent variables.

    Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.

    Data Types: single|double

    Name-Value Pair Arguments

    Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

    Example: 'InitialEst',[] , 'Snsamp',1000 , 'Sbdp',0.4 , 'Sbestr',10 , 'Sminsctol',1e-7 , 'Snsamp',1000 , 'Srefsteps',0 , 'Sreftol',1e-8 , 'Srefstepsbestr',10 , 'Sreftolbestr',1e-10 , 'eff',0.99 , 'effshape',1 , 'refsteps',10 , 'tol',1e-10 , 'conflev',0.99 , 'plots',0 , 'nocheck',1 , 'ysave',1

    InitialEst —starting values of the MM-estimator.[] (default) | structure.

    InitialEst must contain the following fields:

    Value Description
    loc0

    1 x v vector (estimate of the centroid)
    shape0

    v x v matrix (estimate of the shape matrix)
    auxscale

    scalar (estimate of the scale parameter).

    If InitialEst is empty (default) program uses S estimators. In this last case it is possible to specify the options given in function Smult.

    Example: 'InitialEst',[]

    Data Types: struct

    Soptions —options if initial estimator is S and InitialEst is empty.sbestr, Sminsctol, Smsg, Snsamp, Srefsteps, Srefstepsbestr, Sreftol, Sreftolbestr, Srhofunc.

    .

    See function Smult for more details on these options.

    It is necessary to add to the S options the letter S at the beginning. For example, if you want to use the optimal rho function the supplied option is 'Srhofunc','optimal'. For example, if you want to use 3000 subsets, the supplied option is 'Snsamp',3000

    Example: 'Snsamp',1000

    Data Types: single | double

    Sbdp —breakdown point.scalar.

    It measures the fraction of outliers the algorithm should resist. In this case any value greater than 0 but smaller or equal than 0.5 will do fine (default=0.5).

    Note that given bdp nominal efficiency is automatically determined.

    Example: 'Sbdp',0.4

    Data Types: double

    Sbestr —number of "best betas" to remember.scalar.

    Scalar defining number of "best betas" to remember from the subsamples. These will be later iterated until convergence (default=5)

    Example: 'Sbestr',10

    Data Types: single | double

    Sminsctol —tolerance for the iterative procedure for finding the minimum value of the scale.scalar.

    Value of tolerance for the iterative procedure for finding the minimum value of the scale for each subset and each of the best subsets (It is used by subroutine minscale.m) The default value is 1e-7;

    Example: 'Sminsctol',1e-7

    Data Types: single | double

    Snsamp —Number of subsamples which will be extracted to find the robust estimator.scalar.

    If nsamp=0 all subsets will be extracted.

    They will be (n choose p).

    If the number of all possible subset is <1000 the default is to extract all subsets otherwise just 1000.

    Example: 'Snsamp',1000

    Data Types: single | double

    Srefsteps —Number of refining iterations.scalar.

    Number of refining iterationsin each subsample (default = 3).

    refsteps = 0 means "raw-subsampling" without iterations.

    Example: 'Srefsteps',0

    Data Types: single | double

    Sreftol —scalar.default value of tolerance for the refining steps.

    The default value is 1e-6;

    Example: 'Sreftol',1e-8

    Data Types: single | double

    Srefstepsbestr —number of refining iterations for each best subset.scalar.

    Scalar defining number of refining iterations for each best subset (default = 50).

    Example: 'Srefstepsbestr',10

    Data Types: single | double

    Sreftolbestr —Tolerance for the refining steps.scalar.

    Tolerance for the refining steps for each of the best subsets The default value is 1e-8;

    Example: 'Sreftolbestr',1e-10

    Data Types: single | double

    eff —nominal efficiency.scalar.

    Scalar defining nominal efficiency (i.e. a number between 0.5 and 0.99). The default value is 0.95 Asymptotic nominal efficiency is: $(\int \psi' d\Phi)^2 / (\psi^2 d\Phi)$

    Example: 'eff',0.99

    Data Types: double

    effshape —location or scale effiicency.dummy scalar.

    If effshape=1 efficiency refers to shape efficiency else (default) efficiency refers to location

    Example: 'effshape',1

    Data Types: double

    refsteps —Maximum iterations.scalar.

    Scalar defining maximum number of iterations in the MM loop. Default value is 100.

    Example: 'refsteps',10

    Data Types: double

    tol —Tolerance.scalar.

    Scalar controlling tolerance in the MM loop.

    Default value is 1e-7

    Example: 'tol',1e-10

    Data Types: double

    conflev —Confidence level which is used to declare units as outliers.scalar.

    Usually conflev=0.95, 0.975 0.99 (individual alpha) or 1-0.05/n, 1-0.025/n, 1-0.01/n (simultaneous alpha).

    Default value is 0.975

    Example: 'conflev',0.99

    Data Types: double

    plots —Plot on the screen.scalar | structure.

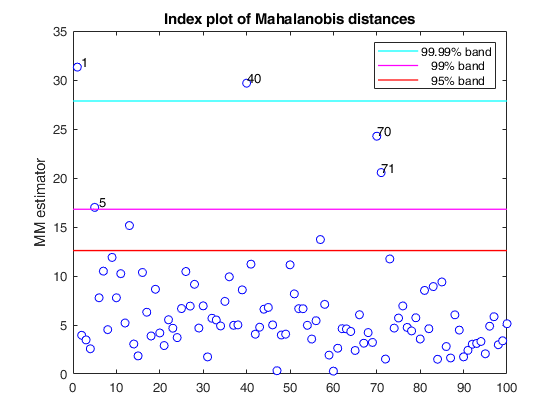
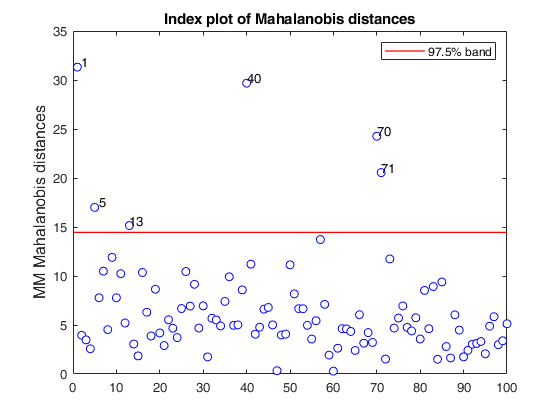
    If plots is a structure or scalar equal to 1, generates: (1) a plot of Mahalanobis distances against index number. The confidence level used to draw the confidence bands for the MD is given by the input option conflev. If conflev is not specified a nominal 0.975 confidence interval will be used.

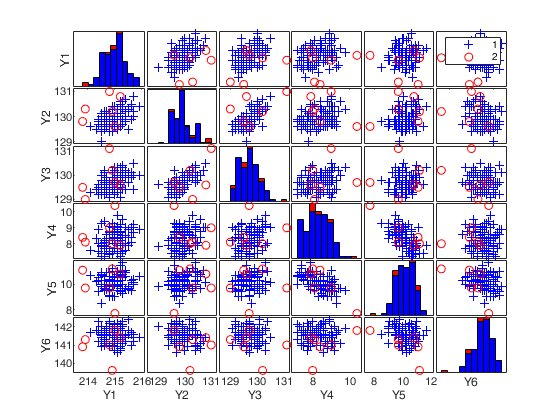
    (2) a scatter plot matrix with the outliers highlighted.

    If plots is a structure it may contain the following fields

    Value Description
    labeladd

    if this option is '1', the outliers in the spm are labelled with their unit row index. The default value is labeladd='', i.e. no label is added.
    nameY

    cell array of strings containing the labels of the variables. As default value, the labels which are added are Y1, ...Yv.

    Example: 'plots',0

    Data Types: single | double

    nocheck —Check input arguments.scalar.

    If nocheck is equal to 1 no check is performed on matrix Y. As default nocheck=0.

    Example: 'nocheck',1

    Data Types: double

    ysave —save input matrix Y.scalar.

    Scalar that is set to 1 to request that the data matrix Y is saved into the output structure out. This feature is meant at simplifying the use of function malindexplot.

    Default is 0, i.e. no saving is done.

    Example: 'ysave',1

    Data Types: double

    Output Arguments

    expand all

    out — description Structure

    A structure containing the following fields

    Value Description
    loc

    1 x v vector with MM estimate of location
    shape

    v x v matrix with MM estimate of the shape matrix
    cov

    v x v matrix with MM estimate of the covariance matrix Remark: covariance = auxscale^2 * shape
    weights

    n x 1 vector. Weights assigned to each observation
    outliers

    1 x k vectors containing the outliers which have been found
    Sloc

    1 x v vector with S estimate of location
    Sshape

    v x v matrix with S estimate of the shape matrix
    Scov

    v x v matrix with S estimate of the covariance matrix
    auxscale

    scalar, S estimate of the scale
    Y

    Data matrix Y. The field is present only if option ysave is set to 1.
    conflev

    scalar, confidence level which has been used
    md

    n x 1 vector containing robust Mahalanobis distances (in squared units).
    class

    'MMmult'

    varargout —Indices of the subsamples extracted for computing the estimate (the so called elemental sets). C : matrix

    References

    Maronna, R.A., Martin D. and Yohai V.J. (2006), "Robust Statistics, Theory and Methods", Wiley, New York.

    Acknowledgements

    This function follows the lines of MATLAB/R code developed during the years by many authors.

    For more details see the R library robustbase http://robustbase.r-forge.r-project.org/ The core of these routines, e.g. the resampling approach, however, has been completely redesigned, with considerable increase of the computational performance.

    See Also

    This page has been automatically generated by our routine publishFS