TBrho
TBrho computes rho function for Tukey's biweight
Syntax
rhoTB=TBrho(u,c)example
Examples
Related Examples
Input Arguments
Output Arguments
More About
References
Maronna, R.A., Martin D. and Yohai V.J. (2006), "Robust Statistics, Theory and Methods", Wiley, New York.
Riani, M., Cerioli, A. and Torti, F. (2014), On consistency factors and efficiency of robust S-estimators, "TEST", Vol. 23, pp. 356-387.
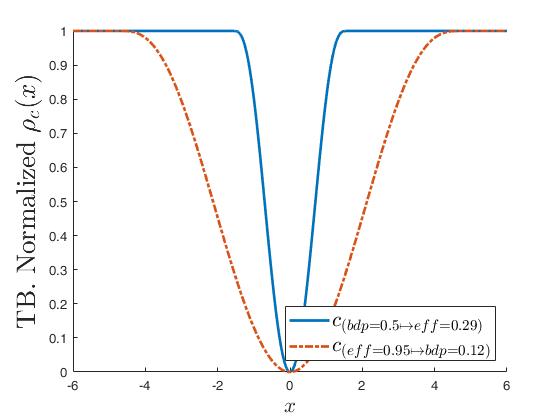
 Compare two rho functions for 2 different values of c.
Compare two rho functions for 2 different values of c.