FSRedaCens

FSRedaCens enables to monitor several quantities in each step of the forward search

expand all in page

Syntax

out=FSRedaCens(y,X,bsb)example
out=FSRedaCens(y,X,bsb,Name,Value)example

Description

example

out =FSRedaCens(y, X, bsb) FSRedaCens with all default options.

example

out =FSRedaCens(y, X, bsb, Name, Value) FSRedaCens with optional argument.

Examples

expand all

FSRedaCens with all default options.

Example of use of FSRedaCens based on a starting point coming from LMS.

n=200;
p=3;
rng default
rng(123456)
X=randn(n,p);
% Uncontaminated data
y=randn(n,1)+1;
% Contaminated data
ycont=y;
cont=1:5;
ycont(cont)=ycont(cont)+5;
ycont(ycont<=0)=0;
[out]=LXS(ycont,X,'nsamp',1000);
out=FSRedaCens(ycont,X,out.bs);
fground=struct;
fground.funit=cont;
resfwdplot(out,'fground',fground)

FSRedaCens with optional argument.

Example of use of function FSReda using a random start and traditional t-stat monitoring.

n=200;
p=3;
rng default
rng(123456)
X=randn(n,p);
% Uncontaminated data
y=randn(n,1);
% Contaminated data
ycont=y;
ycont(1:5)=ycont(1:5)+6;
ycont(ycont<=0)=0;
out=FSRedaCens(ycont,X,0,'tstat','trad');

Related Examples

expand all

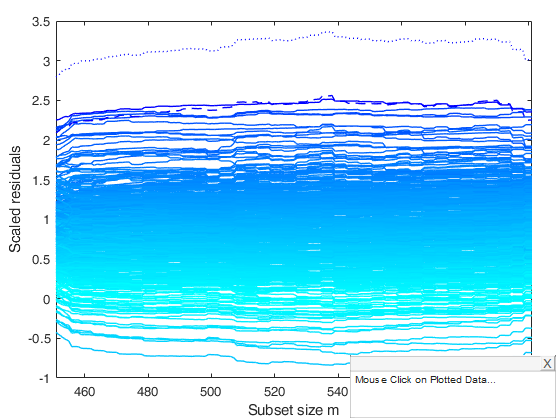
Monitoring of residuals using the affairs dataset.

In the example of Kleiber and Zeileis (2008, p. 142), the number of a person's extramarital sexual inter-courses ("affairs") in the past year is regressed on the person's age, number of years married, religiousness, occupation, and won rating of the marriage. The dependent variable is left-censored at zero and not right-censored. Hence this is a standard Tobit model which can be estimated by the following lines

load affairs.mat
X=affairs{:,["age" "yearsmarried" "religiousness" "occupation" "rating"]};
y=affairs{:,"affairs"};
outLXS=LXS(y,X);
[~,sor]=sort(abs(outLXS.residuals))
out=FSRedaCens(y,X,sor(1:100));
resfwdplot(out)

Total estimated time to complete LMS:  0.05 seconds 
Attention: there was an exact fit. Robust estimate of s^2 is <1e-7

sor =

     1
     2
     3
     4
     5
     6
     7
     8
     9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    87
    88
    89
    90
    91
    92
    93
    94
    95
    96
    97
    98
    99
   100
   101
   102
   103
   104
   105
   106
   107
   108
   109
   110
   111
   112
   113
   114
   115
   116
   117
   118
   119
   120
   121
   122
   123
   124
   125
   126
   127
   128
   129
   130
   131
   132
   133
   134
   135
   136
   137
   138
   139
   140
   141
   142
   143
   144
   145
   146
   147
   148
   149
   150
   151
   152
   153
   154
   155
   156
   157
   158
   159
   160
   161
   162
   163
   164
   165
   166
   167
   168
   169
   170
   171
   172
   173
   174
   175
   176
   177
   178
   179
   180
   181
   182
   183
   184
   185
   186
   187
   188
   189
   190
   191
   192
   193
   194
   195
   196
   197
   198
   199
   200
   201
   202
   203
   204
   205
   206
   207
   208
   209
   210
   211
   212
   213
   214
   215
   216
   217
   218
   219
   220
   221
   222
   223
   224
   225
   226
   227
   228
   229
   230
   231
   232
   233
   234
   235
   236
   237
   238
   239
   240
   241
   242
   243
   244
   245
   246
   247
   248
   249
   250
   251
   252
   253
   254
   255
   256
   257
   258
   259
   260
   261
   262
   263
   264
   265
   266
   267
   268
   269
   270
   271
   272
   273
   274
   275
   276
   277
   278
   279
   280
   281
   282
   283
   284
   285
   286
   287
   288
   289
   290
   291
   292
   293
   294
   295
   296
   297
   298
   299
   300
   301
   302
   303
   304
   305
   306
   307
   308
   309
   310
   311
   312
   313
   314
   315
   316
   317
   318
   319
   320
   321
   322
   323
   324
   325
   326
   327
   328
   329
   330
   331
   332
   333
   334
   335
   336
   337
   338
   339
   340
   341
   342
   343
   344
   345
   346
   347
   348
   349
   350
   351
   352
   353
   354
   355
   356
   357
   358
   359
   360
   361
   362
   363
   364
   365
   366
   367
   368
   369
   370
   371
   372
   373
   374
   375
   376
   377
   378
   379
   380
   381
   382
   383
   384
   385
   386
   387
   388
   389
   390
   391
   392
   393
   394
   395
   396
   397
   398
   399
   400
   401
   402
   403
   404
   405
   406
   407
   408
   409
   410
   411
   412
   413
   414
   415
   416
   417
   418
   419
   420
   421
   422
   423
   424
   425
   426
   427
   428
   429
   430
   431
   432
   433
   434
   435
   436
   437
   438
   439
   440
   441
   442
   443
   444
   445
   446
   447
   448
   449
   450
   451
   456
   457
   462
   470
   471
   473
   478
   479
   480
   483
   484
   491
   495
   500
   504
   506
   507
   508
   515
   521
   524
   529
   530
   534
   536
   544
   546
   567
   576
   578
   580
   581
   597
   601
   460
   492
   513
   517
   522
   543
   554
   558
   561
   566
   569
   571
   575
   582
   586
   599
   600
   452
   453
   461
   467
   476
   481
   482
   501
   510
   520
   525
   539
   540
   563
   577
   584
   585
   589
   595
   454
   459
   463
   468
   469
   472
   477
   485
   486
   487
   489
   490
   498
   499
   503
   505
   509
   511
   512
   514
   516
   518
   519
   527
   528
   532
   533
   545
   549
   552
   557
   560
   562
   570
   573
   574
   583
   590
   591
   593
   596
   598
   455
   458
   464
   465
   466
   474
   475
   488
   493
   494
   496
   497
   502
   523
   526
   531
   535
   537
   538
   541
   542
   547
   548
   550
   551
   553
   555
   556
   559
   564
   565
   568
   572
   579
   587
   588
   592
   594

m=100
m=200
m=300
m=400
m=500
m=600

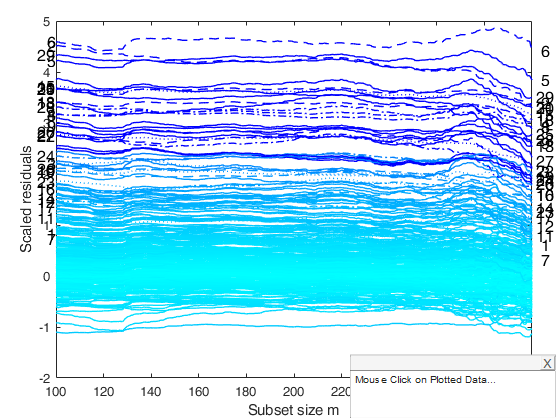
Click here for the graphical output of this example (link to Ro.S.A. website)

Outliers and a Lower Threshold example.

rng default
rng(2)
n=300;
lambda=-0.5;
p=5;
sigma=0.1;
beta=1*ones(p,1);
X=0.2*randn(n,p);
epsilon=randn(n,1);
y=X*beta+sigma*epsilon;
y=normYJ(y,1,lambda,'inverse',true,'Jacobian',false);
sel=1:30;
y(sel)=y(sel)+1.2;
qq=quantile(y,0.3);
y(y<=qq)=qq;
left=min(y);
right=Inf;
% See function FSRfanCens on the procedure to find the correct
% transformation
yf=normYJ(y,1,lambda,'inverse',false,'Jacobian',false);
leftf=normYJ(left,1,lambda,'inverse',false,'Jacobian',false);
rightf=normYJ(right,1,lambda,'inverse',false,'Jacobian',false);
zlimits=[leftf rightf];
% Call to FSRedaCens
outLXS=LXS(yf,X);
out=FSRedaCens(yf,X,outLXS.bs,'left',leftf,'right',rightf,'init',100);
fground.funit=1:30;
resfwdplot(out,'fground',fground);

Total estimated time to complete LMS:  0.03 seconds 
m=100
m=200
m=300

Input Arguments

expand all

`y` — Response variable. Vector.

Response variable, specified as a vector of length n, where n is the number of observations. Each entry in y is the response for the corresponding row of X.

Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.

Data Types: single| double

`X` — Data matrix of explanatory variables (also called 'regressors') of dimension (n x p-1). Rows of X represent observations, and columns represent variables.

Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.

Data Types: single| double

`bsb` — list of units forming the initial subset. Vector or scalar.

If bsb=0 (default), then the procedure starts with p units randomly chosen, else if bsb is not 0, the search will start with m0=length(bsb).

Data Types: single| double

Name-Value Pair Arguments

Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

Example:

 'balancedSearch',false
, 'conflev',[0.90 0.93]
, 'init',100 starts monitoring from step m=100
, 'left',1
, 'intercept',false
, 'nocheck',true
, 'right',800
, 'tstat','trad'

`balancedSearch` —Balanced search.scalar logical.

If Balanced search the proportion of observations in the subsets equals (as much as possible) the proportion of units in the sample. The default value of balancedSearch is true.

Example: 'balancedSearch',false

Data Types: logical

`conflev` —confidence levels to be used to compute confidence interval for the elements of $\beta$ and for $\sigma^2$.vector.

The default value of conflev is [0.95 0.99] that is 95% and 99% confidence intervals are computed.

Example: 'conflev',[0.90 0.93]

Data Types: double

`init` —Search initialization.scalar.

It specifies the point where to initialize the search and start monitoring required diagnostics. If init is not specified it will be set equal to : p+1, if the sample size is smaller than 40;

min(3*p+1,floor(0.5*(n+p+1))), otherwise.

Example: 'init',100 starts monitoring from step m=100

Data Types: double

`left` —left limit for the censored dependent variable.scalar.

If set to -Inf, the dependent variable is assumed to be not left-censored; default value of left is zero (classical Tobit model).

Example: 'left',1

Data Types: double

`intercept` —Indicator for constant term.true (default) | false.

Indicator for the constant term (intercept) in the fit, specified as the comma-separated pair consisting of 'Intercept' and either true to include or false to remove the constant term from the model.

Example: 'intercept',false

Data Types: boolean

`nocheck` —Check input arguments.boolean.

If nocheck is equal to true, no check is performed on matrix y and matrix X. Notice that y and X are left unchanged. In other words the additional column of ones for the intercept is not added. As default nocheck=false. The controls on h, alpha and nsamp still remain

Example: 'nocheck',true

Data Types: boolean

`right` —right limit for the censored dependent variable.scalar.

If set to Inf, the dependent variable is assumed to be not right-censored; default value of right is Inf (classical Tobit model).

Example: 'right',800

Data Types: double

`tstat` —the kind of t-statistics which have to be monitored.character.

tstat = 'trad' implies monitoring of traditional t statistics (out.Tols). In this case the estimate of $\sigma^2$ at step m is based on $s^2_m$ (notice that $s^2_m<<\sigma^2$ when m/n is small) tstat = 'scal' (default) implies monitoring of rescaled t statistics In this case the estimate of $\sigma^2$ at step m is based on $s^2_m / var_{truncnorm(m/n)}$ where $var_{truncnorm(m/n)}$ is the variance of the truncated normal distribution.

Example: 'tstat','trad'

Data Types: char

Output Arguments

expand all

`out` — description Structure

Structure which contains the following fields

Value	Description
`RES`	n x (n-init+1) = matrix containing the monitoring of scaled residuals: 1st row = residual for first unit; ...; nth row = residual for nth unit.
`LEV`	(n+1) x (n-init+1) = matrix containing the monitoring of leverage: 1st row = leverage for first unit: ...; nth row = leverage for nth unit.
`BB`	n x (n-init+1) matrix containing the information about the units belonging to the subset at each step of the forward search: 1st col = indexes of the units forming subset in the initial step; ...; last column = units forming subset in the final step (all units).
`mdr`	n-init x 3 matrix which contains the monitoring of minimum deletion residual or (m+1)ordered residual at each step of the forward search: 1st col = fwd search index (from init to n-1); 2nd col = minimum deletion residual; 3rd col = (m+1)-ordered residual. Remark: these quantities are stored with sign, that is the min deletion residual is stored with negative sign if it corresponds to a negative residual.
`msr`	n-init+1 x 3 = matrix which contains the monitoring of maximum studentized residual or m-th ordered residual: 1st col = fwd search index (from init to n); 2nd col = maximum studentized residual; 3rd col = (m)-ordered studentized residual.
`nor`	(n-init+1) x 4 matrix containing the monitoring of normality test in each step of the forward search: 1st col = fwd search index (from init to n); 2nd col = Asymmetry test; 3rd col = Kurtosis test; 4th col = Normality test.
`Bols`	(n-init+1) x (p+1) matrix containing the monitoring of estimated beta coefficients in each step of the forward search.
`S2`	(n-init+1) x 5 matrix containing the monitoring of S2 or R2, F test, in each step of the forward search: 1st col = fwd search index (from init to n); 2nd col = monitoring of S2; 3rd col = monitoring of R2; 4th col = monitoring of rescaled S2. In this case the estimated of $\sigma^2$ at step m is divided by the consistency factor (to make the estimate asymptotically unbiased). 5th col = monitoring of F test. Note that an asymptotic unbiased estimate of sigma2 is used.
`coo`	(n-init+1) x 3 matrix containing the monitoring of Cook or modified Cook distance in each step of the forward search: 1st col = fwd search index (from init to n); 2nd col = monitoring of Cook distance; 3rd col = monitoring of modified Cook distance.
`Tols`	(n-init+1) x (p+1) matrix containing the monitoring of estimated t-statistics (as specified in option input 'tstat'. in each step of the forward search
`Un`	(n-init) x 11 Matrix which contains the unit(s) included in the subset at each step of the fwd search. REMARK: in every step the new subset is compared with the old subset. Un contains the unit(s) present in the new subset but not in the old one. Un(1,2), for example, contains the unit included in step init+1. Un(end,2) contains the units included in the final step of the search.
`betaINT`	Confidence intervals for the elements of $\beta$. betaINT is a (n-init+1)-by-2*length(confint)-by-p 3D array. Each third dimension refers to an element of beta: betaINT(:,:,1) is associated with first element of beta; ...; betaINT(:,:,p) is associated with last element of beta. The first two columns contain the lower and upper confidence limits associated with conflev(1). Columns three and four contain the lower and upper confidence limits associated with conflev(2); ...; The last two columns contain the lower and upper confidence limits associated with conflev(end). For example, betaint(:,3:4,5) contain the lower and upper confidence limits for the fifth element of beta using confidence level specified in the second element of input option conflev.
`sigma2INT`	confidence interval for $\sigma^2$. 1st col = fwd search index; 2nd col = lower confidence limit based on conflev(1); 3rd col = upper confidence limit based on conflev(1); 4th col = lower confidence limit based on conflev(2); 5th col = upper confidence limit based on conflev(2); ... penultimate col = lower confidence limit based on conflev(end); last col = upper confidence limit based on conflev(end);
`y`	A vector with n elements that contains the response variable which has been used
`X`	Data matrix of explanatory variables which has been used (it also contains the column of ones if input option intercept was missing or equal to 1)
`class`	'FSReda'.

References

Atkinson, A.C. and Riani, M. (2000), "Robust Diagnostic Regression Analysis", Springer Verlag, New York.

Documentation

FSRedaCens

Syntax

Description

Examples

FSRedaCens with all default options.

FSRedaCens with optional argument.

Related Examples

Monitoring of residuals using the affairs dataset.

Outliers and a Lower Threshold example.

Input Arguments

`y` — Response variable. Vector.

`X` — Data matrix of explanatory variables (also called 'regressors') of dimension (n x p-1). Rows of X represent observations, and columns represent variables.

`bsb` — list of units forming the initial subset. Vector or scalar.

Name-Value Pair Arguments

`balancedSearch` —Balanced search.scalar logical.

`conflev` —confidence levels to be used to compute confidence interval for the elements of $\beta$ and for $\sigma^2$.vector.

`init` —Search initialization.scalar.

`left` —left limit for the censored dependent variable.scalar.

`intercept` —Indicator for constant term.true (default) | false.

`nocheck` —Check input arguments.boolean.

`right` —right limit for the censored dependent variable.scalar.

`tstat` —the kind of t-statistics which have to be monitored.character.

Output Arguments

`out` — description Structure

References

See Also

Documentation

FSRedaCens

Syntax

Description

Examples

FSRedaCens with all default options.

FSRedaCens with optional argument.

Related Examples

Monitoring of residuals using the affairs dataset.

Outliers and a Lower Threshold example.

Input Arguments

y — Response variable. Vector.

X — Data matrix of explanatory variables (also called 'regressors') of dimension (n x p-1). Rows of X represent observations, and columns represent variables.

bsb — list of units forming the initial subset. Vector or scalar.

Name-Value Pair Arguments

balancedSearch —Balanced search.scalar logical.

conflev —confidence levels to be used to compute confidence interval for the elements of $\beta$ and for $\sigma^2$.vector.

init —Search initialization.scalar.

left —left limit for the censored dependent variable.scalar.

intercept —Indicator for constant term.true (default) | false.

nocheck —Check input arguments.boolean.

right —right limit for the censored dependent variable.scalar.

tstat —the kind of t-statistics which have to be monitored.character.

Output Arguments

out — description Structure

References

See Also

`y` — Response variable. Vector.

`X` — Data matrix of explanatory variables (also called 'regressors') of dimension (n x p-1). Rows of X represent observations, and columns represent variables.

`bsb` — list of units forming the initial subset. Vector or scalar.

`balancedSearch` —Balanced search.scalar logical.

`conflev` —confidence levels to be used to compute confidence interval for the elements of $\beta$ and for $\sigma^2$.vector.

`init` —Search initialization.scalar.

`left` —left limit for the censored dependent variable.scalar.

`intercept` —Indicator for constant term.true (default) | false.

`nocheck` —Check input arguments.boolean.

`right` —right limit for the censored dependent variable.scalar.

`tstat` —the kind of t-statistics which have to be monitored.character.

`out` — description Structure