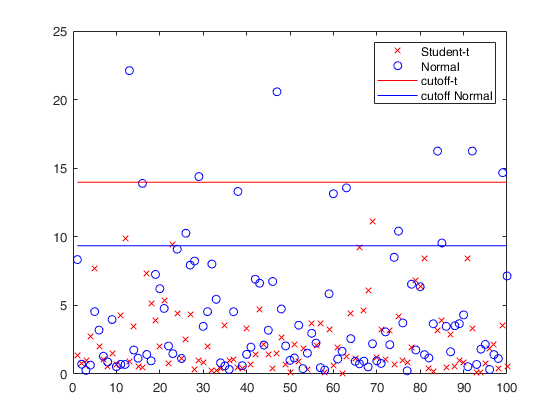
msdcutoff
Mahalanobis Squared Distance cutoff
Description
Examples
Related Examples
Input Arguments
Output Arguments
More About
References
Gnanadesikan, R. and Kettenring, J. R. (1972), Robust estimates, residuals, and outlier detection with multiresponse data. Biometrics, 28:81–124.
Barabesi, L. and Cerioli, A. and García-Escudero, L.A. and Mayo-Iscar, A. (2023), Trimming heavy-tailed multivariate data. Submitted.
Mardia, K. and Kent, J. and Bibby, J. (1979), Multivariate Analysis, Academic Press, New York.
Rousseeuw, P.J. and Van Driessen, K. (1999), A fast algorithm for the minimum covariance determinant estimator, Technometrics, 41:212-223.
Maronna, R.A., Martin D. and Yohai V.J. (2006), "Robust Statistics, Theory and Methods", Wiley, New York.
 cutoff values for robust squared Mahalanobis distances.
cutoff values for robust squared Mahalanobis distances.