ASc
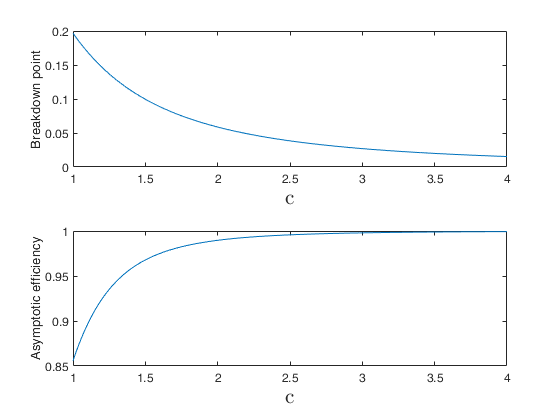
ASc computes breakdown point and efficiency associated with constant c for Andrew's rho function
Description
Examples
Related Examples
Breakdown vs efficiency.
Breakdown vs efficiency.
%% Breakdown vs efficiency.
%Analysis of breakdown point and asymptotic efficiency
%at the normal distribution as a function of c in regression.
c=1:0.01:4;
CC=[c' zeros(length(c),1)];
jk=0;
for j=c
jk=jk+1;
[bdp,eff]=ASc(j,1);
CC(jk,2:3)=[bdp,eff];
end
subplot(2,1,1)
plot(c',CC(:,2))
xlabel('c','Interpreter','Latex','FontSize',16)
ylabel('Breakdown point','Interpreter','none')
subplot(2,1,2)
plot(c',CC(:,3))
xlabel('c','Interpreter','Latex','FontSize',16)
ylabel('Asymptotic efficiency','Interpreter','none')
Input Arguments
Output Arguments
More About
References
Andrews, D.F., Bickel, P.J., Hampel, F.R., Huber, P.J., Rogers, W.H., and Tukey, J.W. (1972), "Robust Estimates of Location: Survey and Advances", Princeton Univ. Press, Princeton, NJ. [p. 203]
Andrews, D. F. (1974). A Robust Method for Multiple Linear Regression, "Technometrics", V. 16, pp. 523-531, https://doi.org/10.1080/00401706.1974.10489233
Riani, M., Cerioli, A. and Torti, F. (2014), On consistency factors and efficiency of robust S-estimators, "TEST", Vol. 23, pp. 356-387.