Scalar greater than 0 which
controls the robustness/efficiency of the estimator
Data Types: single| double
Number of variables of
the dataset (for regression v=1)
UP TO NOW v=1 (JUST REGRESSION) TO DO FOR MULTIVARIATE
ANALYSIS
Data Types: single| double
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
Example:
'param',[1.5,3.5,8]
, 'shapeeff',1
Vector of length 3 specifying the
parameters a, b and c of the weight function of the Hampel
estimator.
param(1)=a param(2)=b param(3)=c
If these values are not supplied they will be automatically
set to a=2, b=4 c=8
Example: 'param',[1.5,3.5,8]
Data Types: double
If 1, the efficiency
is referred to the shape else (default) is referred to the
location. TODO:Hac:shapeeff
Example: 'shapeeff',1
Data Types: double
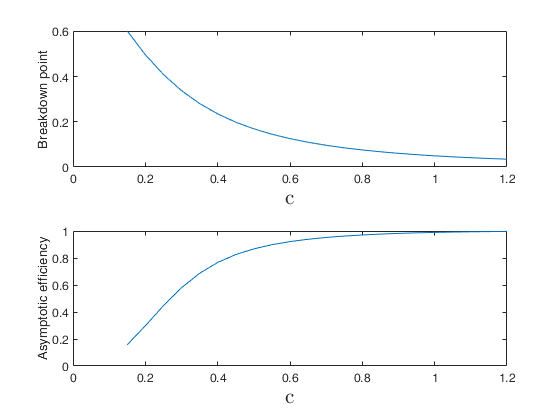
 bdp and eff as function of c.
bdp and eff as function of c.