OPTc
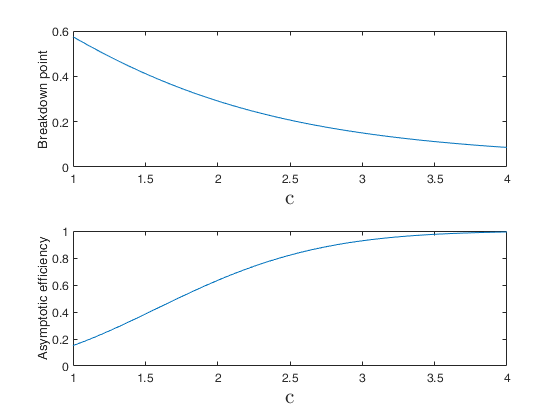
OPTc computes breakdown point and efficiency associated with constant c for Optimal rho function
Syntax
Description
Examples
Input Arguments
Output Arguments
More About
References
Maronna, R.A., Martin D. and Yohai V.J. (2006), "Robust Statistics, Theory and Methods", Wiley, New York.
 Breakdown vs efficiency.
Breakdown vs efficiency.