ASpsider
ASpsider computes derivative of psi function (second derivative of rho function) for Andrew's sine function
Syntax
psiderAS=ASpsider(u,c)example
Description
Examples
Input Arguments
Output Arguments
More About
References
Andrews, D.F., Bickel, P.J., Hampel, F.R., Huber, P.J., Rogers, W.H., and Tukey, J.W. (1972), "Robust Estimates of Location: Survey and Advances", Princeton Univ. Press, Princeton, NJ. [p. 203]
Andrews, D. F. (1974). A Robust Method for Multiple Linear Regression, "Technometrics", V. 16, pp. 523-531, https://doi.org/10.1080/00401706.1974.10489233
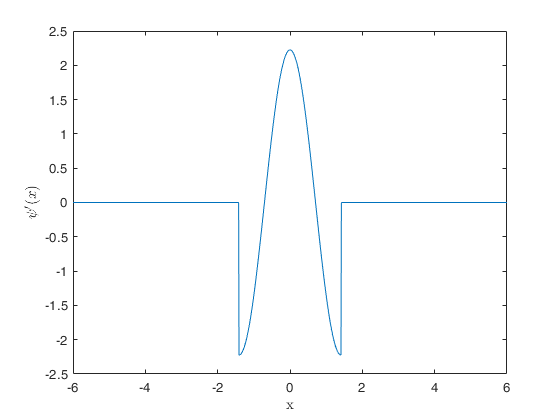
 Plot the derivative of Andrew's psi function (when bdp=0.5).
Plot the derivative of Andrew's psi function (when bdp=0.5).