ASrho
ASrho computes rho function for Andrew's sine function
Syntax
rhoAS=ASrho(u,c)example
Examples
Related Examples
Input Arguments
Output Arguments
More About
References
Andrews, D.F., Bickel, P.J., Hampel, F.R., Huber, P.J., Rogers, W.H., and Tukey, J.W. (1972), "Robust Estimates of Location: Survey and Advances", Princeton Univ. Press, Princeton, NJ. [p. 203]
Andrews, D. F. (1974). A Robust Method for Multiple Linear Regression, "Technometrics", V. 16, pp. 523-531, https://doi.org/10.1080/00401706.1974.10489233

|
ASpsix |
ASwei |
 |
|
|
Functions |
|
• The developers of the toolbox • The forward search group • Terms of Use • Acknowledgments
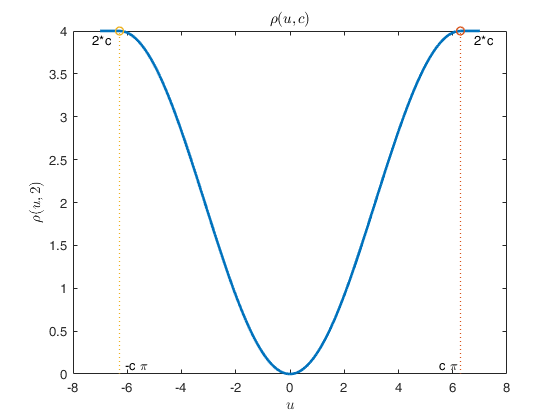
 Plot of rho function.
Plot of rho function.