FNChygernd
FNChygernd random arrays from the Fisher non central hypergeometric distribution.
Syntax
Description
Generate a random number from Wallenius non central hypergeometric distribution.r
=FNChygernd(M,
K,
n,
odds)
Examples
Related Examples
Input Arguments
Output Arguments
References
Fog, A. (2008), Calculation Methods for Wallenius' Noncentral Hypergeometric Distribution, "Communications in Statistics - Simulation and Computation", Vol. 37, pp. 258-273.
See Also
FNChygepdf
|
FNChygecdf
|
FNChygeinv
|
WNChygernd
|
WNChygepdf
|
WNChygecdf
|
WNChygeinv
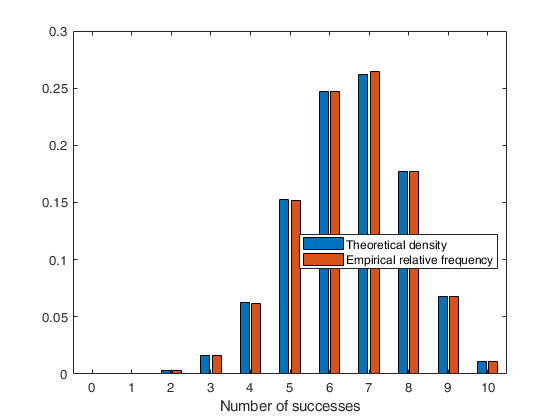
 Comparison density and relatived frequencies based on random numbers.
Comparison density and relatived frequencies based on random numbers.