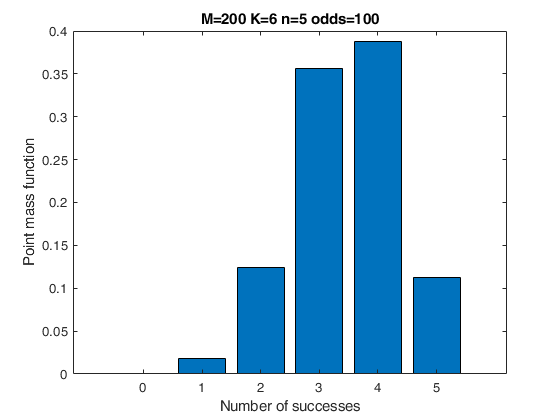
WNChygepdf

WNChygepdf returns Wallenius' non-central hypergeometric probability density function

Syntax

Wpdf=WNChygepdf(x,M,K,n,odds)example
Wpdf=WNChygepdf(x,M,K,n,odds, accuracy)example

Description

This function calls function WalleniusNCHypergeometricpdf which is a translation into MATLAB of the corresponding C++ function of Fog (2008).

The notation which is used in WNChygepdf and the order of the arguments is the one of MATLAB hyge. The notation which is used inside WalleniusNCHypergeometricpdf is the original one of Fog.

To illustrate the meaning of Wallenius and Fisher' function parameters, let's use the classical biased urn example, with $K$ red balls and $M-K$ white balls, totalling $M$ balls. $n$ balls are drawn at random from the urn without replacement. Each red ball has the weight $\omega_{1}$, and each white ball has the weight $\omega_{2}$; the probability ratio of red over white balls is then given by $odds = \omega_{1} / \omega_{2}$. Note that the odds are fixed once and for all during the drawings.

If the balls are taken one by one, the probability (say $p_1$) that the first ball picked is red is equal to the weight fraction of red balls:

\[ p_1= \frac{K w_1}{K w_1 + (M-K) w_2} \]

In the Wallenius distribution the probability that the second ball picked is red depends on whether the first ball was red or white. If the first ball was red then the above formula is used with $K$ reduced by one. If the first ball was not red then the above formula is used with $M-K$ reduced by one. The number of red balls that we get in this experiment is a random variable with Wallenius' noncentral hypergeometric distribution.

The important fact that distinguishes Wallenius' distribution is that there is competition between the balls. The probability that a particular ball is taken in a particular draw depends not only on its own weight, but also on the total weight of the competing balls that remain in the urn at that moment. And the weight of the competing balls depends on the outcomes of all preceding draws. In the Fisher model, the fates of the balls are independent and there is no dependence between draws. One may as well take all $n$ balls at the same time. Each ball has no "knowledge" of what happens to the other balls.

More formally, if the total number $n$ of balls taken is known then the conditional distribution of the number of taken red balls for given $n$ is Fisher's noncentral hypergeometric distribution.

These two distributions have important applications in evolutionary biology and population genetics. If animals of a particular species are competing for a limited food resource so that individual animals are dying one by one until there is enough food for the remaining animals, and if there are different variants of animals with different chances of finding food, then we can expect the animals that die to follow a Wallenius noncentral hypergeometric distribution. Fisher’s noncentral hypergeometric distribution may be used instead of Wallenius distribution in cases where the fates of the individual animals are independent and the total number of survivors is known or controlled as part of a simulation experiment (Fog 2008).

Wallenius distribution is a general model of biased sampling. Fisher’s noncentral hypergeometric distribution is used for statistical tests on contingency tables where the marginals are fixed (McCullagh and Nelder, 1983).

The multivariate Fishers and Wallenius noncentral hypergeometric distribution, are referred to the case where the type of different balls is greater than 2 and each ball has a different probability.

The two distributions are both equal to the (multivariate) hypergeometric distribution when the odds ratio is 1.

example

Wpdf =WNChygepdf(x, M, K, n, odds) Problem description.

example

Wpdf =WNChygepdf(x, M, K, n, odds, accuracy) Plot of the density.

Examples

expand all

Problem description.

we have 500 balls in the urn

M  = 500;
%initially, in the urn we have 250 red and 250 white balls
K  = M/2;
%we extract 3 balls, one at a time, without replacement
n  = 3;
%red balls have a probability ten times greater to be extracted thab white balls
odds  = 10;
% We compute the probability of getting 0, 1, 2 or 3 red balls in drawing
% 3 balls without replacement.
x = 0:n;
wpdf = WNChygepdf(x,M,K,n,odds);
disp('We have an urn with 2 groups of balls;');
disp('There are 250 balls in each group;');
disp('But the probability of getting a ball of one type is 10 times that of the other type;');
disp('The probability of getting 0, or 1, or 2, or 3 balls');
disp('of the first type in 3 (weighted) drawns is respectively:');
disp(wpdf);

We have an urn with 2 groups of balls;
There are 250 balls in each group;
But the probability of getting a ball of one type is 10 times that of the other type;
The probability of getting 0, or 1, or 2, or 3 balls
of the first type in 3 (weighted) drawns is respectively:
    0.0007    0.0225    0.2262    0.7505

Plot of the density.

we have M balls in the urn

M  = 200;
% We have K red balls
K  = 6;
%we extract n balls, one at a time, without replacement
n  = 5;
%red balls have a probability odds times greater to be extracted than white balls
odds  = 100;
% We compute the probability of getting 0, 1, 2 or 3, ..., n red balls 
x = 0:n;
wpdf = WNChygepdf(x,M,K,n,odds);
% Density
bar(x,wpdf)
xlabel('Number of successes')
ylabel('Point mass function')
title(['M=' num2str(M) ' K=' num2str(K)  ' n=' num2str(n) ' odds=' num2str(odds)])

Click here for the graphical output of this example (link to Ro.S.A. website).

Related Examples

expand all

Fisher Noncentral Hypergeometric Distributions Property 1.

Taken from Equation (12) of "Sampling Methods for Wallenius' and Fishers' Noncentral Hypergeometric Distributions" WNChygepdf(x,M,K,n,odds) should be equal to WNChygepdf(n-x,M,M-K,n,1/odds) up to some very small epsilon.

%
% we have 20 balls in the urn
M  = 20;
% initially, in the urn we have 250 red and 250 white balls
K  = M/2;
% we extract 3 balls without replacement
n  = 3;
% red balls have a probability ten times greater to be extracted thab white balls
odds  = 5;
% We compute the probability of getting 0, 1, 2 or 3 red balls in drawing
% 3 balls without replacement.
x = (0:n)';
Wpdfa = WNChygepdf(x,M,K,n,odds);
Wpdfb = WNChygepdf(n-x,M,M-K,n,1/odds);
assert(all(ismembertol(Wpdfa,Wpdfb,1E-12)), "Property 1 not verified.");