FSM
FSM computes forward search estimator in multivariate analysis
Description
Examples
 FSM with all default options.
FSM with all default options.
 FSM with all default options.
FSM with all default options.
n=200;
v=3;
randn('state', 123456);
Y=randn(n,v);
% Contaminated data
Ycont=Y; Ycont(1:5,[1,3]) = Ycont(1:5,[1,3])+sign(randn(5,2))*4.5;
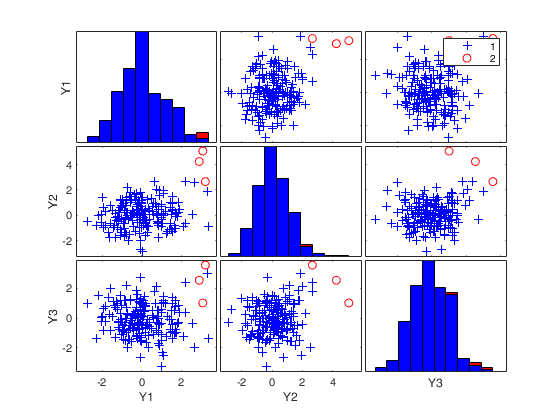
[out]=FSM(Ycont);
title('Outliers detected by FSM','Fontsize',24,'Interpreter','LaTex');
Warning: Using 'state' to set RANDN's internal state causes RAND, RANDI, and
RANDN to use legacy random number generators. This syntax is not recommended.
See <a href="matlab:helpview([docroot '\techdoc\math\math.map'],'update_random_number_generator')">Replace Discouraged Syntaxes of rand and randn</a> to use RNG to replace the
old syntax.
-------------------------
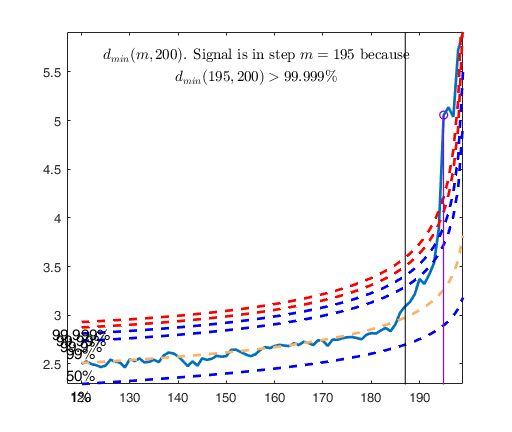
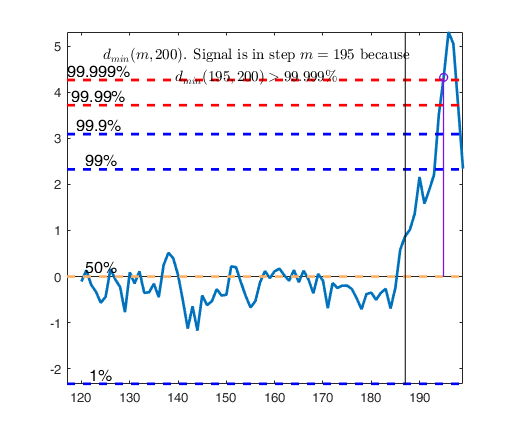
Signal detection loop
dmin(195,200)>99.9% and dmin(196,200)>99.9% and rmin(194,200)>99%
drmin(194,200)>99.9% and dmin(195,200)>99.9% and rmin(196,200)>99%
dmin(195,200)>99% at final step: Bonferroni signal in the final part of the search.
dmin(195,200)>99.999%
-------------------
Signal validation
Validated signal
-------------------------------
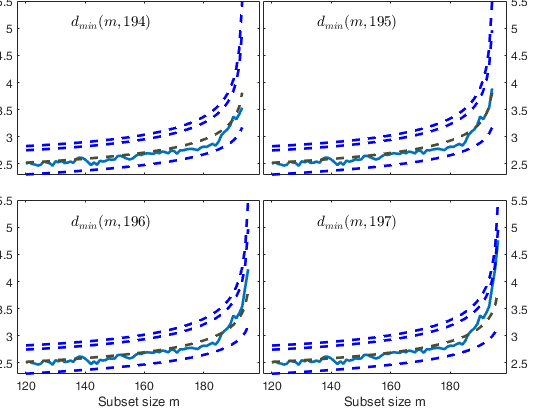
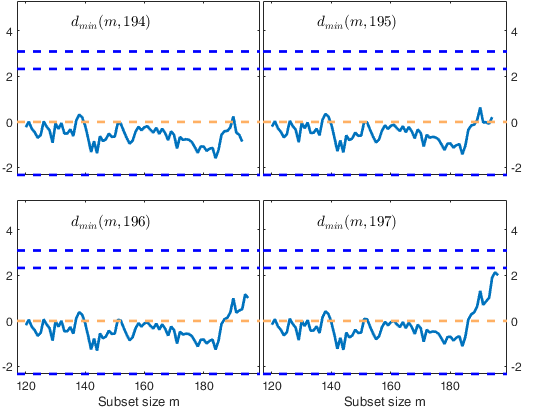
Start resuperimposing envelopes from step m=194
Superimposition stopped because d_{min}(195,196)>99% envelope
$d_{min}(195,196)>99$\% envelope
----------------------------
Final output
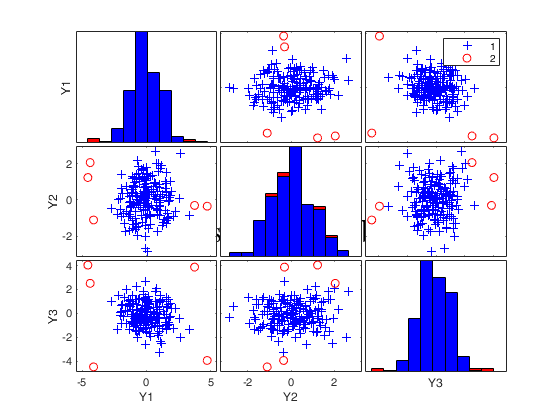
Number of units declared as outliers=5
Summary of the exceedances
1 99 999 9999 99999
0 6 6 4 4
 FSM with optional arguments.
FSM with optional arguments.
 FSM with optional arguments.
FSM with optional arguments.FSM with plots showing envelope superimposition.
n=200;
v=3;
randn('state', 123456);
Y=randn(n,v);
% Contaminated data
Ycont=Y;
Ycont(1:5,:)=Ycont(1:5,:)+3;
[out]=FSM(Ycont,'plots',2);
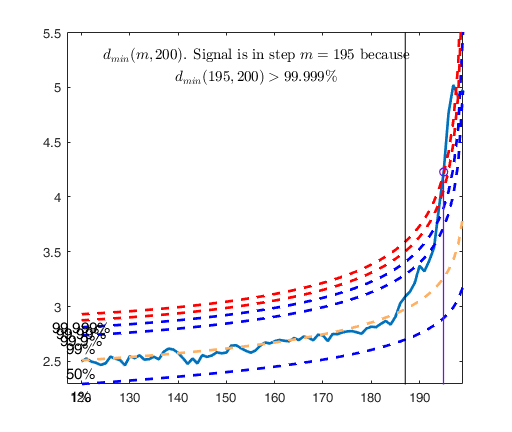
-------------------------
Signal detection loop
dmin(195,200)>99.9% and dmin(196,200)>99.9% and rmin(194,200)>99%
drmin(194,200)>99.9% and dmin(195,200)>99.9% and rmin(196,200)>99%
dmin(195,200)>99.999%
-------------------
Signal validation
Validated signal
-------------------------------
Start resuperimposing envelopes from step m=194
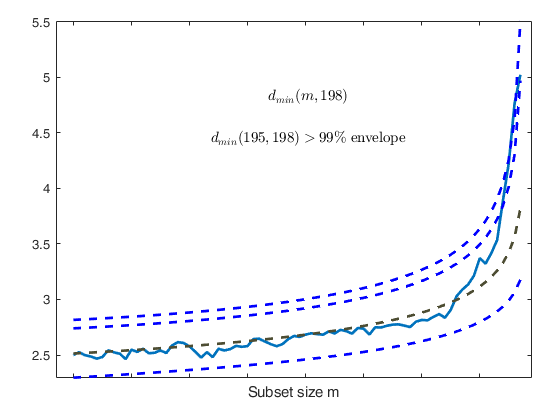
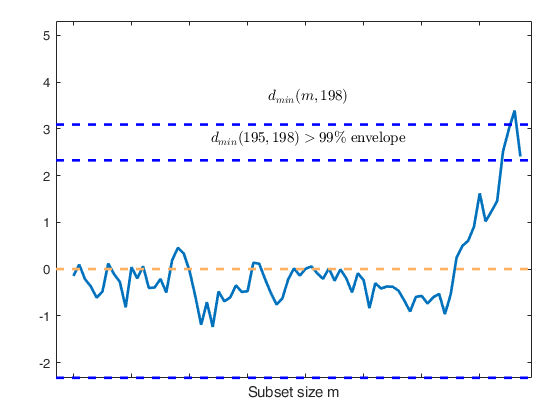
Superimposition stopped because d_{min}(195,198)>99% envelope
$d_{min}(195,198)>99$\% envelope
Subsample of 197 units is homogeneous
----------------------------
Final output
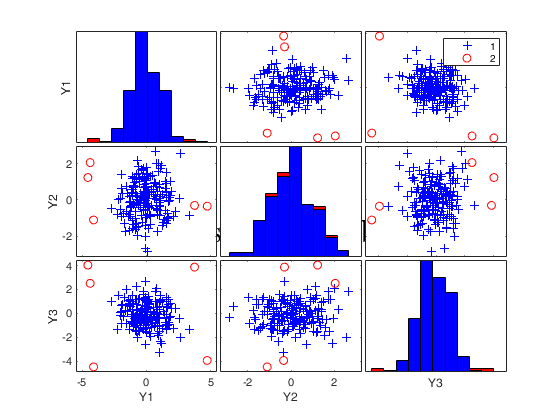
Number of units declared as outliers=3
Summary of the exceedances
1 99 999 9999 99999
0 6 5 3 3
Related Examples
 FSM with plots showing envelope superimposition in normal
coordinates.
FSM with plots showing envelope superimposition in normal
coordinates.
 FSM with plots showing envelope superimposition in normal
coordinates.
FSM with plots showing envelope superimposition in normal
coordinates.
n=200;
v=3;
randn('state', 123456);
Y=randn(n,v);
% Contaminated data
Ycont=Y;
Ycont(1:5,:)=Ycont(1:5,:)+3;
plots=struct;
plots.ncoord=1;
[out]=FSM(Ycont,'plots',plots);
-------------------------
Signal detection loop
dmin(195,200)>99.9% and dmin(196,200)>99.9% and rmin(194,200)>99%
drmin(194,200)>99.9% and dmin(195,200)>99.9% and rmin(196,200)>99%
dmin(195,200)>99.999%
-------------------
Signal validation
Validated signal
-------------------------------
Start resuperimposing envelopes from step m=194
Superimposition stopped because d_{min}(195,198)>99% envelope
$d_{min}(195,198)>99$\% envelope
Subsample of 197 units is homogeneous
----------------------------
Final output
Number of units declared as outliers=3
Summary of the exceedances
1 99 999 9999 99999
0 6 5 3 3
Monitor the exceedances from m=200 without showing plots.
n=1000;
v=10;
Y=randn(n,v);
[out]=FSM(Y,'init',200,'plots',0);
Choosing an initial subset formed by the three observations with
the smallest Mahalanobis Distance.
n=100;
v=3;
Y=randn(n,v);
% Contaminated data
Ycont=Y;
Ycont(1:5,:)=Ycont(1:5,:)+3;
[out]=FSM(Ycont,'m0',5,'crit','md');
Forgery Swiss banknotes examples.
load('swiss_banknotes');
Y=swiss_banknotes{:,:};
% Monitor the exceedances of Minimum Mahalanobis Distance
[out]=FSM(Y(101:200,:),'plots',1);
% Control minimum and maximum on the x axis
plots=struct;
plots.xlim=[60 90];
[out]=FSM(Y(101:200,:),'plots',plots);
% Monitor the exceedances of Minimum Mahalanobis Distance using normal coordinates for mmd.
plots.ncoord=1;
[out]=FSM(Y(101:200,:),'plots',plots);
Input Arguments
Y — Input data.
Matrix.
n x v data matrix; n observations and v variables. Rows of Y represent observations, and columns represent variables.
Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.
Data Types: single|double
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'bonflev',0.7
, 'crit','md'
, 'init',50
, 'm0',5
, 'msg',0
, 'nocheck',1
, 'rf',0.9
, 'plots',2
bonflev
—option that might be used to identify extreme outliers
when the distribution of the data is strongly non normal.scalar.
In these circumstances, the general signal detection rule based on consecutive exceedances cannot be used. In this case bonflev can be: - a scalar smaller than 1, which specifies the confidence level for a signal and a stopping rule based on the comparison of the minimum deletion residual with a Bonferroni bound. For example if bonflev=0.99 the procedure stops when the trajectory exceeds for the first time the 99% bonferroni bound.
- A scalar value greater than 1. In this case the procedure stops when the residual trajectory exceeds for the first time this value.
Default value is ' ', which means to rely on general rules based on consecutive exceedances.
Example: 'bonflev',0.7
Data Types: double
crit
—It specified the criterion to be used to
initialize the search.'md' (default) | 'biv' | 'uni.
if crit='md' (default) the units which form initial subset are those which have the smallest m0 Mahalanobis distances (defined as sum of bivariate robust Mahalanobis distances) computed using procedure unibiv (bivariate robust ellipses).
if crit='biv' sorting is done first in terms of times units fell outside robust bivariate ellipses and then in terms of Mahalanobis distances. In other words, the units forming initial subset are chosen first among the set of those which never fell outside robust bivariate ellipses then among those which fell only once outside bivariate ellipses ... up to reach m0.
if crit='uni' sorting is done first in terms of number of times units fell outside univariate boxplots and then in terms of Mahalanobis distances. In other words, the units forming initial subset are chosen first among the set of those which never fell outside univariate boxplots then among those which fell only once outside univariate boxplots... up to reach m0.
Remark: as the user can see the starting point of the search is not going to affect at all the results of the analysis. The user can explore this point with his own datasets.
Remark: if crit='biv' the user can also supply in scalar rf (see below) the confidence level of the bivariate ellipses.
Example: 'crit','md'
Data Types: char
init
—Point where to start monitoring required diagnostics.scalar.
Note that if initial subset is supplied (that is input option m0 is a vector of length greater than 1) init must be greater or equal than length(m0). If init is not specified it will be set equal to floor(n*0.6).
Example: 'init',50
Data Types: double
m0
—Initial subset size or vector which contains the list of
the units forming initial subset.scalar | vector.
The default is , that is we start the search with v+1 units.
The v+1 units are chosen according to input option 'crit'.
If on the other hand, m0 is a vector of length greater than 1 it contains the indexes of the units which must form the initial susbet. For example if m0=[1;3;10;23;45];
the initial subset is formed by units 1, 3, 10, 23 and 45. Note that if m0 is a vector of length greater than 1, option crit is ignored.
Example: 'm0',5
Data Types: double
msg
—It controls whether to display or not messages
on the screen.boolean.
If msg==1 (default) messages about the progression of the search are displayed on the screen otherwise only error messages will be displayed.
Example: 'msg',0
Data Types: logical
nocheck
—It controls whether to perform checks on matrix Y.scalar.
If nocheck is equal to 1 no check is performed.
As default nocheck=0.
Example: 'nocheck',1
Data Types: double
rf
—confidence level for bivariate ellipses.scalar.
The default is 0.95. This option is used only if crit='biv' and input option m0 is not a vector with length greater than 1.
Example: 'rf',0.9
Data Types: double
plots
—plot of minimum Mahalanobis distance.scalar | structure.
If plots is a missing value or is a scalar equal to 0 no plot is produced.
If plots is a scalar equal to 1 (default) the plot of minimum MD with envelopes based on n observations and the scatterplot matrix with the outliers highlighted is produced.
If plots is a scalar equal to 2 the additional plots of envelope resuperimposition are produced.
If plots is a structure it may contain the following fields:
| Value | Description |
|---|---|
ylim |
vector with two elements controlling minimum and maximum on the y axis. Default value is '' (automatic scale); |
xlim |
vector with two elements controlling minimum and maximum on the x axis. Default value is '' (automatic scale); |
resuper |
vector which specifies for which steps it is necessary to show the plots of resuperimposed envelopes if resuper is not supplied a plot of each step in which the envelope is resuperimposed is shown. Example if resuper =[85 87] plots of resuperimposedenvelopes are shown at steps m=85 and m=87; |
ncoord |
boolean. If ncoord=true plots are shown in normal coordinates else (default) plots are shown in traditional mmd coordinates; |
labeladd |
If this option is '1', the outliers in the spm are labelled with the unit row index. The default value is labeladd='', i.e. no label is added; |
nameY |
cell array of strings containing the labels of the variables. As default value, the labels which are added are Y1, ...Yv; |
lwd |
Scalar which controls line width of the curve which contains the monitoring of minimum Mahalanobis distance. Default line of lwd=2. |
lwdenv |
Scalar which controls linewidth of the envelopes. Default value of lwdenv=2. |
Example: 'plots',2
Data Types: double
Output Arguments
out — description
Structure
Structure which contains the following fields
| Value | Description |
|---|---|
outliers |
k x 1 vector containing the list of the units declared as outliers or empty value if the sample is homogeneous |
mmd |
(n-init) x 2 matrix. 1st col = fwd search index; 2nd col = value of minimum Mahalanobis Distance in each step of the fwd search. |
Un |
(n-init) x 11 Matrix which contains the unit(s) included in the subset at each step of the fwd search. REMARK: in every step the new subset is compared with the old subset. Un contains the unit(s) present in the new subset but not in the old one. Un(1,2) for example contains the unit included in step init+1. Un(end,2) contains the units included in the final step of the search. |
nout |
2 x 5 matrix containing the number of times mmd went out of particular quantiles. First row contains quantiles 1 99 99.9 99.99 99.999 per cent; Second row contains the frequency distribution. It is NaN if bonflev threshold is used. |
loc |
1 x v vector containing location of the data. |
cov |
v x v robust estimate of covariance matrix. |
md |
n x 1 vector containing the estimates of the robust Mahalanobis distances (in squared units). This vector contains the distances of each observation from the location of the data, relative to the scatter matrix cov. |
class |
'FSM'. |
References
Riani, M., Atkinson, A.C. and Cerioli, A. (2009), Finding an unknown number of multivariate outliers, "Journal of the Royal Statistical Society Series B", Vol. 71, pp. 201-221.
Cerioli, A., Farcomeni, A. and Riani M. (2014), Strong consistency and robustness of the Forward Search estimator of multivariate location and scatter, "Journal of Multivariate Analysis", Vol. 126, pp. 167-183, http://dx.doi.org/10.1016/j.jmva.2013.12.010