FSMeda

FSMeda performs forward search in multivariate analysis with exploratory data analysis purposes

expand all in page

Syntax

Description

example

out =FSMeda(Y, bsb) FSMeda with all default options.

example

out =FSMeda(Y, bsb, Name, Value) FSMeda with optional arguments.

Examples

expand all

  • FSMeda with all default options.

    • Run the FS on a simulated dataset by choosing an initial subset formed by the three observations with the smallest Mahalanobis Distance. 

    n=100;
v=3;
m0=4;
Y=randn(n,v);
% Contaminated data
Ycont=Y;
Ycont(1:5,:)=Ycont(1:5,:)+3;
[fre]=unibiv(Y);
%create an initial subset with the 3 observations with the lowest
%Mahalanobis Distance
fre=sortrows(fre,4);
bs=fre(1:m0,1);
[out]=FSMeda(Ycont,bs);

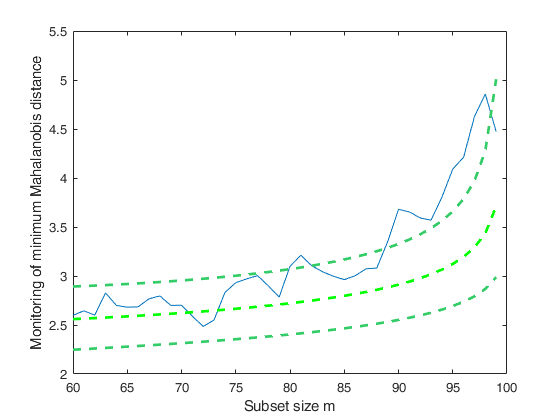
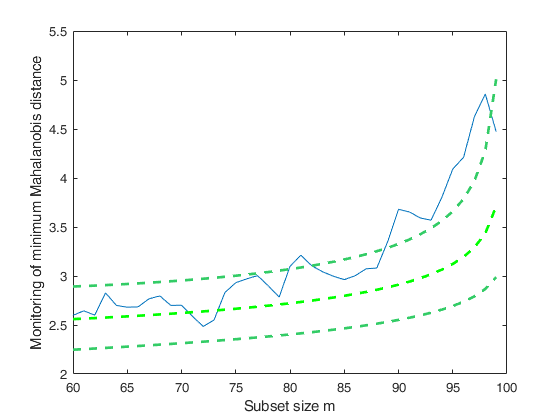
  • FSMeda with optional arguments.

    • Monitoring the evolution of minimum Mahalanobis distance. 

    n=100;
v=3;
m0=3;
Y=randn(n,v);
% Contaminated data
Ycont=Y;
Ycont(1:5,:)=Ycont(1:5,:)+3;
[fre]=unibiv(Y);
%create an initial subset with the 3 observations with the lowest
%Mahalanobis Distance
fre=sortrows(fre,4);
bs=fre(1:m0,1);
[out]=FSMeda(Ycont,bs,'plots',1);
    Warning: Matrix is close to singular or badly scaled. Results may be
inaccurate. RCOND =  2.781704e-18. 
Warning: Matrix is close to singular or badly scaled. Results may be
inaccurate. RCOND =  4.471732e-19.
    Click here for the graphical output of this example (link to Ro.S.A. website).

    Related Examples

    expand all

  • Example with the Swiss bank notes data.

    • load('swiss_banknotes');
Y=swiss_banknotes{:,:};
[fre]=unibiv(Y);
%create an initial subset with the 3 observations with the lowest
%Mahalanobis Distance
fre=sortrows(fre,4);
m0=20;
bs=fre(1:m0,1);
[out]=FSMeda(Y,bs,'plots',1,'init',30);
    Click here for the graphical output of this example (link to Ro.S.A. website)

  • Example with the Emilia Romagna data.

    • load('emilia2001')
Y=emilia2001{:,:};
[fre]=unibiv(Y);
%create an initial subset with the 30 observations with the lowest
%Mahalanobis Distance
fre=sortrows(fre,4);
m0=30;
bs=fre(1:m0,1);
[out]=FSMeda(Y,bs,'init',100);
% Minimum Mahalanobis distance
% Compare the plot with Figure 1.12 p. 21, ARC (2004)
mmdplot(out,'ylimy',[6 14])
% Analysis of the last 16 units to enter the forward search
% Compare the results with Table 1.3 p. 21
disp(out.Un(end-15:end,:));

  • Example with the Emilia Romagna data (all variables).

    • load('emilia2001')
Y=emilia2001{:,:};
% Replace zeros with min values for variables specified in sel
sel=[6 10 12 13 19 21];
for i=sel
Y(Y(:,i)==0,i)=min(Y(Y(:,i)>0,i));
end
% Modify variables y16 y23 y25 y26
sel=[16 23 25 26];
sel=[25 26];
Y1=Y;
Y1(:,sel)=100-Y1(:,sel);
la0demo=[0.5,0.25,0,1,0.25,0,0,0.25,0.5];
la0weal=[0.25,0.5,0.5,1,1,0.5,-1/3,0.25,0.25,-1];
la0work=[0.25,0,1,0,0,0.25,1,1,1];
la0C2=[la0demo(1:5) la0work(1:4) la0demo(6:9) la0weal la0work(5:9)];
Y1tr=normBoxCox(Y1,1:28,la0C2);
[fre]=unibiv(Y1tr);
%create an initial subset with the 30 observations with the lowest
%Mahalanobis Distance
fre=sortrows(fre,4);
m0=30;
bs=fre(1:m0,1);
[out]=FSMeda(Y1tr,bs,'init',100,'scaled',1);
% Minimum Mahalanobis distance
[out]=FSMeda(Y1tr,bs,'init',100);
mmdplot(out,'ylimy',[5 26])
standard=struct;
standard.ylim=[4 17];
malfwdplot(out,'standard',standard);

    Input Arguments

    expand all

    Y — Input data. Matrix.

    n x v data matrix; n observations and v variables. Rows of Y represent observations, and columns represent variables. Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.

    Data Types: single | double

    bsb — Units forming subset. Vector.

    List of units forming the initial subset.

    If bsb=0 (default) then the procedure starts with v units randomly chosen else if bsb is not 0 the search will start with m0=length(bsb).

    Data Types: single | double

    Name-Value Pair Arguments

    Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

    Example: 'init',50 , 'plots',0 , 'msg',0 , 'scaled',0 , 'nocheck',1

    init —Point where to start monitoring required diagnostics.scalar.

    Note that if bsb is supplied, init>=length(bsb). If init is not specified it will be set equal to floor(n*0.6).

    Example: 'init',50

    Data Types: double

    plots —It specify whether it is necessary to produce the plots of the monitoring of minMD.scalar.

    If plots=1, a plot of the monitoring of minMD among the units not belonging to the subset is produced on the screen with 1 per cent, 50 per cent and 99 per cent confidence bands else (default), all plots are suppressed.

    Example: 'plots',0

    Data Types: double

    msg —It controls whether to display or not messages about great interchange on the screen.scalar.

    If msg==1 (default) messages are displyed on the screen else no message is displayed on the screen.

    Example: 'msg',0

    Data Types: double

    scaled —It controls whether to monitor scaled Mahalanobis distances.scalar.

    If scaled=1 Mahalanobis distances monitored during the search are scaled using ratio of determinant.

    If scaled=2 Mahalanobis distances monitored during the search are scaled using asymptotic consistency factor.

    The default value is 0 that is Mahalanobis distances are not scaled.

    Example: 'scaled',0

    Data Types: double

    nocheck —It controls whether to perform checks on matrix Y.scalar.

    If nocheck is equal to 1 no check is performed on matrix Y. As default nocheck=0.

    Example: 'nocheck',1

    Data Types: double

    Output Arguments

    expand all

    out — description Structure

    Structure which contains the following fields

    Value Description
    MAL

    n x (n-init+1) = matrix containing the monitoring of Mahalanobis distances.

    1st row = distance for first unit;

    ...;

    nth row = distance for nth unit.
    BB

    n x (n-init+1) matrix containing the information about the units belonging to the subset at each step of the forward search.

    1st col = indexes of the units forming subset in the initial step;

    ...;

    last column = units forming subset in the final step (all units).
    mmd

    n-init x 3 matrix which contains the monitoring of minimum MD or (m+1)th ordered MD at each step of the forward search.

    1st col = fwd search index (from init to n-1);

    2nd col = minimum MD;

    3rd col = (m+1)th-ordered MD.
    msr

    n-init+1 x 3 = matrix which contains the monitoring of maximum MD or mth ordered MD.

    1st col = fwd search index (from init to n);

    2nd col = maximum MD;

    3rd col = mth-ordered MD.
    gap

    n-init+1 x 3 = matrix which contains the monitoring of the gap (difference between minMD outside subset and max.

    inside).

    1st col = fwd search index (from init to n);

    2nd col = min MD - max MD;

    3rd col = (m+1)th ordered MD - mth ordered distance.
    Loc

    (n-init+1) x (v+1) matrix containing the monitoring of estimated of the means for each variable in each step of the forward search.
    S2cov

    (n-init+1) x (v*(v+1)/2+1) matrix containing the monitoring of the elements of the covariance matrix in each step of the forward search.

    1st col = fwd search index (from init to n);

    2nd col = monitoring of S(1,1);

    3rd col = monitoring of S(1,2);

    ...;

    end col = monitoring of S(v,v).
    detS

    (n-init+1) x (2) matrix containing the monitoring of the determinant of the covariance matrix in each step of the forward search.
    Un

    (n-init) x 11 Matrix which contains the unit(s) included in the subset at each step of the fwd search.

    REMARK: in every step the new subset is compared with the old subset. Un contains the unit(s) present in the new subset but not in the old one Un(1,2) for example contains the unit included in step init+1 Un(end,2) contains the units included in the final step of the search
    Y

    Original data input matrix
    class

    'FSMeda'

    References

    Atkinson, A.C., Riani, M. and Cerioli, A. (2004), "Exploring multivariate data with the forward search", Springer Verlag, New York.

    See Also

    |

    This page has been automatically generated by our routine publishFS