Vector containing strictly numerical data.
Note that if x is referred to a continuous variable x(1)
represent the lower extreme of the first class, and the other
values of x contain the upper extremes of the other
classes.
Data Types: double, ordered categorical
Requested probabilities for which to compute the quantile,
specified as a scalar.
Data Types: double
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
Example:
'freq',1:10
, 'DiscreteData',false
, 'plots',true
Vector of the same length of x containing the frequencies
(weights) associated to each value of x if x is discrete or
vector with length (x)-1 if variable X is continuous. If
freq is not supplied, it is assumed that all observations have the
same (relative) frequency (weight).
Example: 'freq',1:10
Data Types: double
If DiscreteData is true (default), we assume that the data
in x come from a discrete variable.
If DiscreteData is false, we assume that the data
in x come from a continuous variable.
Example: 'DiscreteData',false
Data Types: boolean
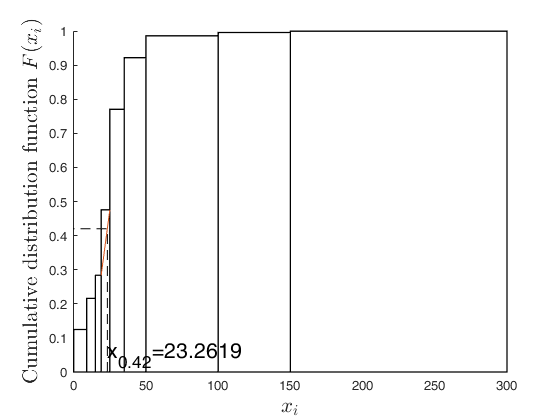
If plots is true an additional plot which shows
graphically how the quantile has been obtained using the
linear interpolation is displayed on the screen. The
default value of plots is false.
Example: 'plots',true
Data Types: boolean
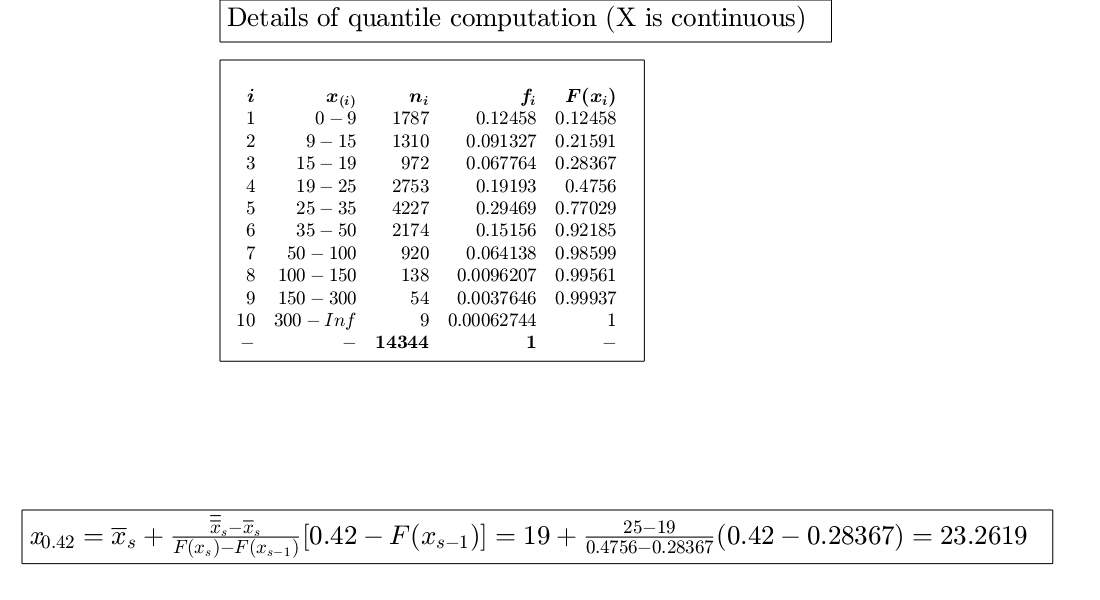
 Example of computation of 40 per cent percentile in a frequency
distribution (X is continuous).
Example of computation of 40 per cent percentile in a frequency
distribution (X is continuous).