GUIregress
GUIregress shows the necessary calculations to obtain simple linear regression statistics in a GUI.
Description
Examples
 Calculation of unweighted regression.
Calculation of unweighted regression.
 Calculation of unweighted regression.
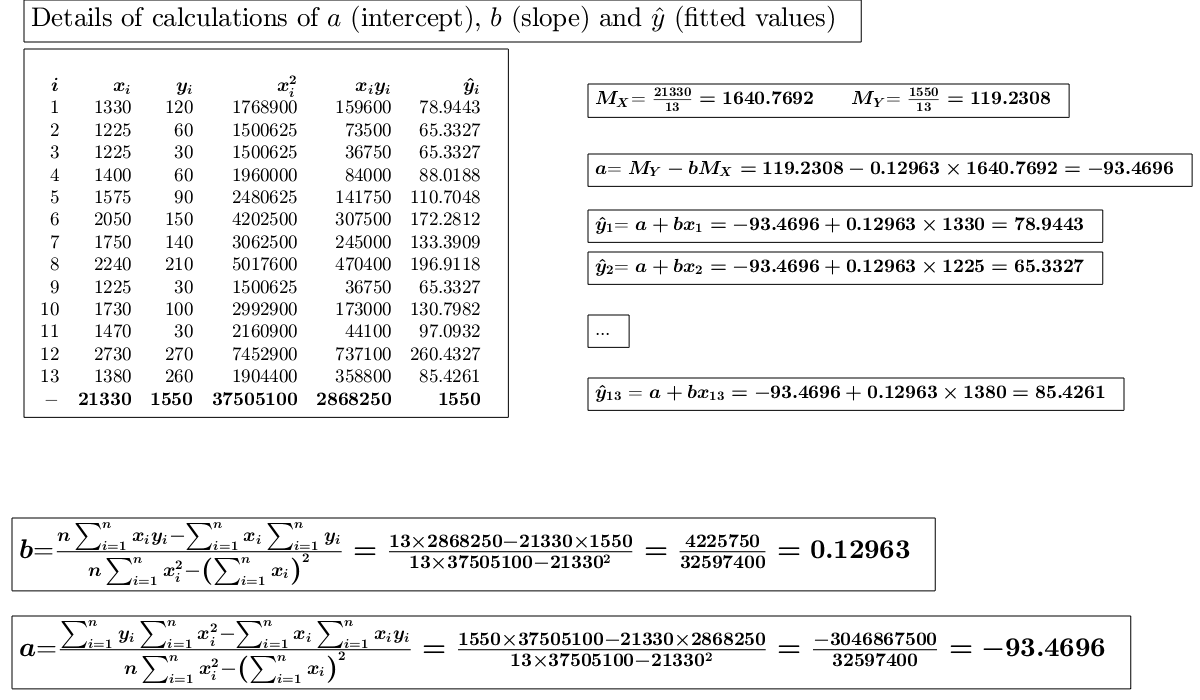
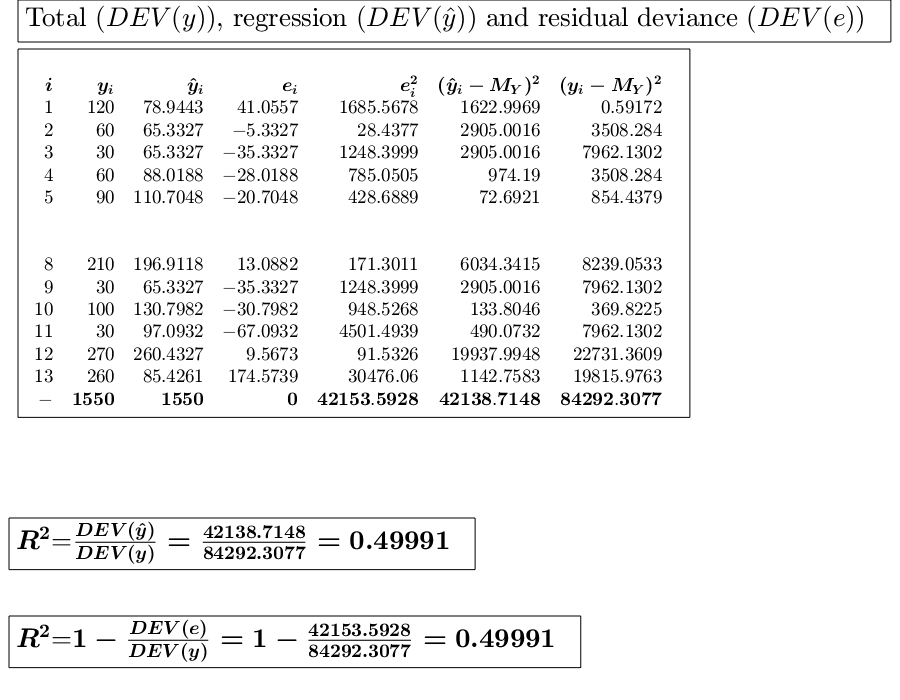
Calculation of unweighted regression.In this example we know the monthly income of 13 families and we estimate the correlation with the free time expenditure. (See page 223 of [MRZ]).
% x= monthly income of 13 families. % y= free time expenditure. x=[1330 1225 1225 1400 1575 2050 1750 2240 1225 1730 1470 2730 1380]; y=[120 60 30 60 90 150 140 210 30 100 30 270 260]; out=GUIregress(x,y);
 Use of option plots.
Use of option plots.
 Use of option plots.
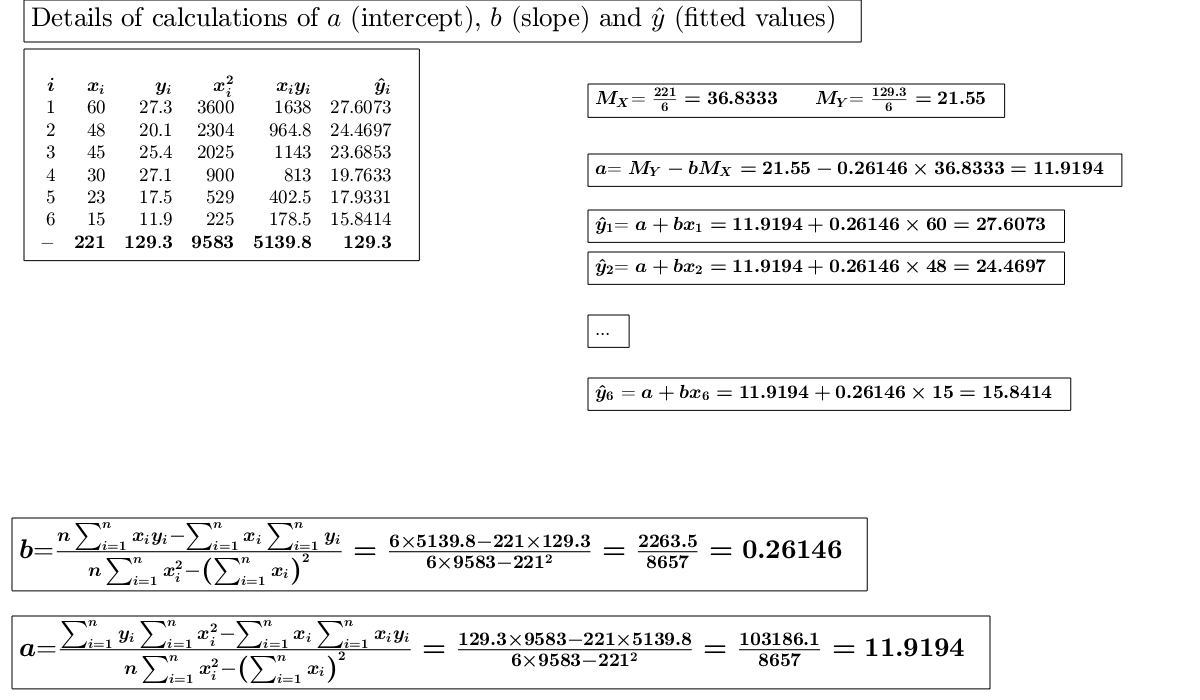
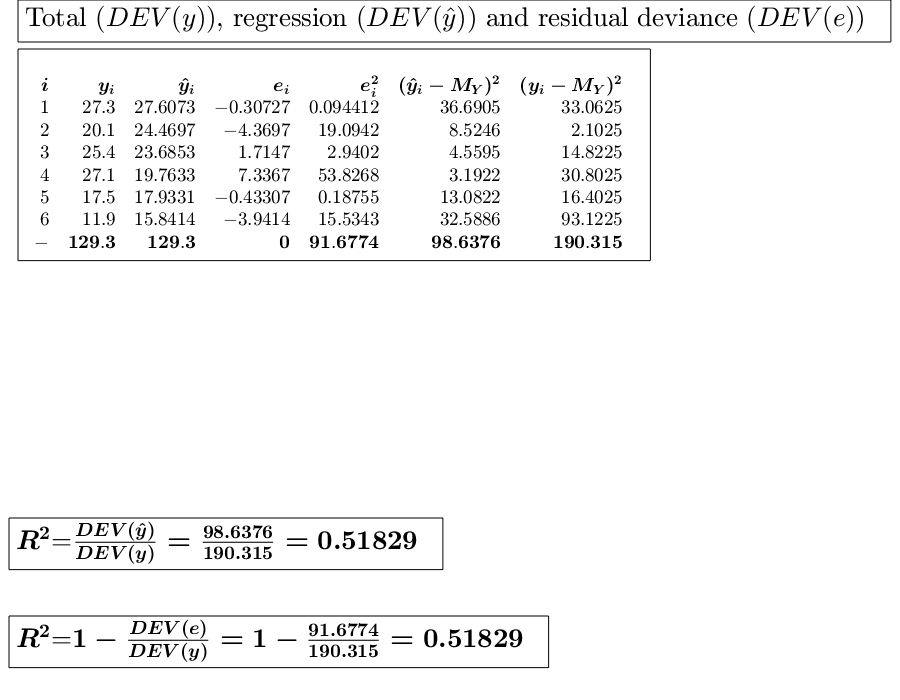
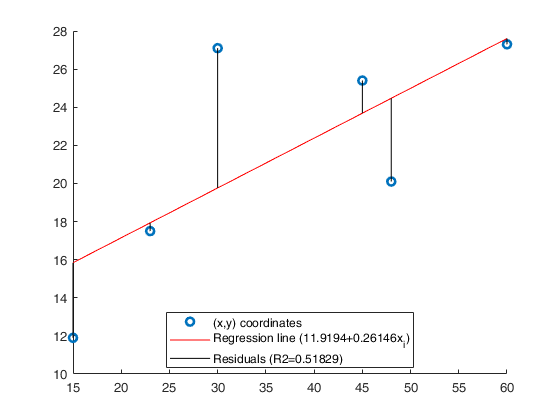
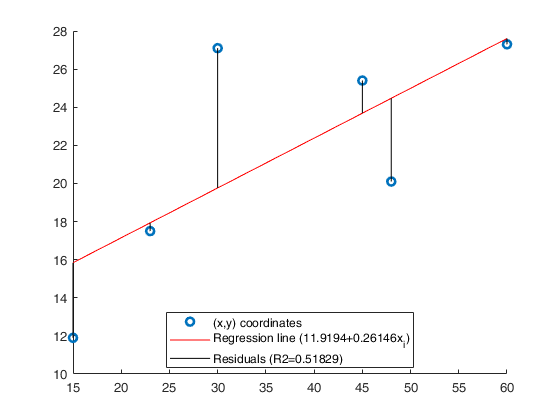
Use of option plots.The following data matrix reports, for 6 countries, the tourism revenues (y) recorded in a given year (in billions of dollars) and the number of foreign visitors (x) in the same year (in millions of units). (See page 101 of [CMR])
x=[60 48 45 30 23 15]; y=[27.3 20.1 25.4 27.1 17.5 11.9]; out=GUIregress(x,y,'plots',true);
ans =
Legend ((x,y) coordinates, Regression line (11.9194+0.26146x…) with properties:
String: {1×3 cell}
Location: 'best'
Orientation: 'vertical'
FontSize: 9.00
Position: [0.73 0.21 0.17 0.07]
Units: 'normalized'
Use GET to show all properties

Related Examples
 Use of option intercept.
Use of option intercept.
 Use of option intercept.
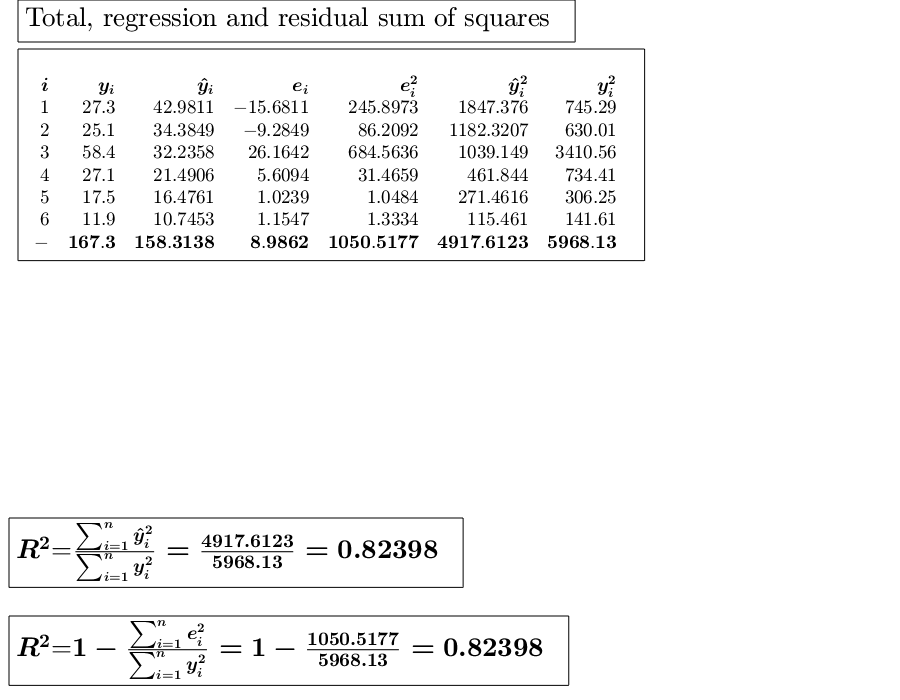
Use of option intercept.The following data matrix reports, for 6 countries, the tourism revenues (y) recorded in a given year (in billions of dollars) and the number of foreign visitors (x) in the same year (in millions of units). (See page 101 of [CMR])
x=[60 48 45 30 23 15]; y=[27.3 25.1 58.4 27.1 17.5 11.9]; out=GUIregress(x,y,'intercept',false,'plots',false);
First argument passed as table.
The following data matrix reports, for 6 countries, the tourism revenues (y) recorded in a given year (in billions of dollars) and the number of foreign visitors (x) in the same year (in millions of units). (See page 101 of [CMR])
x=[60 48 45 30 23 15];
y=[27.3 25.1 58.4 27.1 17.5 11.9];
XX=array2table([x' y'],'VariableNames',{'x','y'});
out=GUIregress(XX);
 Example of exponential interpolation.
Example of exponential interpolation.
 Example of exponential interpolation.
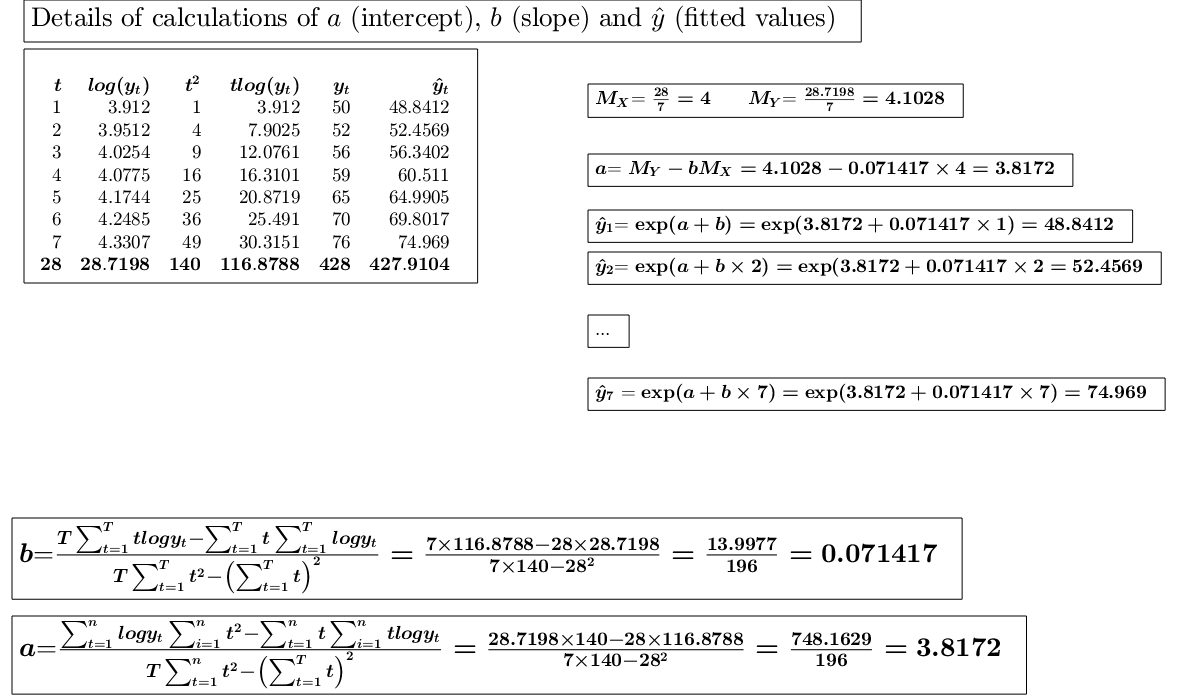
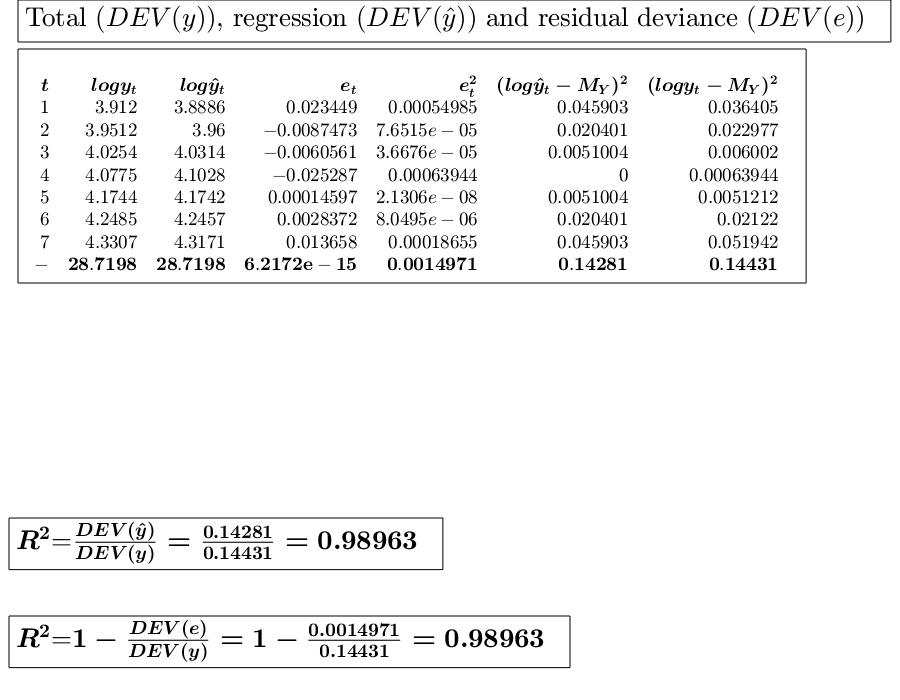
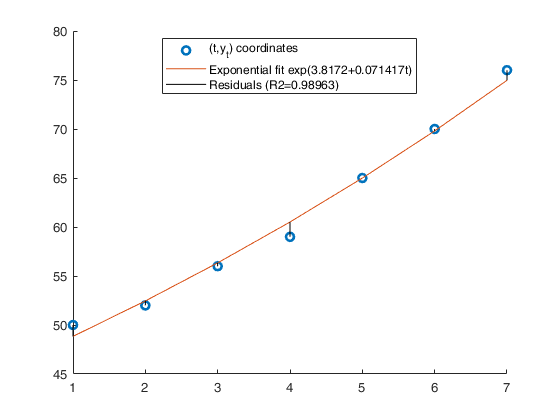
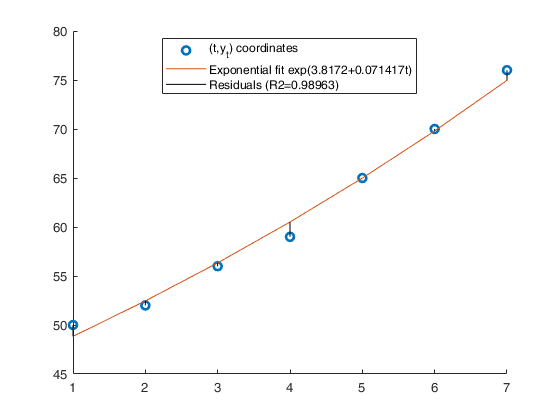
Example of exponential interpolation.The values of a company's production, in millions of euros were as follows: (See page 116 of [CMR])
x=1:7; y=[50 52 56 59 65 70 76]; % Analyze the trend of the company's production using an exponential fit. out=GUIregress([],y,'interpolant','exponential','plots',true,'timeseries', true);
ans =
Legend ((t,y_t) coordinates, Exponential fit exp(3.8172+0.07…) with properties:
String: {1×3 cell}
Location: 'best'
Orientation: 'vertical'
FontSize: 9.00
Position: [0.14 0.85 0.17 0.07]
Units: 'normalized'
Use GET to show all properties
 Example of power interpolation.
Example of power interpolation.
 Example of power interpolation.
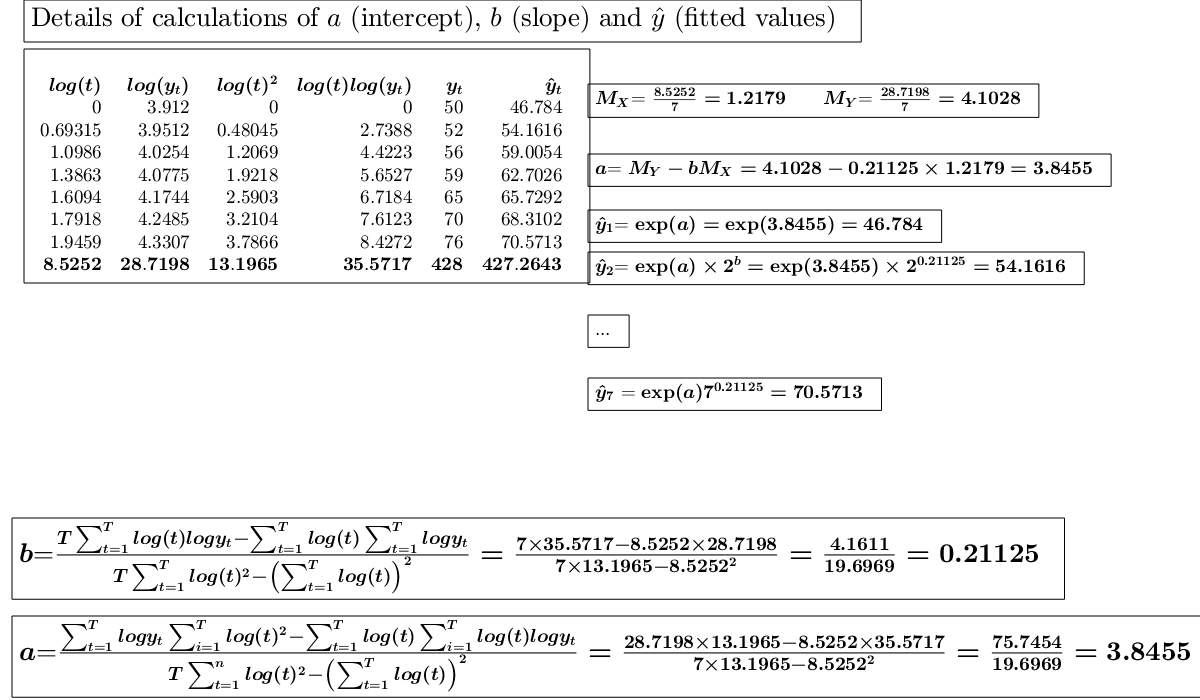
Example of power interpolation.The values of a company's production, in millions of euros were as follows: (See page 116 of [CMR])
x=1:7; y=[50 52 56 59 65 70 76]; % Analyze the trend of the company's production using a power fit. out=GUIregress(x,y,'interpolant','power','plots',true,'timeseries', true);
ans =
Legend ((t,y_t) coordinates, Power fit 46.784t^{0.21125}, Re…) with properties:
String: {1×3 cell}
Location: 'best'
Orientation: 'vertical'
FontSize: 9.00
Position: [0.77 0.13 0.12 0.07]
Units: 'normalized'
Use GET to show all properties
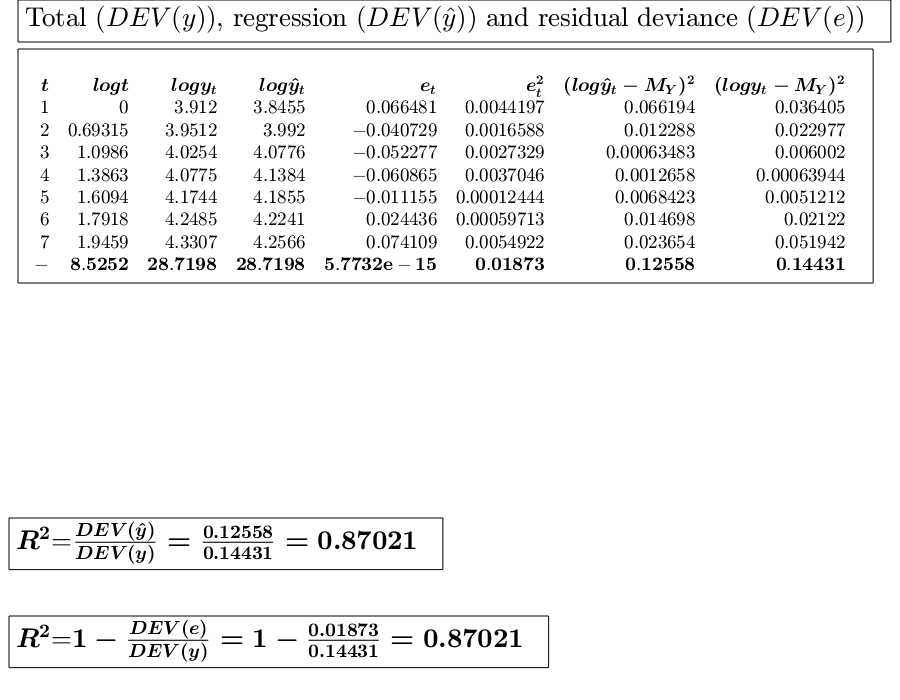
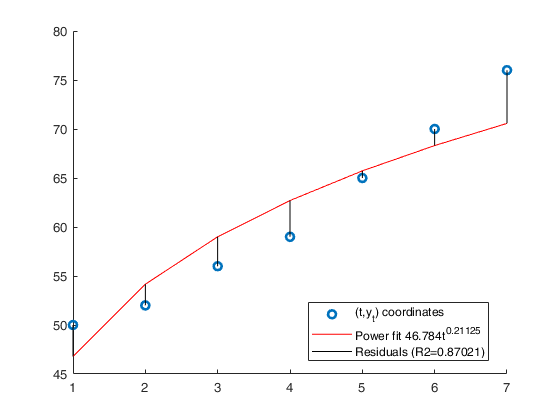
 Example of linear, exponential and power interpolation.
Example of linear, exponential and power interpolation.
 Example of linear, exponential and power interpolation.
Example of linear, exponential and power interpolation.Time series of the value of a commodity, in euros were as follows: (See page 269 of [MRZ])
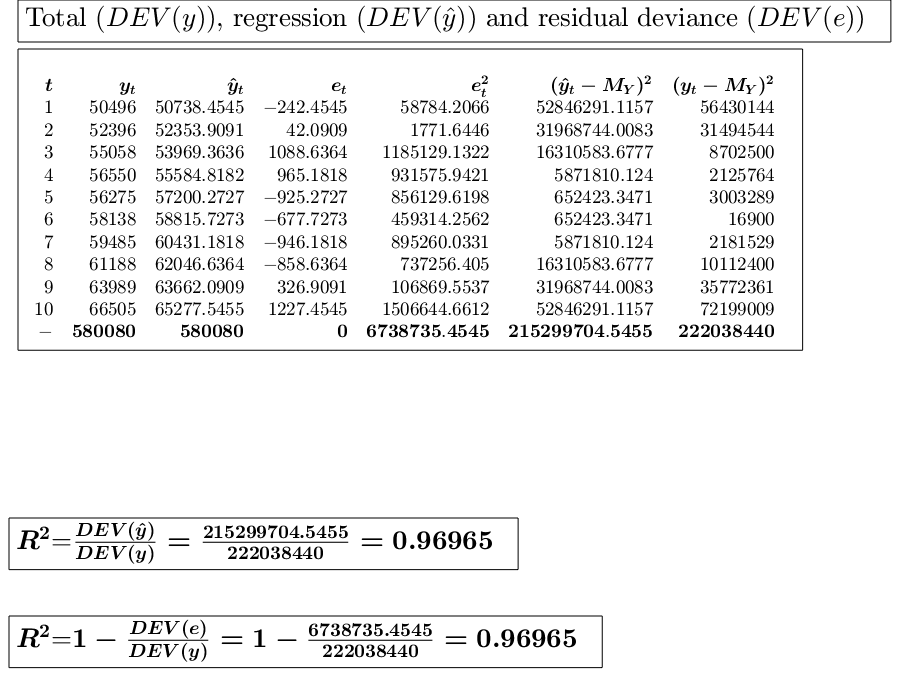
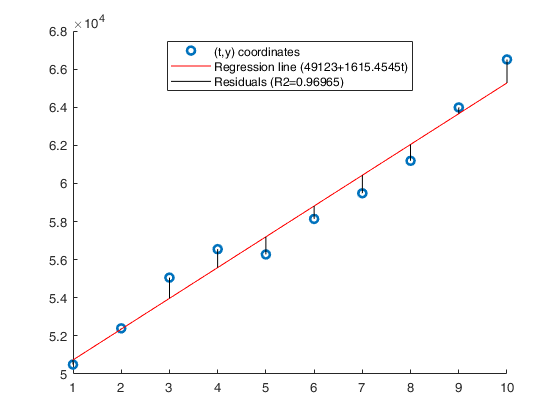
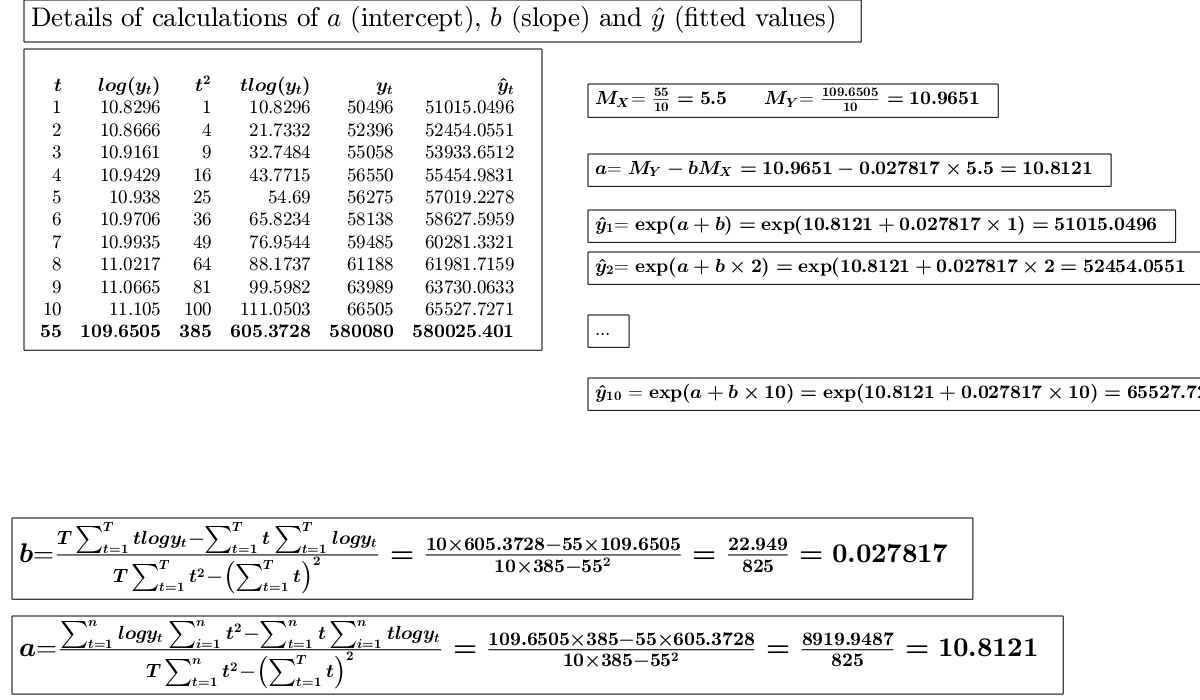
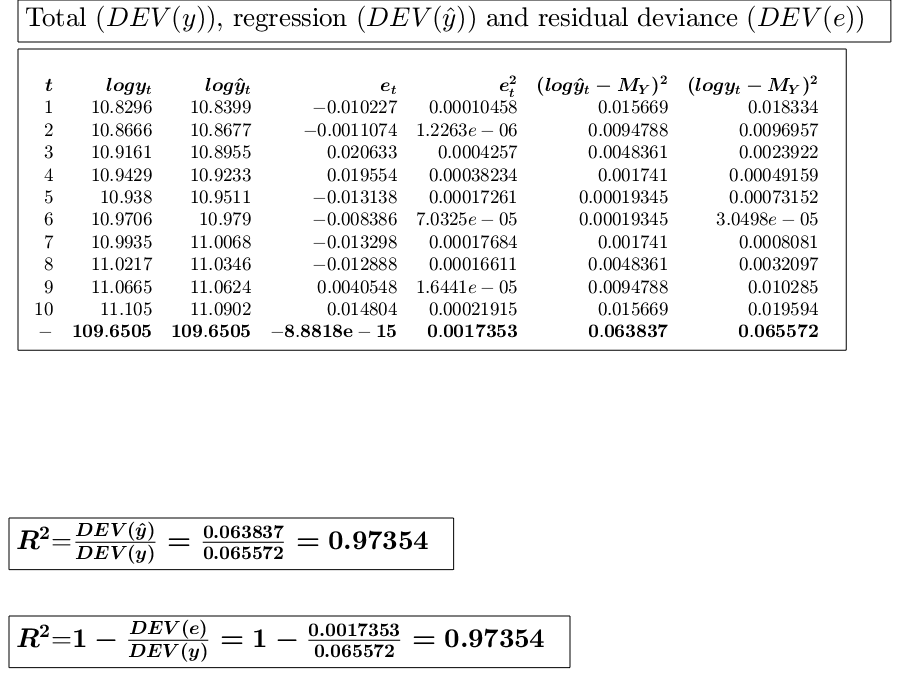
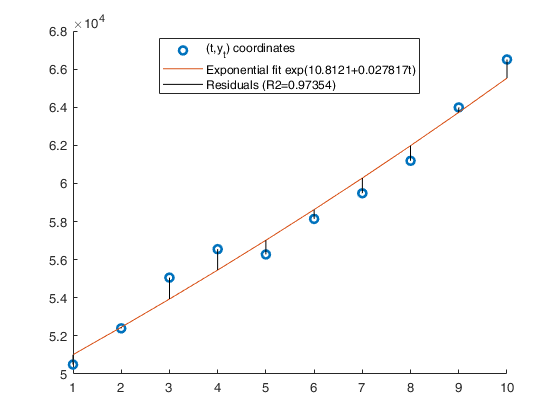
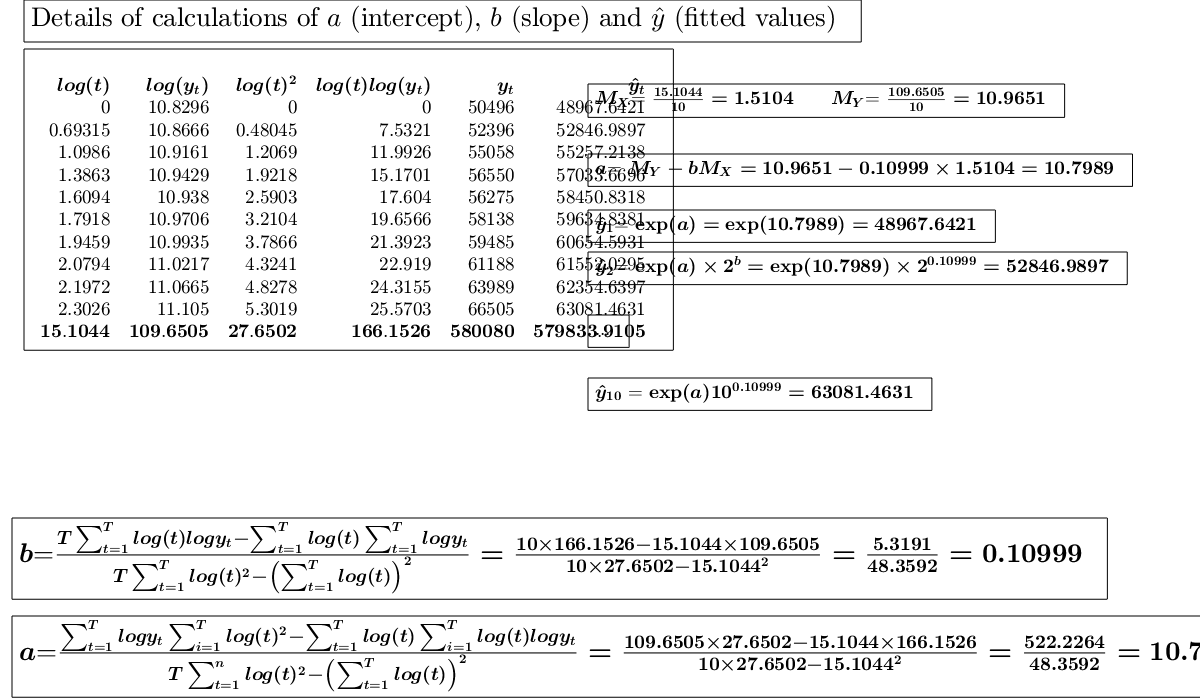
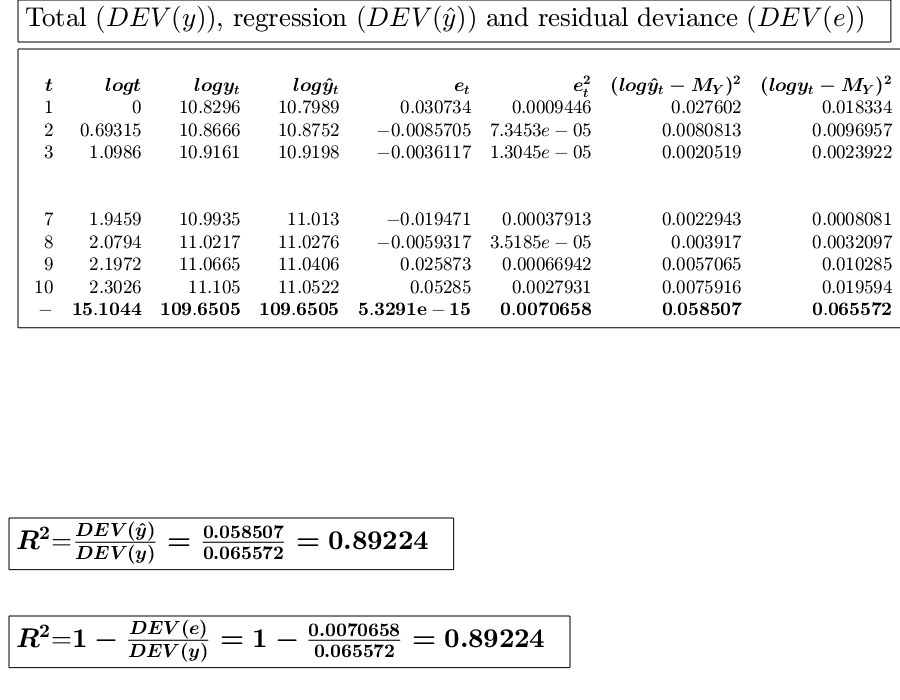
y=[50496 52396 55058 56550 56275 58138 59485 61188 63989 66505]; x=1:10; % Analyze the trend of the company's production using a linear fit. out=GUIregress(x,y,'interpolant','linear','plots',true, 'timeseries', true); % Analyze the trend of the company's production using an exponential fit. out=GUIregress(x,y,'interpolant','exponential','plots',true,'timeseries',true); % Analyze the trend of the company's production using an power fit. out=GUIregress(x,y,'interpolant','power','plots',true,'timeseries',true)
ans =
Legend ((t,y) coordinates, Regression line (49123+1615.4545t…) with properties:
String: {1×3 cell}
Location: 'best'
Orientation: 'vertical'
FontSize: 9.00
Position: [0.15 0.85 0.16 0.06]
Units: 'normalized'
Use GET to show all properties
ans =
Legend ((t,y_t) coordinates, Exponential fit exp(10.8121+0.0…) with properties:
String: {1×3 cell}
Location: 'best'
Orientation: 'vertical'
FontSize: 9.00
Position: [0.14 0.85 0.17 0.07]
Units: 'normalized'
Use GET to show all properties
ans =
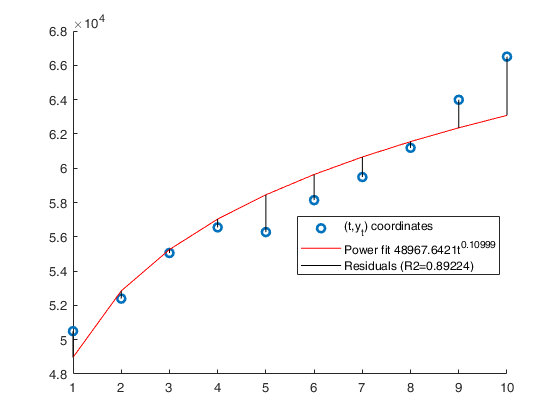
Legend ((t,y_t) coordinates, Power fit 48967.6421t^{0.10999}…) with properties:
String: {1×3 cell}
Location: 'best'
Orientation: 'vertical'
FontSize: 9.00
Position: [0.74 0.13 0.13 0.07]
Units: 'normalized'
Use GET to show all properties
out =
struct with fields:
tabledata: [11×6 table]
expa: 10.80
a: 48967.64
b: 0.11
R2: 0.89
ta: 480.54
tb: 8.14
confinta: []
confintb: []
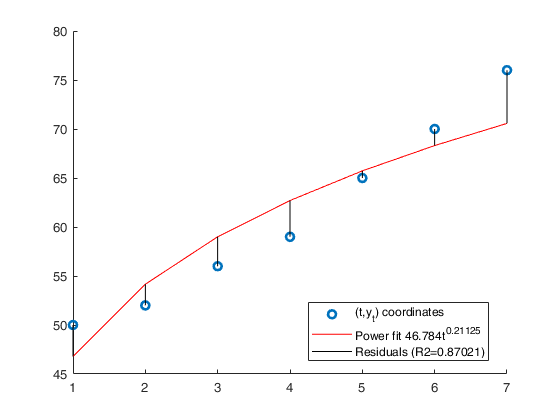
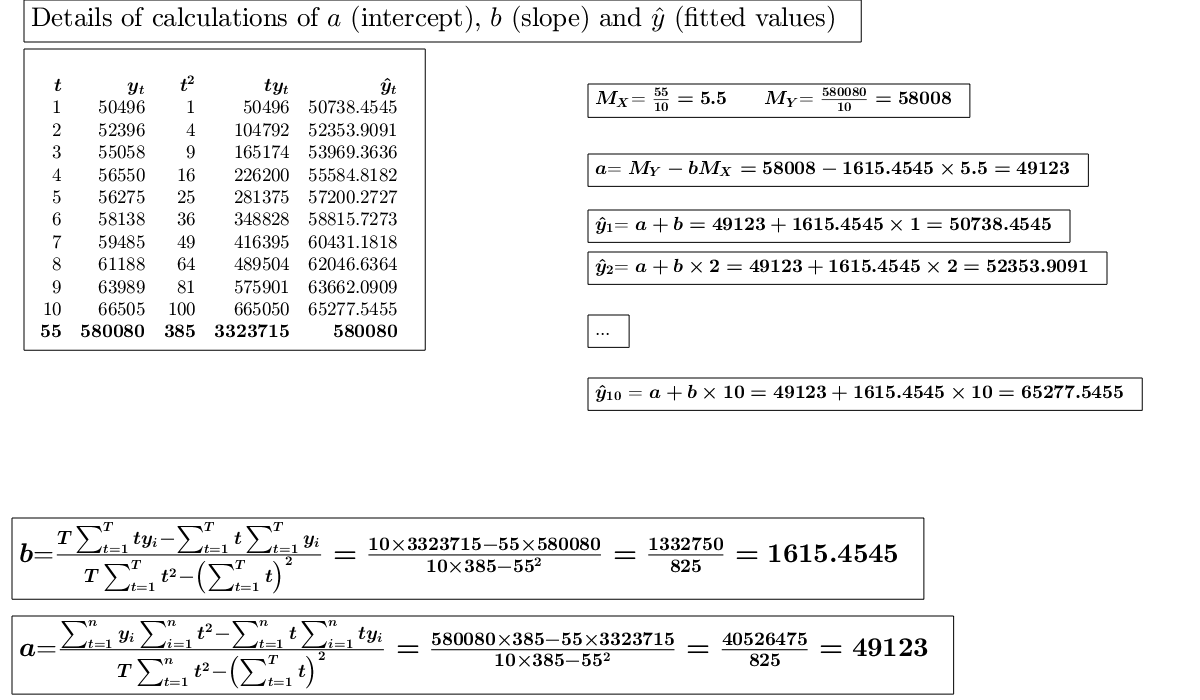
 Example of linear and power interpolation.
Example of linear and power interpolation.
 Example of linear and power interpolation.
Example of linear and power interpolation.
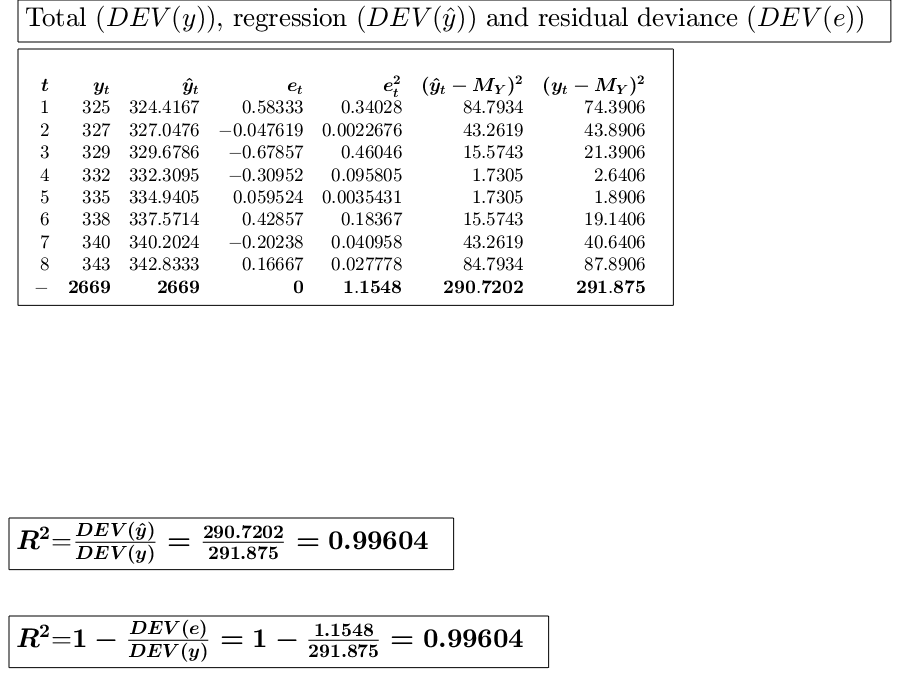
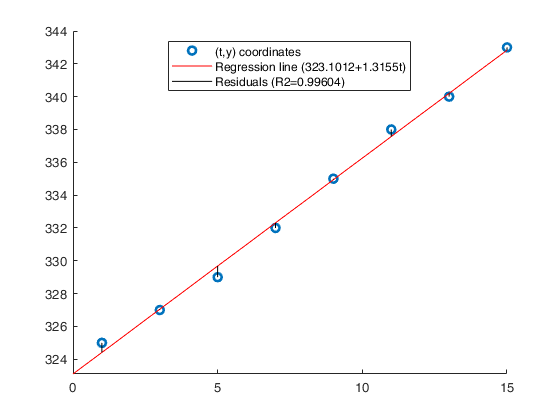
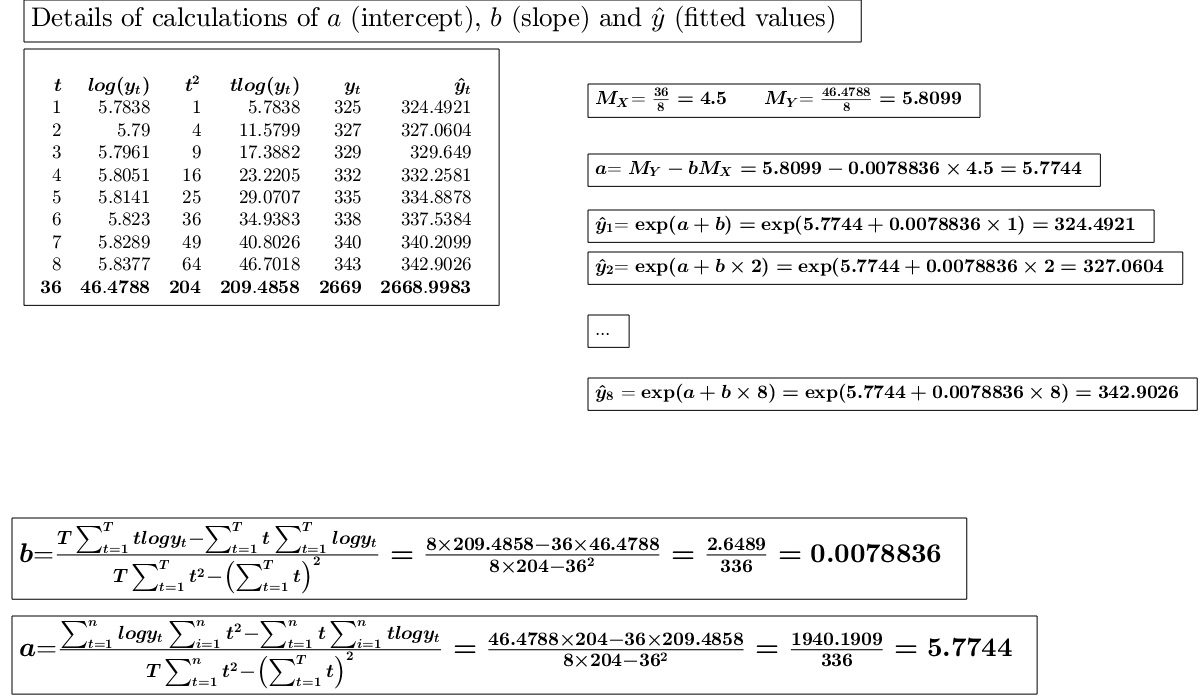
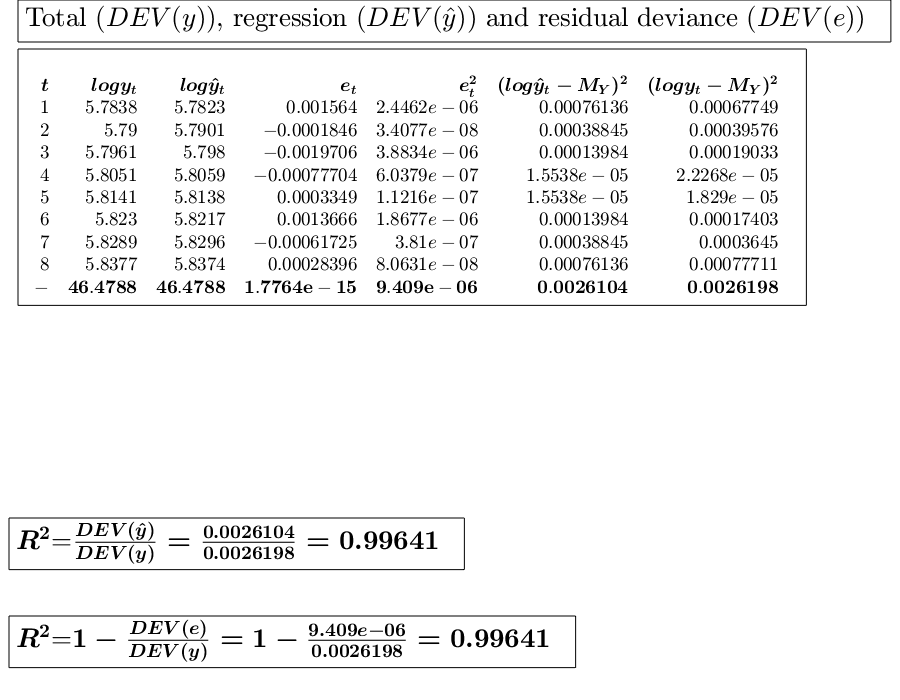
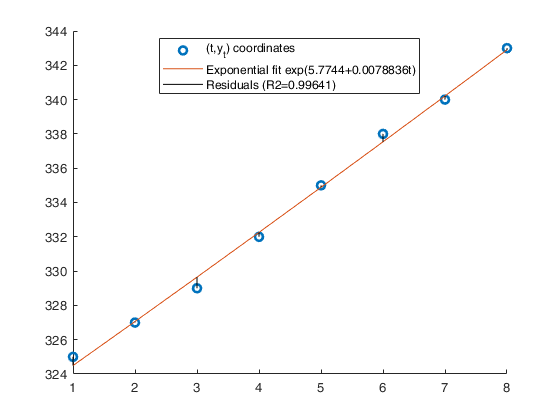
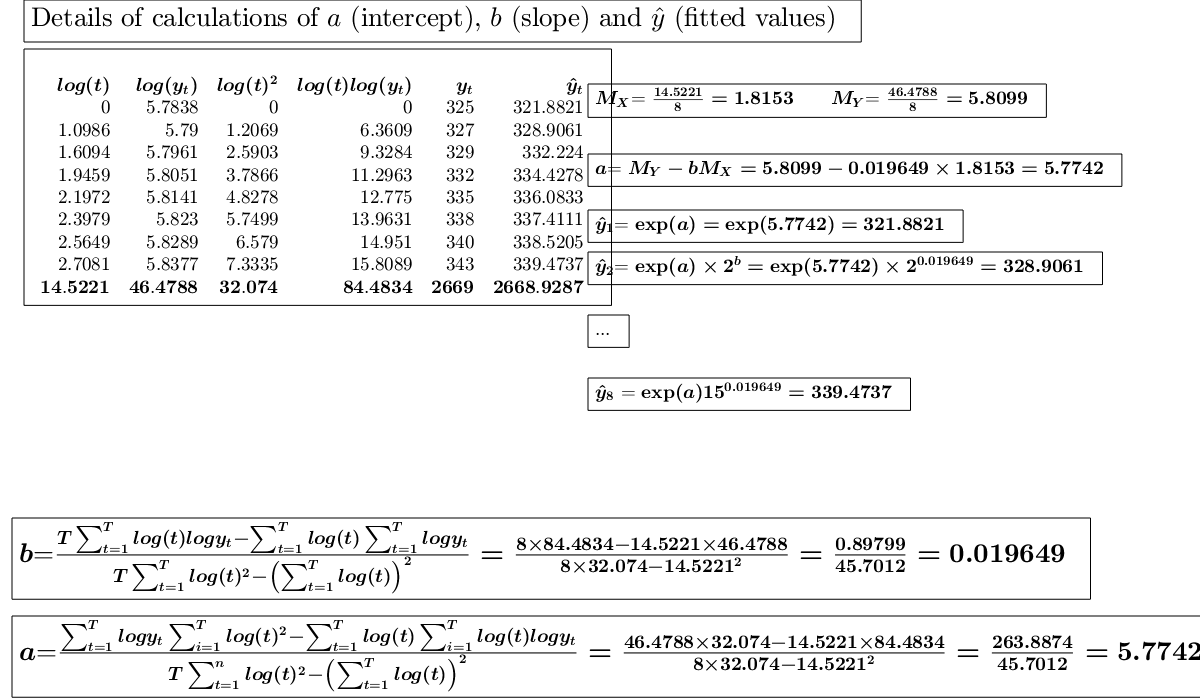
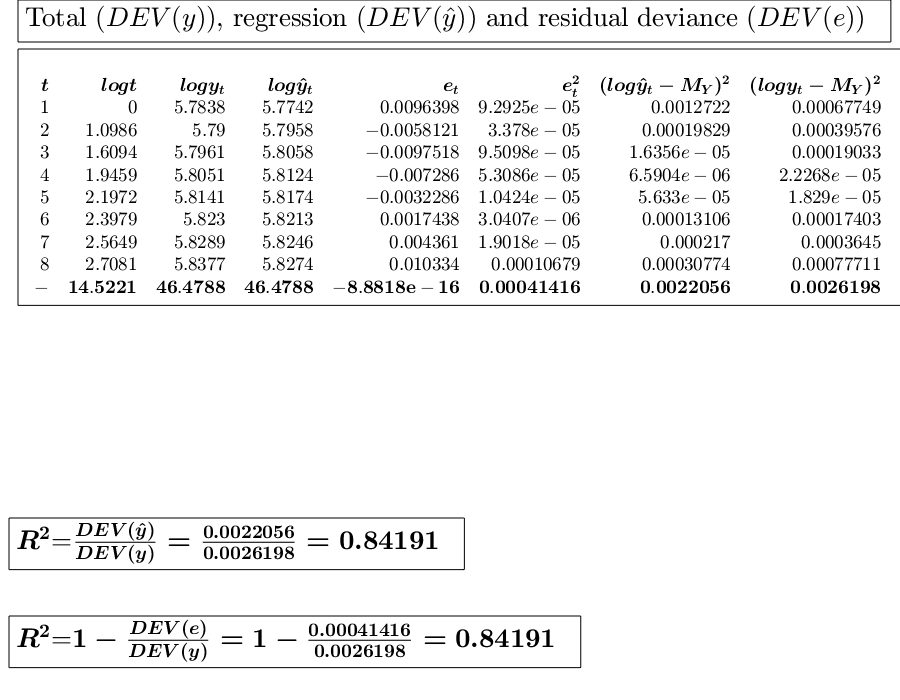
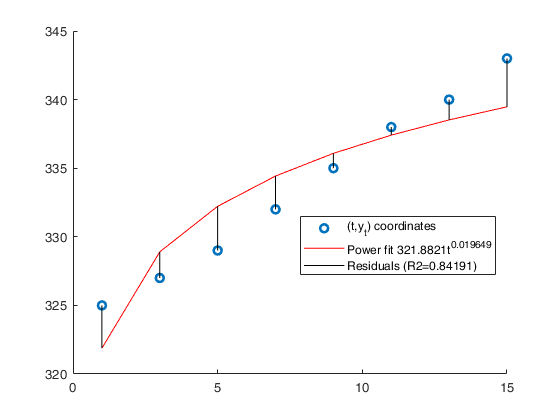
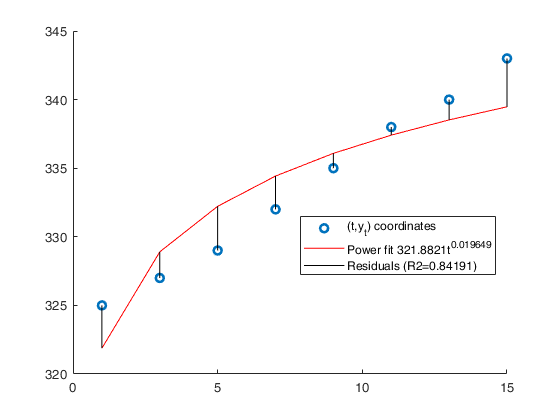
close all % Time series...., (See ex 4.26 of [CMR]) xb=1:8; xa=[1 3 5 7 9 11 13 15]; y=[325 327 329 332 335 338 340 343]; % Analyze the trend of the company's production using a linear fit. out=GUIregress(xa,y,'interpolant','linear','plots',true, 'timeseries', true); % Analyze the trend of the company's production using an exponential fit. out=GUIregress(xb,y,'interpolant','exponential','plots',true, 'timeseries', true); % Analyze the trend of the company's production using a power fit. out=GUIregress(xa,y,'interpolant','power','plots',true, 'timeseries', true);
ans =
Legend ((t,y) coordinates, Regression line (323.1012+1.3155t…) with properties:
String: {1×3 cell}
Location: 'best'
Orientation: 'vertical'
FontSize: 9.00
Position: [0.73 0.40 0.16 0.06]
Units: 'normalized'
Use GET to show all properties
ans =
Legend ((t,y_t) coordinates, Exponential fit exp(5.7744+0.00…) with properties:
String: {1×3 cell}
Location: 'best'
Orientation: 'vertical'
FontSize: 9.00
Position: [0.72 0.30 0.17 0.07]
Units: 'normalized'
Use GET to show all properties
ans =
Legend ((t,y_t) coordinates, Power fit 321.8821t^{0.019649},…) with properties:
String: {1×3 cell}
Location: 'best'
Orientation: 'vertical'
FontSize: 9.00
Position: [0.76 0.13 0.13 0.07]
Units: 'normalized'
Use GET to show all properties

 Use of option inferential.
Use of option inferential.
 Use of option inferential.
Use of option inferential.In a survey on pollution, we want to verify whether the content of a certain pollutant in the air, expressed in micrograms per cubic meter (Y) is linked to the number of manufacturing companies with more than 20 employees (X). The results obtained in some cities are given below:
x=[91 453 254 412 334 428 341 125]; y=[13 12 17 56 29 35 49 27]; out=GUIregress(x,y,'inferential',0.90,'plots',false); % There is not enough evidence to state that is not 0 in the population % and the estimated relationship between the two variables is % significant. The value of the linear index of determination % (R2=0.159) shows a very poor fit of the regression line. The % estimated model is therefore of no use for interpreting the causes of % pollution.

Input Arguments
x — vector of numeric data or table.
Vector or table or empty.
Vector containing strictly numerical data.
If x is table the second input argument y is not necessary. In this case the response is the last column of the table.
If x is empty it is assumed that regression is against time.
Data Types: double or table or []
y — vector of numeric data.
Vector containing strictly numerical data.
This input argument is not requested if previous input argument x is a table.
Data Types: double
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'inferential',0.99
, 'intercept',false
, 'timeseries', true
, 'plots',true
, 'interpolant','exponential'
inferential
—this input parameter controls whether to show an
additional GUI giving all the details for the calculation
of all the inferential aspects of the linear regression
model (i.e.
standard error of coefficients, t-statistics, p-values of the t-statistics for a two-sided test with the null hypothesis that the coefficient is zero and confidence intervals). If inferential is empty [] (default) this additional GUI is now shown. If inferential is a number in the interval (0 1), this GUI is shown and the a confidence level at inferential-per cent level is computed. For example if inferential is 0.90 a 90 per cent confidence interval is computed.
Example: 'inferential',0.99
Data Types: double or empty value
intercept
—Indicator for constant term.true (default) | false.
Indicator for the constant term (intercept) in the fit, specified as the comma-separated pair consisting of 'Intercept' and either true to include or false to remove the constant term from the regression model.
Example: 'intercept',false
Data Types: boolean
timeseries
—Flag indicating that data is a time series.false (default) | true.
Example: 'timeseries', true
Data Types: boolean
plots
—show regression graphically.boolean.
If plots is true an additional plot which shows the (x,y) data, the fitted regression line and the residuals is shown on the screen. Clicking on the line in the legend it is possible to show/hide these three components.
Example: 'plots',true
Data Types: boolean
interpolant
—interpolation method.'character'.
Possible values are 'linear' (default) for linear interpolation, 'exponential' for exponential interpolation and 'power' for power interpolation.
Example: 'interpolant','exponential'
Data Types: char
Output Arguments
out — description
Structure
Structure which contains the following fields
| Value | Description |
|---|---|
tabledata |
detailed output to compute the index. Table. Table with n+1 rows (where n is the length of x) containing what is shown in the GUI. Last row contains the totals. |
a |
intercept of linear/exponential/power regression on the original data. scalar. |
b |
slope of the of linear/exponential/power regression on the original data. scalar. |
expa |
intercept of the exponential/power regression on the transformed data. scalar. This field is present only if input option interpolant is 'exponential' or 'power'. |
expb |
slope of the exponential regression on the transformed data. scalar. This field is present only if input option interpolant is 'exponential'. |
R2 |
R squared of the regression model. scalar. When exponential/power regression is chosen, R squared is always computed on transformed data. |
ta |
t statistic for intercept. Scalar. |
tb |
t statistic for slope. Scalar. |
confinta |
confidence interval for alpha parameter. A vector of length 2 containing the extremes of confidence interval for the intercept. The default confidence level is 0.95 or it is controlled by optional input argument inferential. |
confintb |
confidence interval for alpha parameter. A vector of length 2 containing the extremes of confidence interval for the slope. The default confidence level is 0.95 or it is controlled by optional input argument inferential. |
References
Milioli, M.A., Riani, M., Zani, S. (2019), "Introduzione all'analisi dei dati statistici (Quarta edizione ampliata)". [MRZ]
Cerioli, A., Milioli, M.A., Riani, M. (2016), "Esercizi di statistica (Quinta edizione)". [CMR]
See Also
GUIvar
|
GUImad
|
GUIskewness