GUItrimmean

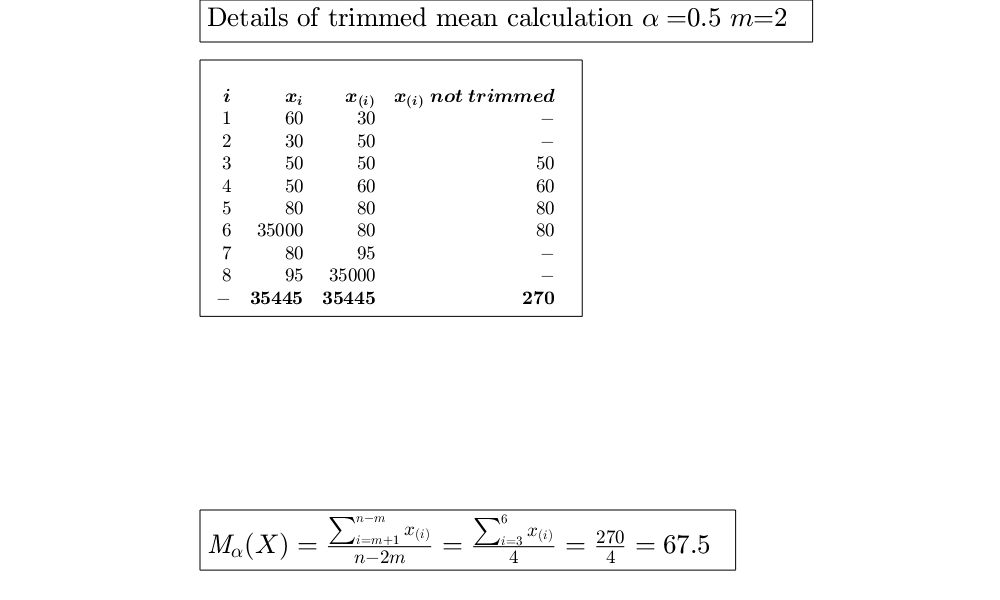
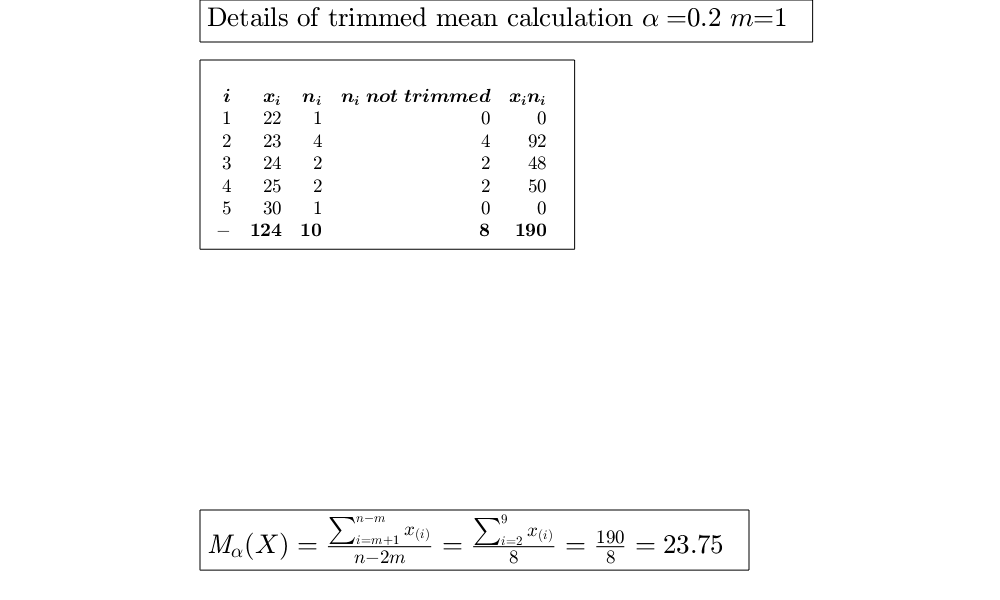
GUItrimmean shows the necessary calculations to obtain the trimmed mean in a GUI.

expand all in page

Syntax

  • out=GUItrimmean(x,percent, freq)example

Description

example

out =GUItrimmean(x, percent, freq) Use of trimmed mean with 'percent' as per cent of trimming.

Examples

expand all

  • Use of trimmed mean with 'percent' as per cent of trimming.

    • In this case we use 50% as per cent of trimming. (See page 92 of [MRZ]) 

    x=[60 30 50 50  80 35000  80 95];
out=GUItrimmean(x,50);
    Click here for the graphical output of this example (link to Ro.S.A. website).

    Related Examples

    expand all

  • Example of use of trimmed mean with 25 per cent of trimming.

    • (See page 92 of [MRZ]) 

    x=[60 30 50 50  80 35000  80 95];
out=GUItrimmean(x,25);

  • Trimmed mean in a frequency distribution.

    • Matrix X below contains the frequency distribution of the grades obtained by 10 students. (See page 71 of [CMR]) Compute the truncated mean of the grades using alpha=0.2 

    X=[22	1
25	2
30	1
23	4
24	2];
x=X(:,1);
freq=X(:,2);
GUItrimmean(x,20,freq)
    ans = 

  struct with fields:

           data: [6×5 table]
    trimmedmean: 23.7500
    Click here for the graphical output of this example (link to Ro.S.A. website)

  • Comparison of truncated mean using original data and frequency distribution.

    • % Vector x contains the temperature (Celsius degrees) in 10 places. (See page 23 of [CMR])
% Compute the truncated mean using alpha equal to 0.4.
x=[18	24	21	19 	27	12	21	15	12	16];
trimperc=40;
GUItrimmean(x,trimperc)
% Note that the same results are obtained if you use frequency
% distribution in the firsts two columns of Ta
Ta=tabulateFS(x);
GUItrimmean(Ta(:,1),trimperc,Ta(:,2))

    Input Arguments

    expand all

    x — vector of numeric data. Vector.

    Vector containing strictly numerical data.

    Data Types: double

    percent — trimming percent. Scalar.

    Percentage of input data to be trimmed specified as a scalar between 0 and 100 (generally between 0 and 50).

    For example, if x is a vector that has n values, the trimmed mean is the mean of x excluding the highest and lowest m data values, where m =[n*(percent/100)/2].

    For example if n=11 and percent=30, $n*(percent/100)/2=1.65$.

    $m=[1.65]=1$ therefore the smallest and largest observations are excluded from the computation.

    Example - 1:10

    Data Types: double

    freq — weights. Vector.

    Vector with the same length of x containing the (frequencies) weights assigned to each observation.

    Example - 1:10

    Data Types: double

    Output Arguments

    expand all

    out —detailed output to compute the index. Table

    Table with n+1 rows (where n is the length of x) containing what is shown in the GUI. Last row contains the totals.

    References

    Milioli, M.A., Riani, M., Zani, S. (2019), "Introduzione all'analisi dei dati statistici (Quarta edizione ampliata)". [MRZ]

    Cerioli, A., Milioli, M.A., Riani, M. (2016), "Esercizi di statistica (Quinta edizione)". [CMR]

    See Also

    |

    This page has been automatically generated by our routine publishFS