boxcoxR

boxcoxR finds MLE of lambda in linear regression (and confidence interval) using Box Cox, YJ or extended YJ transformation

expand all in page

Syntax

Description

The function computes the profile log Likelihood for a range of values of the transformation parameter (lambda) and computes the MLE of lambda in the supplied range. Supported families are Box Cox, Yeo and Johnson and extended Yeo and Johnson (Atkinson et al. 2020).

The profile log-likelihood is computed as:

\[ -(n/2) \log( (y(\lambda)-X\beta(\lambda))'(y(\lambda)-X\beta(\lambda))/n) +\log J \] where $y(\lambda)$ is the vector of transformed observations using Box Cox family, Yeo and Johnson or extended Yao and Johnson family \[ \beta(\lambda) = (X'X)^{-1} X' y(\lambda) \] and $J$ is the Jacobian of the transformation.

example

out =boxcoxR(y, X) boxcoxR with all default options.

example

out =boxcoxR(y, X, Name, Value) boxcoxR using YJ transformation.

Examples

expand all

  • boxcoxR with all default options.

    • Use the wool data. 

    load('wool.txt','wool');
y=wool(:,4);
X=wool(:,1:3);
out=boxcoxR(y,X);
disp(['Estimate of lambda using Box Cox is =',num2str(out.lahat)])
    Estimate of lambda using Box Cox is =-0.059

  • boxcoxR using YJ transformation.

    • load('wool.txt','wool');
y=wool(:,4);
X=wool(:,1:3);
out=boxcoxR(y,X,'family','YJ');
disp(['Estimate of lambda using YJ family is =',num2str(out.lahat)])
    Estimate of lambda using YJ family is =-0.062

    Related Examples

    expand all

  • Example of use of option confint.

    • load('wool.txt','wool');
y=wool(:,4);
X=wool(:,1:3);
% A 99.9 per cent confidence interval for lambda is used.
out=boxcoxR(y,X,'conflev',0.999);

  • Example of use of option plots.

    • load('wool.txt','wool');
y=wool(:,4);
X=wool(:,1:3);
% Plot the profile loglikelihood
out=boxcoxR(y,X,'plots',1);

  • Example of use of option plots combined with laseq.

    • load('wool.txt','wool');
y=wool(:,4);
X=wool(:,1:3);
% Plot the profile loglikelihood in the interval [-1 1]
laseq=[-1:0.0001:1];
out=boxcoxR(y,X,'plots',1,'laseq',laseq);
    Click here for the graphical output of this example (link to Ro.S.A. website)

  • Example of use of option family.

    • close all
YY=load('fondi_large.txt');
y=YY(:,2);
X=YY(:,[1 3]);
out=boxcoxR(y,X,'family','YJpn','plots',1);
% The contour plot suggests that while positive observations do not
% have to be transformed, negative observations have to be transformed using
% lambda=0. For more details see Atkinson Riani and Corbellini (2020)
    Click here for the graphical output of this example (link to Ro.S.A. website)

  • Example of the use of option usefmin.

    • rng(500)
% Generate regression data
outsim=simulateLM(100,'R2',0.95);
yori = outsim.y;
X = outsim.X;
% Transform in a different way positive and negative values
laPos=0.2;
laNeg=0.8;
y=normYJpn(yori,[],[laPos laNeg],'inverse',true);
% Use solver to find MLE of laPos and laNeg
usefmin=struct;
% specify maximum number of iterations
usefmin.MaxIter=100;
% Function boxcoxR initializes the optimization routine with the value
% of lambda from the last call of the optimization routine. This trick
% is very useful during the forward search when we use in step m+1 as
% initial guess of laP and laN the final estimate of laP and laN in
% step m.
% The instruction below clear persistent variables in function boxcoxR
clear boxcoxR
out=boxcoxR(y,X,'family','YJpn','plots',1,'usefmin',usefmin);
disp('MLE of laPos and laNeg')
disp(out.lahat)
    MLE of laPos and laNeg
    0.2364    0.8265
    Click here for the graphical output of this example (link to Ro.S.A. website)

  • Another example of the use of option usefmin.

    • In this example we specify as solver to use fminunc 

    rng(1000)
% Generate regression data
outsim=simulateLM(100,'R2',0.6);
yori = outsim.y;
X = outsim.X;
% Transform in a different way positive and negative values
laPos=0.4;
laNeg=-0.9;
y=normYJpn(yori,[],[laPos laNeg],'inverse',true);
% Use solver to find MLE of laPos and laNeg
usefmin=struct;
% specify maximum number of iterations
usefmin.MaxIter=100;
% Note that to specify as solver fminunc the optimization toolbox is
% needed.
usefmin.solver='fminunc';
out=boxcoxR(y,X,'family','YJpn','plots',1,'usefmin',usefmin);
disp('MLE of laPos and laNeg')
disp(out.lahat)
% Check that the values after the optimization are as expected
assert(max(abs(out.lahat-[0.3166   -0.8825]))<1e-4,'Wrong values of laP and laN')
    MLE of laPos and laNeg
    0.3166   -0.8825

  • Example using simulated contaminated data.

    • rng(10000)
% Generate X and y data
n=200;
X=randn(n,3);
beta=[ 1; 1; 1];
sig=0.5;
ytrue=X*beta+sig*randn(n,1);
% Contaminate response
ycont=ytrue;
ycont(21:40)=ycont(21:40)+4;
% Use two different values for laP and laN
lapos=0.5;
laneg=0;
ytra=normYJpn(ytrue,[],[lapos laneg],'inverse',true,'Jacobian',false);
yconttra=normYJpn(ycont,[],[lapos laneg],'inverse',true,'Jacobian',false);
% In this example the true values of laP and laN are 0.5 and 0 however due
% to contamination the MLE of lambda laP because very close to 0.
% This wrongly suggests a unique value of lambda.
subplot(2,1,1)
out=boxcoxR(ytra,X,'family','YJpn','plots',1);
subplot(2,1,2)
outcont=boxcoxR(yconttra,X,'family','YJpn','plots',1);
    Click here for the graphical output of this example (link to Ro.S.A. website)

    Input Arguments

    expand all

    y — Response variable. Vector.

    Response variable, specified as a vector of length n, where n is the number of observations. Each element of y is the response for the corresponding row of X.

    Missing values (NaN's) and infinite values (Inf's) are allowed, but observations (rows) with these values will automatically be excluded from the computations.

    Data Types: single| double

    X — Predictor variables. Matrix.

    Matrix of explanatory variables (also called 'regressors') of dimension n x (p-1) where p denotes the number of explanatory variables including the intercept.

    Rows of X represent observations, and columns represent variables. By default, there is a constant term in the model, unless it is explicitly removed using input option intercept; so, do not include a column of 1s in X. Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with such values will automatically be excluded from the computations.

    Data Types: single| double

    Name-Value Pair Arguments

    Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

    Example: 'intercept',false , 'family','YJ' , 'nocheck',true , 'conflev',0.99 , 'laseq',[-1:0.001;0.7] , 'laseqPos',[-1:0.001;0.7] , 'laseqNeg',[-1:0.001;0.7] , 'plots',true , 'usefmin',true

    intercept —Indicator for constant term.true (default) | false.

    Indicator for the constant term (intercept) in the fit, specified as comma-separated pair consisting of 'Intercept' and either true or false, to respectively include or remove the constant term from the model.

    Example: 'intercept',false

    Data Types: boolean

    family —parametric transformation to use.string.

    String which identifies the family of transformations which must be used. Character. Possible values are 'BoxCox' (default), 'YJ' (Yao and Yohnson) and 'YJpn' (extended Yeo and Johnson).

    The Box-Cox family of power transformations equals $(y^{\lambda}-1)/\lambda$ for $\lambda$ not equal to zero, and $\log(y)$ if $\lambda = 0$.

    The Yeo-Johnson (YJ) transformation is the Box-Cox transformation of $y+1$ for nonnegative values, and of $|y|+1$ with parameter 2-lambda for y negative.

    The extended Yeo-Johnson (YJpn) transformation is like Yeo-Johnson, but admits two values of the transformation parameters, respectively for positive and negative observations.

    Remark. BoxCox family can be used only if input y is positive. Yeo-Johnson (and extended Yeo-Johnson family of transformations do not have this limitation).

    Example: 'family','YJ'

    Data Types: char

    nocheck —Check input arguments.boolean.

    If nocheck is equal to true no check is performed on vector y and matrix X. This means that y and X are left unchanged. Note also that the additional column of ones for the intercept is not added.

    As default nocheck=false.

    Example: 'nocheck',true

    Data Types: boolean

    conflev —Confidence level for lambda.scalar.

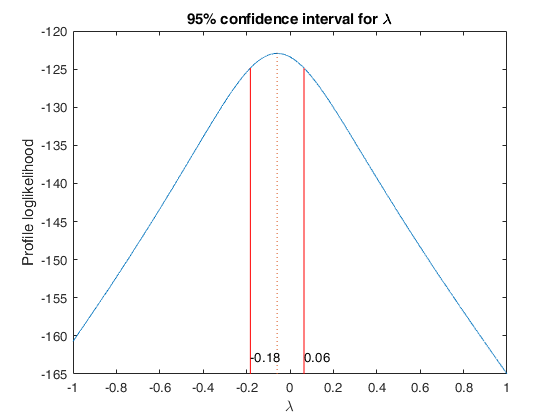
    The scalar is between 0 and 1 and determines the confidence level for lambda, based on the asymptotic $chi1^2$ of twice the loglikelihood ratio. The default conflev value is 0.95;

    Example: 'conflev',0.99

    Data Types: double

    laseq —Sequence of values of lambda to consider.vector.

    Vector which contains the sequence of values of lambda for which the profile loglikelihood has to be computed if family is 'BoxCox' or 'YJ'. The default value of laseq is -2:0.001:2. This optional input is ignored if family is 'YJpn';

    Example: 'laseq',[-1:0.001;0.7]

    Data Types: double

    laseqPos —Transformation for positive observations.vector.

    Vector which contains the sequence of values of lambda which are used to transform positive observations when family 'YJpn'. The default value of laseqPos is -2:0.01:2. This optional input parameter is ignored if family is 'BoxCox' or 'YJ';

    Example: 'laseqPos',[-1:0.001;0.7]

    Data Types: double

    laseqNeg —Transformation for negative observations.vector.

    Vector which contains the sequence of values of lambda which are used to transform negative observations when family 'YJpn'. The default value of laseqNeg is -2:0.01:2. This optional input is ignored if family is 'BoxCox' or 'YJ';

    Example: 'laseqNeg',[-1:0.001;0.7]

    Data Types: double

    plots —Profile log likelihood for lambda.boolean.

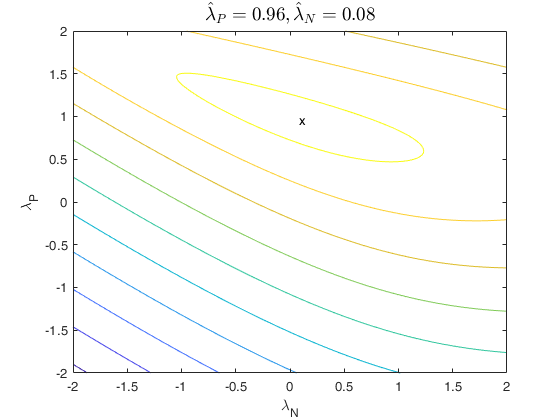
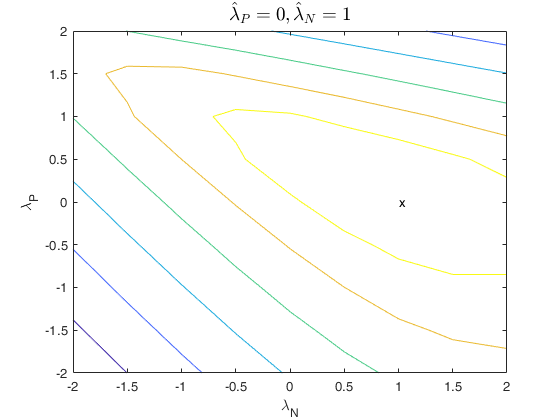
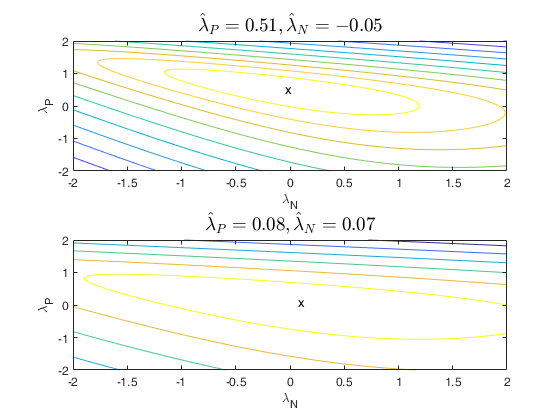
    It specifies whether to show the profile log likelihood of lambda. If plots is true, the plot of the profile loglikelihood is produced together with the requested confidence interval. The default value of prolik is false, that is no plot is produced. If family is 'YJpn', a contour plot is produced.

    Example: 'plots',true

    Data Types: boolean

    usefmin —use solver to find MLE of lambda.boolean | struct.

    This option applies only if family is YJpn. If usefmin is true or usefmin is a struct, the maximum likelihood estimates of $\lambda_P$ and $\lambda_N$ is computed using the MATLAB solvers fminsearch or fminunc. The default value of usefmin is false, that is the likelihood is evaluated at the points laseqPos and laseqNeg without the solver.

    If usefmin is a structure it may contain the following fields:

    Value Description
    MaxIter

    Maximum number of iterations (default is 1000).
    TolX

    Termination tolerance for the parameters (default is 1e-7).
    solver

    name of the solver. Possible values are 'fminsearch' (default) and 'fminunc'. fminunc needs the optimization toolbox.
    displayLevel

    amount of information displayed by the algorithm. possible values are 'off' (displays no information, this is the default), 'final' (displays just the final output) and 'iter' (displays iterative output to the command window).

    Example: 'usefmin',true

    Data Types: boolean or struct

    Output Arguments

    expand all

    out — description Structure

    Structure which contains the following fields

    Value Description
    lahat

    best estimate of lambda. Scalar or vector of length 2.

    out.lahat is a scalar if family is 'BoxCox' or 'YJ', otherwise if family is 'YJpn' it is a vector of length 2 containing respectively MLE of transformation parameter for positive and negative observations. This is the best estimate among the values of lambda which are supplied in input vector laseq if family is 'BoxCox' or 'YJ', or in input vectors laseqPos and laseqNeg, if family is 'YJpn'.
    lahatci

    confidence intervals for MLE of lambda computed using Chi2 approximation using confidence level specified in input option conflev. This argument is present only if family is 'BoxCox' or 'YJ'.
    LogLik

    matrix containing the value of the profile log-likelihood for each value in laseq or laseqPos and laseqNeg. If family is BoxCox' or 'YJ', the dimension of out.LogLik is length(laseq)-by-2. In this case the first column contains the values of laseq and the second column the values of the profile log likelihood. If family is 'YJpn', the dimension of out.LogLik is: * length(laseqPos)-by-length(laseqNeg) if option usefmin is false (default) and therefore the maximization routine is not called.

    * 9-by-9 matrix containing the value of the likelihood in correspondence of the points -2:0.5:2, if input option usefmin is true and boxcoxR is called for the first time.

    In order to find MLE of laPos and laNeg, the likelihood is computed for the 81 values in the meshgrid -2:0.5:2 to find a preliminary estimate of laPos and laNeg for the solver.

    * empty value if input option usefmin is true and the solver has used the cached version of lambda to initialize the optimization routine. If you prefer that the maximization routine does not use the cached version of lambda, execute instruction clear boxcoxR before calling it.
    exitflag

    flag which informs about convergence. exitflag = 0 implies normal convergence, else no convergence has been obtained. This output is present only if input option usefmin is true or struct and family is YJpn.

    References

    Atkinson, A.C. and Riani, M. (2000), "Robust Diagnostic Regression Analysis", Springer Verlag, New York. [see pp. 83-84]

    Box, G.E.P. and Cox, D.R. (1964), An analysis of transformations (with Discussion), "Journal of the Royal Statistical Society Series B", Vol. 26, pp. 211-252.

    Yeo, I.K and Johnson, R. (2000), A new family of power transformations to improve normality or symmetry, "Biometrika", Vol. 87, pp. 954-959.

    Atkinson, A.C., Riani, M. and Corbellini C. (2019), The Analysis of Transformations for Profit and Loss Data, "Journal of the Royal Statistical Society. Series C: Applied Statistics", https://doi.org/10.1111/rssc.12389 [ARC]

    Atkinson, A.C. Riani, M. and Corbellini A. (2021), The Box–Cox Transformation: Review and Extensions, "Statistical Science", Vol. 36, pp. 239-255, https://doi.org/10.1214/20-STS778

    Acknowledgements

    This function has been inspired by submission https://www.mathworks.com/matlabcentral/fileexchange/10419-box-cox-power-transformation-for-linear-models in the file exchange written by Hovav Dror, hovav@hotmail.com, March 2006

    See Also

    |

    This page has been automatically generated by our routine publishFS