FSRfan
FSRfan monitors the values of the score test statistic for each lambda
Description
The transformations for negative and positive responses were determined by Yeo and Johnson (2000) by imposing the smoothness condition that the second derivative of zYJ(λ) with respect to y be smooth at y = 0.
However,some authors, for example Weisberg (2005), query the physical interpretability of this constraint, which is often violated in data analysis. Accordingly, Atkinson et al (2019) and (2020) extend the Yeo-Johnson transformation to allow two values of the transformations parameter: \lambda_N for negative observations and \lambda_P for non-negative ones.
FSRfan monitors: 1) the t test associated with the constructed variable computed assuming the same transformation parameter for positive and negative observations fixed. In short we call this test, "global score test for positive observations".
2) the t test associated with the constructed variable computed assuming a different transformation for positive observations keeping the value of the transformation parameter for negative observations fixed. In short we call this test, "test for positive observations".
3) the t test associated with the constructed variable computed assuming a different transformation for negative observations keeping the value of the transformation parameter for positive observations fixed. In short we call this test, "test for negative observations".
4) the F test for the joint presence of the two constructed variables described in points 2) and 3.
4) the F likelihood ratio test based on the MLE of \lambda_P and \lambda_N. In this case, the residual sum of squares of the null model based on a single transformation parameter \lambda is compared with the residual sum of squares of the model based on data transformed data using MLE of \lambda_P and \lambda_N.
FSRfan with optional arguments.out
=FSRfan(y,
X,
Name, Value)
Examples
 FSRfan with all default options.
FSRfan with all default options.
 FSRfan with all default options.
FSRfan with all default options.Store values of the score test statistic for the five most common values of \lambda.
% Produce also a fan plot and display it on the screen.
% Common part to all examples: load wool dataset.
XX=load('wool.txt');
y=XX(:,end);
X=XX(:,1:end-1);
% Function FSRfan stores the score test statistic.
% In this case we use the five most common values of lambda are considered
[out]=FSRfan(y,X);
fanplotFS(out);
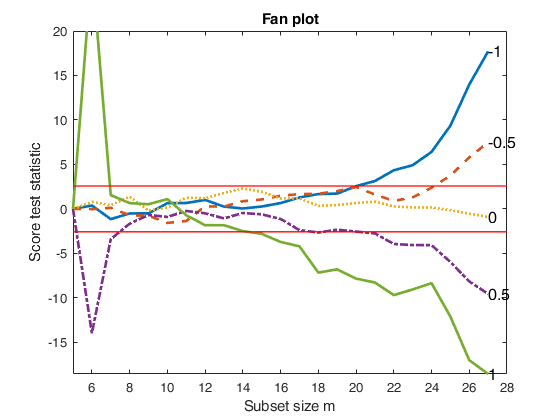
%The fan plot shows the log transformation is diffused throughout the data and does not depend on the presence of particular observations.
Total estimated time to complete LMS: 0.01 seconds ------------------------------ Warning: Number of subsets without full rank equal to 15.7% Total estimated time to complete LMS: 0.00 seconds ------------------------------ Warning: Number of subsets without full rank equal to 15.7% Total estimated time to complete LMS: 0.00 seconds ------------------------------ Warning: Number of subsets without full rank equal to 15.7% Total estimated time to complete LMS: 0.00 seconds ------------------------------ Warning: Number of subsets without full rank equal to 15.7% Total estimated time to complete LMS: 0.00 seconds ------------------------------ Warning: Number of subsets without full rank equal to 15.7%
FSRfan with optional arguments.
Produce a personalized fan plot with required font sizes for labels and axes.
XX=load('wool.txt');
y=XX(:,end);
X=XX(:,1:end-1);
[out]=FSRfan(y,X,'plots',1,'FontSize',16,'SizeAxesNum',16);
Related Examples
Example specifying \lambda.
Produce a fan plot for each value of \lambda inside vector la.
% Extract in matrix Un the units which entered the search in each step
XX=load('wool.txt');
y=XX(:,end);
X=XX(:,1:end-1);
la=[-1 -0.5 0 0.5];
[out]=FSRfan(y,X,'la',la,'plots',1);
Unsel=cell2mat(out.Un);
lla=length(la);
nr=size(Unsel,1)/lla;
Un=[Unsel(1:nr,1) reshape(Unsel(:,2),nr,lla)];
Example specifying the confidence level and the initial
starting point for monitoring.
% Construct fan plot specifying the confidence level and the initial
% starting point for monitoring.
XX=load('wool.txt');
y=XX(:,end);
X=XX(:,1:end-1);
[out]=FSRfan(y,X,'init',size(X,2)+2,'nsamp',0,'conflev',0.95,'plots',1);
Example with starting point based on LTS.
Extraction of all subsamples, construct fan plot specifying the confidence level and the initial starting point for monitoring based on p+2 observations strong line width for lines associated with the confidence bands.
XX=load('wool.txt');
y=XX(:,end);
X=XX(:,1:end-1);
[out]=FSRfan(y,X,'init',size(X,2)+2,'nsamp',0,'lms',0,'lwdenv',3,'plots',1);
 Fan plot using fidelity cards data.
Fan plot using fidelity cards data.
 Fan plot using fidelity cards data.
Fan plot using fidelity cards data.In the example, la is the vector containing the most common values of the transformation parameter.
% Store the score test statistics for the specified values of lambda
% and automatically produce the fan plot
XX=load('loyalty.txt');
namey='Sales'
y=XX(:,end);
nameX={'Number of visits', 'Age', 'Number of persons in the family'};
X=XX(:,1:end-1);
% la = vector containing the most common values of the transformation
% parameter
la=[0 1/3 0.4 0.5];
% Store the score test statistics for the specified values of lambda
% and automatically produce the fan plot
[out]=FSRfan(y,X,'la',la,'init',size(X,2)+2,'plots',1,'lwd',3);
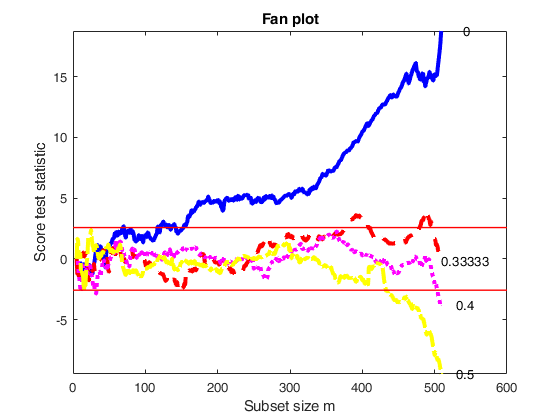
% The fan plot shows that even if the third root is the best value of the
% transformation parameter at the end of the search, in earlier steps it
% lies very close to the upper rejection region. The best value of the
% transformation parameter seems to be the one associated with l=0.4,
% which is always the confidence bands, but at the end of search, due to
% the presence of particular observations, it goes below the lower
% rejection line.
namey =
'Sales'
Total estimated time to complete LMS: 0.01 seconds
Total estimated time to complete LMS: 0.02 seconds
Total estimated time to complete LMS: 0.03 seconds
Total estimated time to complete LMS: 0.02 seconds
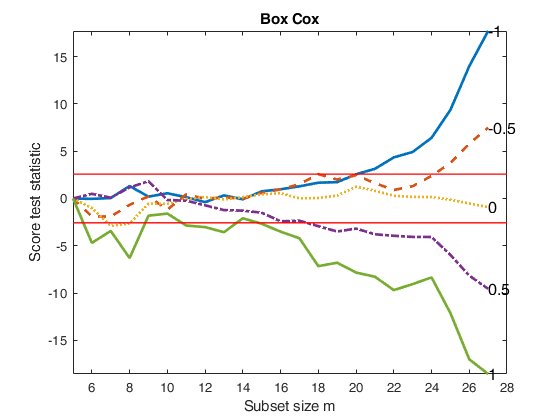
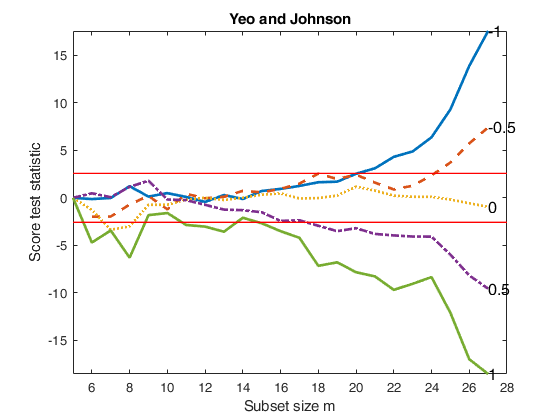
 Compare BoxCox with Yeo and Johnson transformation.
Compare BoxCox with Yeo and Johnson transformation.
 Compare BoxCox with Yeo and Johnson transformation.
Compare BoxCox with Yeo and Johnson transformation.Store values of the score test statistic for the five most common values of \lambda.
% Produce also a fan plot and display it on the screen.
% Common part to all examples: load wool dataset.
XX=load('wool.txt');
y=XX(:,end);
X=XX(:,1:end-1);
% Store the score test statistic using Box Cox transformation.
[outBC]=FSRfan(y,X,'nsamp',0);
% Store the score test statistic using Yeo and Johnson transformation.
[outYJ]=FSRfan(y,X,'family','YJ','nsamp',0);
fanplotFS(outBC,'titl','Box Cox');
fanplotFS(outYJ,'titl','Yeo and Johnson','tag','YJ');
disp('Maximum difference in absolute value')
disp(max(max(abs(outYJ.Score-outBC.Score))))
Total estimated time to complete LMS: 0.04 seconds
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
Total estimated time to complete LMS: 0.04 seconds
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
Total estimated time to complete LMS: 0.04 seconds
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
Total estimated time to complete LMS: 0.04 seconds
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
Total estimated time to complete LMS: 0.04 seconds
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
Total estimated time to complete LMS: 0.04 seconds
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
Total estimated time to complete LMS: 0.04 seconds
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
Total estimated time to complete LMS: 0.04 seconds
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
Total estimated time to complete LMS: 0.04 seconds
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
Total estimated time to complete LMS: 0.04 seconds
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
Maximum difference in absolute value
0.7564
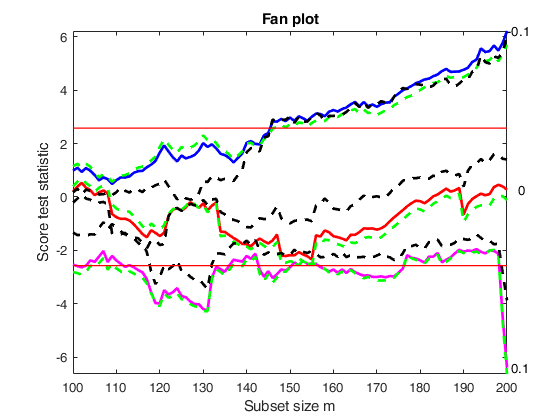
 Example of monitoring of score test for positive and negative observations.
Example of monitoring of score test for positive and negative observations.
 Example of monitoring of score test for positive and negative observations.
Example of monitoring of score test for positive and negative observations.
rng('default')
rng(10)
close all
n=200;
X=randn(n,3);
beta=[ 1; 1; 1];
sig=0.5;
y=X*beta+sig*randn(n,1);
disp('Fit in the true scale')
disp('R2 of the model in the true scale')
if verLessThanFS('8.1')
out=regstats(y,X,'linear',{'rsquare'});
disp(out.rsquare)
else
outlmori=fitlm(X,y);
disp(outlmori.Rsquared.Ordinary)
end
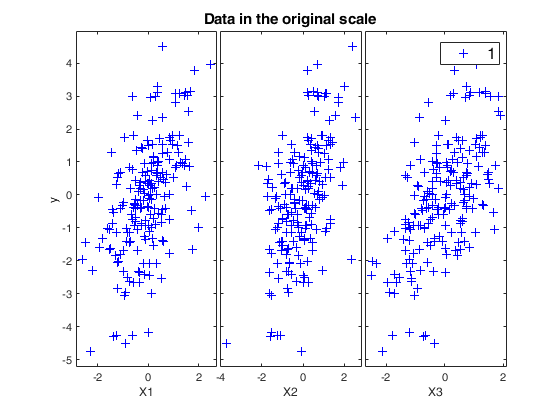
[~,~,BigAx]=yXplot(y,X,'tag','ori');
title(BigAx,'Data in the original scale')
% Find the data to transform
la=-0.25;
ytra=normYJ(y,[],la,'inverse',true);
if any(isnan(ytra))
disp('response with missing values')
end
disp('Fit in the transformed scale')
disp('R2 of the model in the wrong (inverse) scale')
if verLessThanFS('8.1')
out=regstats(ytra,X,'linear',{'rsquare'});
disp(out.rsquare)
else
outlmtra=fitlm(X,ytra);
disp(outlmtra.Rsquared.Ordinary)
end
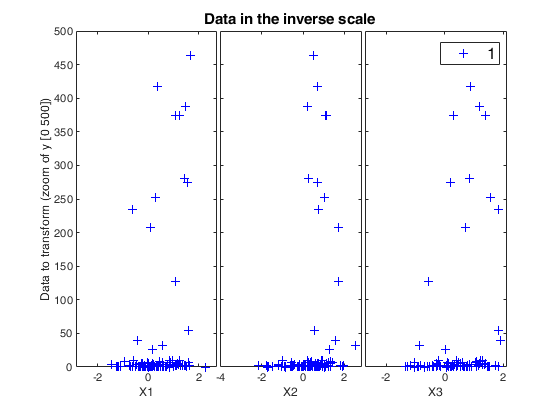
[~,~,BigAx]=yXplot(ytra,X,'tag','tra','namey','Data to transform (zoom of y [0 500])','ylimy',[0 500]);
title(BigAx,'Data in the inverse scale')
la=[ -0.5 -0.25 0];
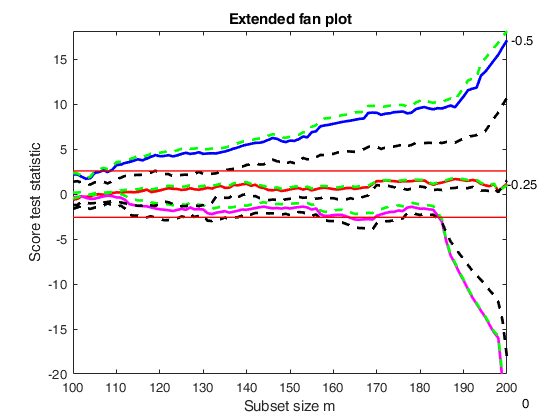
out=FSRfan(ytra,X,'la',la,'family','YJpn','plots',1,'init',round(n/2),'msg',0);
title('Extended fan plot')
Fit in the true scale
R2 of the model in the true scale
0.8993
Fit in the transformed scale
R2 of the model in the wrong (inverse) scale
0.0471
 Example of monitoring all score tests (also the F test).
Example of monitoring all score tests (also the F test).
 Example of monitoring all score tests (also the F test).
Example of monitoring all score tests (also the F test).
rng('default')
rng(1000)
close all
n=200;
X=randn(n,3);
beta=[ 1; 1; 1];
sig=0.5;
y=X*beta+sig*randn(n,1);
% Find the data to transform
la=0;
ytra=normYJ(y,[],la,'inverse',true);
if any(isnan(ytra))
disp('response with missing values')
end
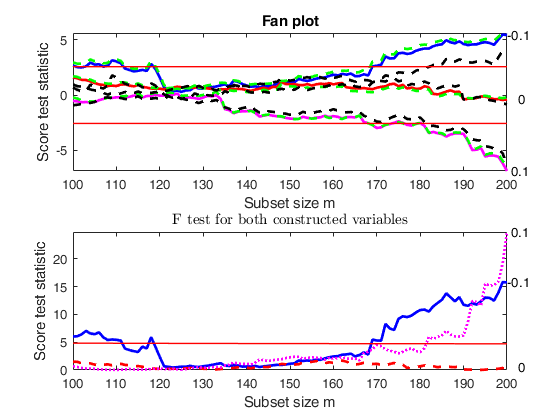
la=[ -0.1 0 0.1];
% In this case family is YJall
out=FSRfan(ytra,X,'la',la,'family','YJall','plots',1,'init',round(n/2),'msg',0);
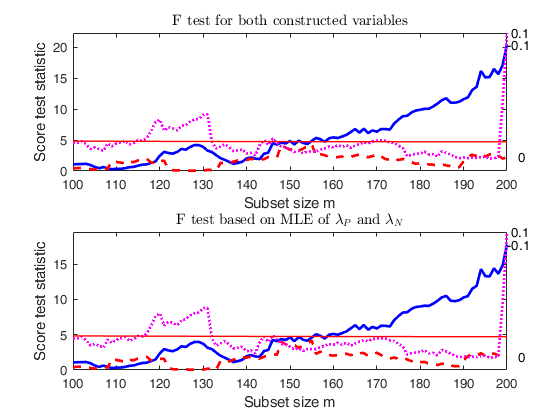
 Comparison of F test based on constructed variables with F test based on MLE.
Comparison of F test based on constructed variables with F test based on MLE.
 Comparison of F test based on constructed variables with F test based on MLE.
Comparison of F test based on constructed variables with F test based on MLE.
rng('default')
rng(100)
close all
n=200;
X=randn(n,3);
beta=[ 1; 1; 1];
sig=0.5;
y=X*beta+sig*randn(n,1);
% Find the data to transform
la=0;
ytra=normYJ(y,[],la,'inverse',true);
if any(isnan(ytra))
disp('response with missing values')
end
la=[ -0.1 0 0.1];
% Monitor test based on MLE using option scoremle
scoremle= true;
out=FSRfan(ytra,X,'la',la,'family','YJall','plots',1,'init',round(n/2),'msg',false,'scoremle',true);
Input Arguments
y — Response variable.
Vector.
A vector with n elements that contains the response variable. It can be either a row or a column vector.
Data Types: single| double
X — Predictor variables.
Matrix.
Data matrix of explanatory variables (also called 'regressors') of dimension (n x p-1). Rows of X represent observations, and columns represent variables. Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations. NOTICE THAT THE INTERCEPT MUST ALWAYS BE INCLUDED.
Data Types: single| double
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'family','YJ'
, 'h',5
, 'init',100 starts monitoring from step m=100
, 'intercept',false
, 'la',[-1 -0.5]
, 'lms',1
, 'msg',false
, 'nocheck',true
, 'nsamp',1000
, 'scoremle',true
, 'tukey1df',true
, 'usefmin',true
, 'plots',1
, 'conflev',[0.9 0.95 0.99]
, 'FontSize',20
, 'labx','my labx'
, 'laby','my laby'
, 'lwd',5
, 'lwdenv',5
, 'SizeAxesNum',12
, 'titl','my title'
, 'xlimx',[0 1]
, 'ylimy',[0 1]
family
—string which identifies the family of transformations which
must be used.character.
Possible values are 'BoxCox' (default), 'YJ', 'YJpn' or 'YJall'.
The Box-Cox family of power transformations equals (y^{\lambda}-1)/\lambda for \lambda not equal to zero, and \log(y) if \lambda = 0.
The Yeo-Johnson (YJ) transformation is the Box-Cox transformation of y+1 for nonnegative values, and of |y|+1 with parameter 2-\lambda for y negative.
Remember that BoxCox can be used just if input y is positive. Yeo-Johnson family of transformations does not have this limitation.
If family is 'YJpn', Yeo-Johnson family is applied, but in this case it is also possible to monitor (in the output arguments out.Scorep and out.Scoren) the score test respectively for positive and negative observations.
If family is 'YJall', it is also possible to monitor the joint F test for the presence of the two constructed variables for positive and negative observations.
Example: 'family','YJ'
Data Types: char
h
—The number of observations that have determined the
least trimmed (median of) squares estimator.integer.
Generally h is an integer greater or equal than [(n+size(X,2)+1)/2] but smaller then n
Example: 'h',5
Data Types: double
init
—Search initialization.scalar.
It specifies the initial subset size to start monitoring the value of the score test, if init is not specified it will be set equal to: p+1, if the sample size is smaller than 40;
min(3*p+1,floor(0.5*(n+p+1))), otherwise.
Example: 'init',100 starts monitoring from step m=100
Data Types: double
intercept
—Indicator for constant term.true (default) | false.
Indicator for the constant term (intercept) in the fit, specified as the comma-separated pair consisting of 'Intercept' and either true to include or false to remove the constant term from the model.
Example: 'intercept',false
Data Types: boolean
la
—values of the transformation parameter for which it is
necessary to compute the score test.vector.
Default value of lambda is la=[-1 -0.5 0 0.5 1]; that is the five most common values of lambda
Example: 'la',[-1 -0.5]
Data Types: double
lms
—Criterion to use to find the initial
subset to initialize the search.scalar | Vector.
If lms=1 (default) Least Median of Squares is computed, else Least trimmed of Squares is computed.
If lms is matrix with size p-1+intercept-by-length(la), it contains in column j=1,..., length(la) the list of units forming the initial subset for the search associated with la(j). In this last case previous input option nsamp is ignored.
Example: 'lms',1
Data Types: double
msg
—Level of output to display.boolean.
Boolean scalar which controls whether to display or not messages on the screen.
If msg==true (default) messages are displayed on the screen about estimated time to compute the LMS (LTS) for each value of lambda else no message is displayed on the screen
Example: 'msg',false
Data Types: logical
nocheck
—Check input arguments.boolean.
If nocheck is equal to true no check is performed on matrix y and matrix X. Notice that y and X are left unchanged. In other words the additional column of ones for the intercept is not added. As default nocheck=false.
Example: 'nocheck',true
Data Types: boolean
nsamp
—Number of subsamples which will be extracted to find
the robust estimator.scalar.
If nsamp=0 all subsets will be extracted. They will be (n choose p). Remark: if the number of all possible subset is <1000, the default is to extract all subsets otherwise just 1000. If nsamp is a matrix of size r-by-p, it contains in the rows the subsets which sill have to be extracted. For example, if p=3 and nsamp=[ 2 4 9; 23 45 49; 90 34 1]; the first subset is made up of units [2 4 9], the second subset of units [23 45 49] and the third subset of units [90 34 1];
Example: 'nsamp',1000
Data Types: double
scoremle
—likelihood ratio test for the two different transformation
parameters \lambda_P and \lambda_N.boolean.
If scoremle is true it is possible to compute the likelihood ratio test. In this case the residual sum of squares of the null model based on a single transformation parameter \lambda is compared with the residual sum of squares of the model based on data transformed data using MLE of \lambda_P and \lambda_N. If scoremle is true it is possible through following option usefmin, to control the parameters of the optimization routine.
Example: 'scoremle',true
Data Types: logical
tukey1df
—Tukey's one df test.boolean.
Tukey's one degree of freedome test for non-additivity.
The constructed variable is given by
w_T(\lambda)= (\hat z(\lambda) - \overline z(\lambda))^2 / 2 \overline z(\lambda)where z(\lambda) is the transformed response, and \hat z(\lambda) are the fitted values on the transformed response. The t test on the constructed variable above provides a test from departures from the assumed linear model and is known in the literature as Tukey's one degree of freedome test for non-additivity.
If tukey1df is true the test is computed and returned inside output structure with fieldname ScoreT else (default) the value of the test is not computed.
Example: 'tukey1df',true
Data Types: boolean
usefmin
—use solver to find MLE of lambda.boolean | struct.
This option takes effect only when input option 'family' is 'YJpn' or 'YJall'. If usefmin is true or usefmin is a struct, it is possible to use MATLAB solvers fminsearch or fminunc to find the maximum likelihood estimates of \lambda_P and \lambda_N. The default value of usefmin is false that is solver is not used and the likelihood is evaluated at the grid of points with steps 0.01.
If usefmin is a structure it may contain the following fields:
| Value | Description |
|---|---|
MaxIter |
Maximum number of iterations (default is 1000). |
TolX |
Termination tolerance for the parameters (default is 1e-7). |
solver |
name of the solver. Possible values are 'fminsearch' (default) and 'fminunc'. fminunc needs the optimization toolbox. |
displayLevel |
amount of information displayed by the algorithm. Possible values are 'off' (displays no information, this is the default), 'final' (displays just the final output) and 'iter' (displays iterative output to the command window). |
Example: 'usefmin',true
Data Types: boolean or struct
plots
—Plot on the screen.scalar.
If plots=1 the fan plot is produced else (default) no plot is produced.
REMARK: all the following options work only if plots=1
Example: 'plots',1
Data Types: double
conflev
—Confidence level.scalar | vector.
Confidence level for the bands (default is 0.99, that is we plot two horizontal lines in correspondence of value -2.58 and 2.58).
Example: 'conflev',[0.9 0.95 0.99]
Data Types: double
FontSize
—font size of the labels of the axes.scalar.
Default value is 12.
Example: 'FontSize',20
Data Types: double
labx
—a label for the x-axis.character.
default: 'Subset size m'
Example: 'labx','my labx'
Data Types: char
laby
—a label for the y-axis.character.
default:'Score test statistic'
Example: 'laby','my laby'
Data Types: char
lwd
—linewidth of the curves which
contain the score test.scalar.
Default line width=2.
Example: 'lwd',5
Data Types: double
lwdenv
—width of the lines associated
with the envelopes.scalar.
Default is lwdenv=1.
Example: 'lwdenv',5
Data Types: double
SizeAxesNum
—Scalar which controls the size of the numbers of the
axes.scalar.
Default value is 10.
Example: 'SizeAxesNum',12
Data Types: double
tag
—handle of the plot which is about to be created.character.
The default is to use tag 'pl_fan'. Notice that if the program finds a plot which has a tag equal to the one specified by the user, then the output of the new plot overwrites the existing one in the same window else a new window is created
Example:
'tag','mytag'
Data Types: char
titl
—a label for the title.character.
default: 'Fan plot'
Example: 'titl','my title'
Data Types: char
xlimx
—Minimum and maximum of the x axis.vector.
Default value is [init n]
Example: 'xlimx',[0 1]
Data Types: double
ylimy
—Minimum and maximum of the y axis.vector.
Default value for ylimy(1)=max(min(score_test),-20).
Default value for ylimy(2)=min(max(score_test),20).
Example: 'ylimy',[0 1]
Data Types: double
Output Arguments
out — description
Structure
Structure which contains the following fields
| Value | Description |
|---|---|
Score |
(n-init+1) x length(la)+1 matrix containing the values of the score test for each value of the transformation parameter: 1st col = fwd search index; 2nd col = value of the score test in each step of the fwd search for la(1); ........... end col = value of the score test in each step of the fwd search for la(end). |
Scorep |
(n-init+1) x length(la)+1 matrix containing the values of the score test for positive observations for each value of the transformation parameter. 1st col = fwd search index; 2nd col = value of the (positive) score test in each step of the fwd search for la(1); ........... end col = value of the (positive) score test in each step of the fwd search for la(end). Note that this output is present only if input option family is 'YJpn' or 'YJall'. |
Scoren |
(n-init+1) x length(la)+1 matrix containing the values of the score test for positive observations for each value of the transformation parameter: 1st col = fwd search index; 2nd col = value of the (negative) score test in each step of the fwd search for la(1); ........... end col = value of the (negative) score test in each step of the fwd search for la(end). Note that this output is present only if input option family is 'YJpn' or 'YJall'. |
Scoreb |
(n-init+1) x length(la)+1 matrix containing the values of the score test for the joint presence of both constructed variables (associated with positive and negative observations) for each value of the transformation parameter. In this case the reference distribution is the F with 2 and subset_size-p degrees of freedom. 1st col = fwd search index (subset_size); 2nd col = value of the score test in each step of the fwd search for la(1); ........... end col = value of the score test in each step of the fwd search for la(end). Note that this output is present only if input option family is 'YJall' |
Scoremle |
(n-init+1) x length(la)+1 matrix containing the values of the (score) likelihood ratio test for the joint presence of both constructed variables (associated with positive and negative observations) for each value of the transformation parameter. In this case the reference distribution is the F with 2 and subset_size-p degrees of freedom. 1st col = fwd search index (subset_size); 2nd col = value of the score test in each step of the fwd search for la(1); ........... end col = value of the score test in each step of the fwd search for la(end). Note that this output is present only if input option scoremle is true |
ScoreT |
(n-init+1) x length(la)+1 matrix containing the values of the Tukey's one degree of freedome test for non-additivity for each value of the transformation parameter. 1st col = fwd search index; 2nd col = value of the Tukey's test in each step of the fwd search for la(1); ........... end col = value of the Tukey's test in each step of the fwd search for la(end). Note that this output is present only if input option tukey1df is true. |
laMLE |
(n-init+1) x 2*length(la)+1 matrix containing the values of the maximum likelihood estimate of laP and laN. Columns 2:3 are associated with the search which has ordered the data using to la(1); ......... Columns 2*length(la):2*length(la)+1 are associated with the search which has ordered the data using to la(length(la)). Note that out.laMLE(end,2)=out.laMLE(end,2)=...=out.laMLE(end,2*length(la)) because all these variables contain the MLE of laP based on all the observations. Similarly notice that out.laMLE(end,3)=out.laMLE(end,5)=...=out.laMLE(end,2*length(la)+1) because all these variables contain the MLE of laN based on all the observations. This output is present only if input option scoremle is true. |
la |
vector containing the values of lambda for which fan plot is constructed |
bs |
matrix of size p x length(la) containing the units forming the initial subset for each value of lambda |
Un |
cell of size length(la). out.Un{i} is a n-init) x 11 matrix which contains the unit(s) included in the subset at each step in the search associated with la(i). REMARK: in every step the new subset is compared with the old subset. Un contains the unit(s) present in the new subset but not in the old one. Un(1,:), for example, contains the unit included in step init+1 ... ; Un(end,2) contains the units included in the final step of the search |
class |
'FSRfan'. |
y |
A vector with n elements that contains the response variable which has been used |
X |
Data matrix of explanatory variables which has been used (it also contains the column of ones if input option intercept was missing or equal to 1) |
References
Atkinson, A.C. and Riani, M. (2000), "Robust Diagnostic Regression Analysis", Springer Verlag, New York.
Atkinson, A.C. and Riani, M. (2002a), Tests in the fan plot for robust, diagnostic transformations in regression, "Chemometrics and Intelligent Laboratory Systems", Vol. 60, pp. 87-100.
Atkinson, A.C. Riani, M., Corbellini A. (2019), The analysis of transformations for profit-and-loss data, Journal of the Royal Statistical Society, Series C, "Applied Statistics", https://doi.org/10.1111/rssc.12389
Atkinson, A.C. Riani, M. and Corbellini A. (2021), The Box–Cox Transformation: Review and Extensions, "Statistical Science", Vol. 36, pp. 239-255, https://doi.org/10.1214/20-STS778

|
FSRenvmdr |
FSRH |
 |
|
|
Functions |
|
• The developers of the toolbox • The forward search group • Terms of Use • Acknowledgments