fanBICpn
fanBICpn uses the output of FSRfan called with input option family 'YJpn' to choose la_P and la_N
Description
Examples
 Example of use of FSRfanBICpn with all default options.
Example of use of FSRfanBICpn with all default options.
 Example of use of FSRfanBICpn with all default options.
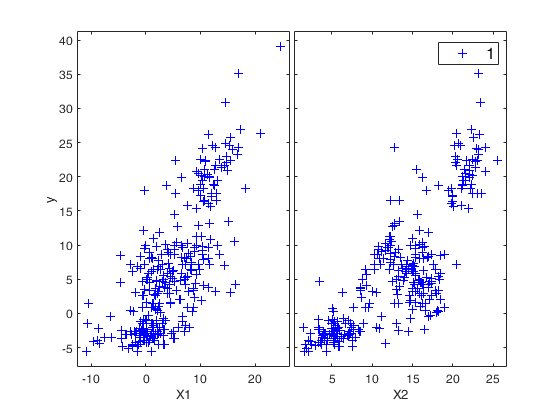
Example of use of FSRfanBICpn with all default options.Load the Investment funds data.
YY=load('fondi_large.txt');
y=YY(:,2);
X=YY(:,[1 3]);
yXplot(y,X);
n=length(y);
[outFSRfan]=FSRfan(y,X,'plots',0,'init',round(n*0.3),'nsamp',10000,'la',[0 0.25 0.5 0.75 1 1.25],'msg',0,'family','YJ');
[outini]=fanBIC(outFSRfan,'plots',0);
% labest is the best value imposing the constraint that positive and
% negative observations must have the same transformation parameter.
labest=outini.labest;
% Compute test for positive and test for negative using labest
[outFSRfanpn]=FSRfan(y,X,'msg',0,'family','YJpn','la',labest,'plots',0);
% Check if two different transformations are needed for positive and negative values
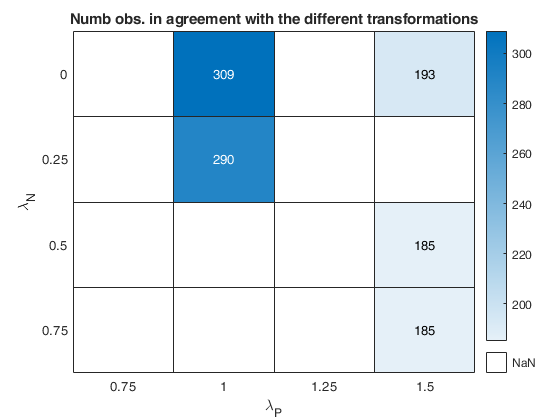
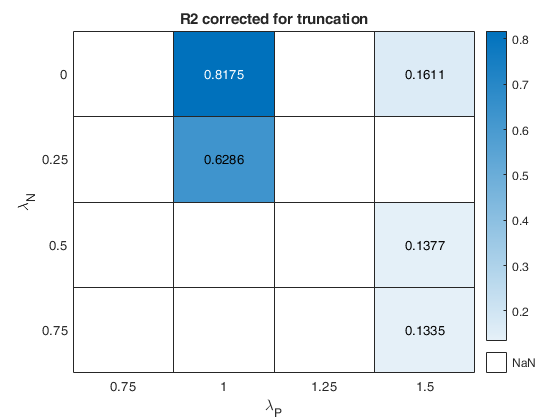
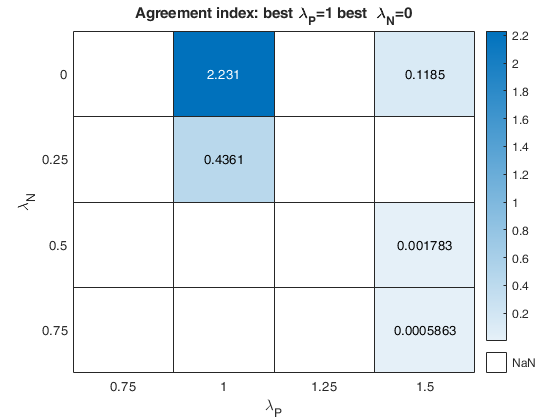
out=fanBICpn(outFSRfanpn);
Analyzing la_P=0.75 and la_N=0.25 Analyzing la_P=0.75 and la_N=0 Analyzing la_P=0.75 and la_N=0.75 Analyzing la_P=0.75 and la_N=0.5 Analyzing la_P=1 and la_N=0.25 Analyzing la_P=1 and la_N=0 Analyzing la_P=1 and la_N=0.75 Analyzing la_P=1 and la_N=0.5 Analyzing la_P=1.25 and la_N=0.25 Analyzing la_P=1.25 and la_N=0 Analyzing la_P=1.25 and la_N=0.75 Analyzing la_P=1.25 and la_N=0.5 Analyzing la_P=1.5 and la_N=0.25 Analyzing la_P=1.5 and la_N=0 Analyzing la_P=1.5 and la_N=0.75 Analyzing la_P=1.5 and la_N=0.5
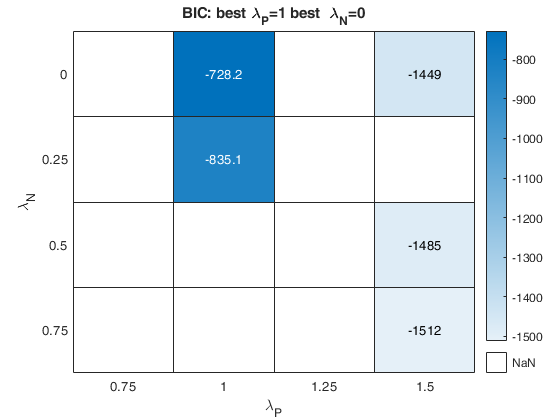
 Example of the use of option laRangeAndStep.
Example of the use of option laRangeAndStep.
 Example of the use of option laRangeAndStep.
Example of the use of option laRangeAndStep.Use simulated data from Atkinson Riani and Corbellini (2020)
rng('default')
rng(10)
n=1000;
p=3;
kk=200;
X=randn(n,p);
beta=[ 1; 1; 1]*0.3;
sig=0.5;
eta=X*beta;
init=6;
lapos=1.5;
laneg=0;
y=eta+sig*randn(n,1);
% Data contamination
y(1:kk)=y(1:kk)-1.9;
ypos=y>0;
ytra=y;
ytra(ypos)=normYJ(y(ypos),[],lapos,'inverse',true,'Jacobian',false);
ytra(~ypos)=normYJ(y(~ypos),[],laneg,'inverse',true,'Jacobian',false);
y=ytra;
% Initial fan plot
outFSRfan=FSRfan(y,X,'la',[0.5 0.75 1 1.25 1.5],'family','YJ','plots',0,'init',init,'msg',0);
% Find best value of lambda according to BIC
% (same value of lambda for positive and negative observations).
[outUniqueLambda]=fanBIC(outFSRfan,'plots',0);
BIC=outUniqueLambda.BIC;
labest=outUniqueLambda.labest;
% Check if two different transformations are needed for positive and negative values
[outFSRfanpn]=FSRfan(y,X,'msg',0,'family','YJpn','la',labest);
% option laRangeAndStep
laRangeAndStep=[1.5 0.25 0.5];
out=fanBICpn(outFSRfanpn,'laRangeAndStep',laRangeAndStep);
Analyzing la_P=1.5 and la_N=0.5 Analyzing la_P=1.5 and la_N=0 Analyzing la_P=1.5 and la_N=1.5 Analyzing la_P=1.5 and la_N=1 Analyzing la_P=1.5 and la_N=0.25 Analyzing la_P=1.5 and la_N=1.25 Analyzing la_P=1.5 and la_N=0.75 Analyzing la_P=1.75 and la_N=0.5 Analyzing la_P=1.75 and la_N=0 Analyzing la_P=1.75 and la_N=1.5 Analyzing la_P=1.75 and la_N=1 Analyzing la_P=1.75 and la_N=0.25 Analyzing la_P=1.75 and la_N=1.25 Analyzing la_P=1.75 and la_N=0.75 Analyzing la_P=2 and la_N=0.5 Analyzing la_P=2 and la_N=0 Analyzing la_P=2 and la_N=1.5 Analyzing la_P=2 and la_N=1 Analyzing la_P=2 and la_N=0.25 Analyzing la_P=2 and la_N=1.25 Analyzing la_P=2 and la_N=0.75
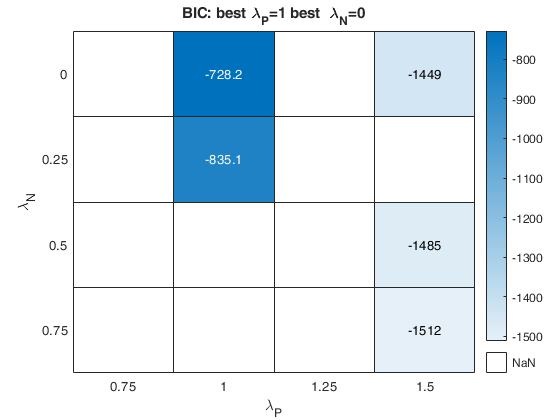
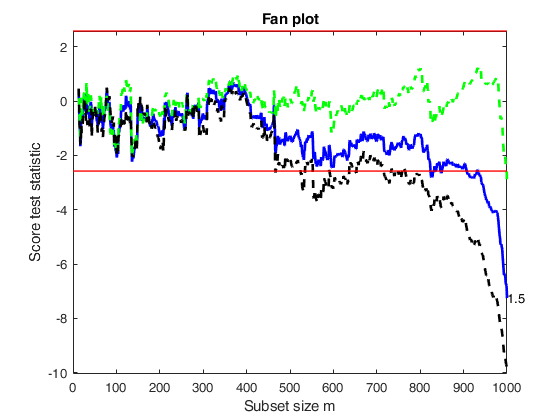
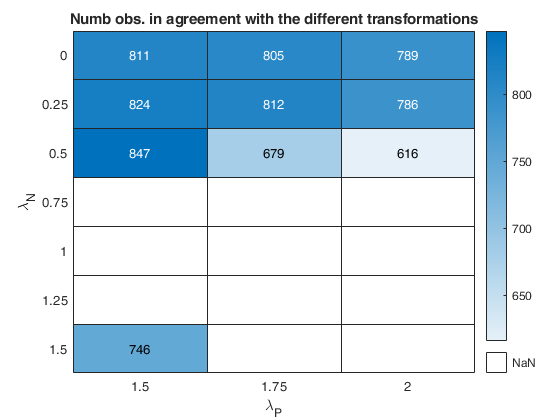
Related Examples
 Example of the use of options fraciniFSR and plots.
Example of the use of options fraciniFSR and plots.
 Example of the use of options fraciniFSR and plots.
Example of the use of options fraciniFSR and plots.Balance sheets data.
XX=load('BalanceSheets.txt');
% Define X and y
y=XX(:,6);
X=XX(:,1:5);
n=length(y);
la=[0 0.25 0.5 0.75 1 1.25];
[outFSRfan]=FSRfan(y,X,'plots',1,'init',round(n*0.3),'nsamp',5000,'la',la,'msg',0,'family','YJ');
[outini]=fanBIC(outFSRfan,'plots',0);
% labest is the best value imposing the constraint that positive and
% negative observations must have the same transformation parameter.
labest=outini.labest;
% Compute test for positive and test for negative using labest
indexlabest=find(labest==la);
% Find initial subset to initialize the search.
lms=outFSRfan.bs(:,indexlabest);
[outFSRfanpn]=FSRfan(y,X,'msg',0,'family','YJpn','la',labest,'plots',0,'lms',lms);
% Check if two different transformations are needed for positive and negative values
% Start monitoring the exceedances in the subset in agreement with a
% transformation from 90 per cent.
fraciniFSR=0.90;
% option plots (just show the BIC and the agreement index plot).
plots=struct;
plots.name={'BIC','AGI'};
nsamp=2000;
out=fanBICpn(outFSRfanpn,'fraciniFSR',fraciniFSR,'plots',plots,'nsamp',nsamp);
Analyzing la_P=0 and la_N=1 Analyzing la_P=0 and la_N=0.75 Analyzing la_P=0 and la_N=1.5 Analyzing la_P=0 and la_N=1.25 Analyzing la_P=0.25 and la_N=1 Analyzing la_P=0.25 and la_N=0.75 Analyzing la_P=0.25 and la_N=1.5 Analyzing la_P=0.25 and la_N=1.25 Analyzing la_P=0.5 and la_N=1 Analyzing la_P=0.5 and la_N=0.75 Analyzing la_P=0.5 and la_N=1.5 Analyzing la_P=0.5 and la_N=1.25 Analyzing la_P=0.75 and la_N=1 Analyzing la_P=0.75 and la_N=0.75 Analyzing la_P=0.75 and la_N=1.5 Analyzing la_P=0.75 and la_N=1.25
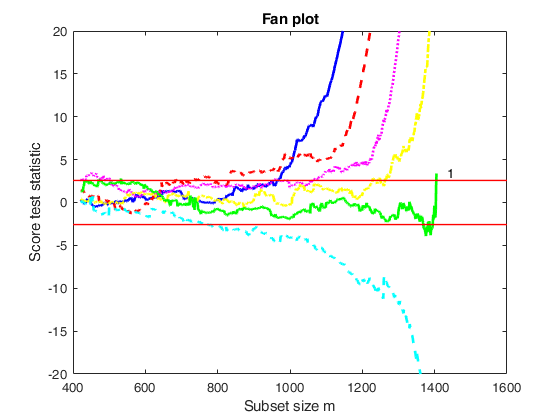
Input Arguments
outFSRfan — Structure created with function FSRfan.
Structure.
Structure containing the following fields
| Value | Description |
|---|---|
Score |
(n-init) x length(la)+1 matrix: 1st col = fwd search index; 2nd col = value of the score test in each step of the fwd search for la; |
Scorep |
(n-init) x 2 matrix containing the values of the score test for positive observations for each value of the transformation parameter. 1st col = fwd search index; 2nd col = value of the (positive) score test in each step of the fwd search for la; |
Scoren |
(n-init) x 2 matrix containing the values of the score test for positive observations for each value of the transformation parameter: 1st col = fwd search index; 2nd col = value of the (negative) score test in each step of the fwd search for la; |
Scoreb |
(n-init) x 2+1 matrix containing the values of the score test for the joint presence of both constructed variables (associated with positive and negative observations) for each value of the transformation parameter. In this case the reference distribution is the with 2 and subset_size-p degrees of freedom. 1st col = fwd search index (subset_size); 2nd col = value of the score test in each step of the fwd search for la; |
Scoremle |
(n-init) x 2 matrix containing the values of the (score) likelihood ratio test for the joint presence of both constructed variables (associated with positive and negative observations) for each value of the transformation parameter. In this case the reference distribution is the F with 2 and subset_size-p degrees of freedom. 1st col = fwd search index (subset_size); 2nd col = value of the score test in each step of the fwd search for la; outFSRfan.Scoremle is present only if FSRfan has been called with input option scoremle set to true. |
la |
scalar containing the value of lambda for which FSRfan was computed. |
bs |
matrix of size p x 1 containing the units forming the initial subset for lambda. |
y |
a vector containing the response |
X |
a matrix containing the explanatory variables. Note that this matrix includes the column of ones. |
Data Types: struct
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'laRangeAndStep',[1 0.2 1.2]
, 'conflev',[0.999]
, 'fraciniFSR',0.85
, 'init',100 starts monitoring from step m=100
, 'bonflev',0.99
, 'scoremle',true
, 'nsamp',1000
, 'msg',1
, 'plots', 1
laRangeAndStep
—values of laP and laN to explore.vector of length 3.
The grid search for laP and laN is done in the grid outFSRfan.la(1)-laRangeAndStep(1):laRangeAndStep(2):outFSRfan.la(1)+laRangeAndStep(3).
For example, If laRangeAndStep(1)=0.8, laRangeAndStep(2) is 0.1 and laRangeAndStep(3)=0.6 and input parameter outFSRfan.la(1)=0.5, the grid search for laP and laN is done in the grid (0.5-0.8):0.1:(0.5+0.6). The default value for laRangeAndStep is [0.75 0.25 0.75].
Example: 'laRangeAndStep',[1 0.2 1.2]
Data Types: double
conflev
—Confidence level.scalar.
Confidence level to evaluate the exceedances in the fanplot.
Default confidence level is 0.9999 that is signals are considered when there is an exceedance for confidence level for at least 3 consecutive times.
Example: 'conflev',[0.999]
Data Types: double
fraciniFSR
—fraction of observations to initialize search for outlier detection.scalar.
After exceedance procedure based on the score test a subset of observations in agreement with a transformation is found. On this subset we perform outlier detection using FSR. fraciniFSR specifies the fraction of observations to start monitoring exceedances of the minimum deletion residuals. The default value of fraciniFSR is 0.8.
Example: 'fraciniFSR',0.85
Data Types: double
init
—Step to start monitoring exceedances.scalar.
It specifies the initial subset size to start monitoring exceedances of the fanplot. If init is not specified it set equal to round(n*0.6):
Example: 'init',100 starts monitoring from step m=100
Data Types: double
bonflev
—Signal to use to identify outliers.scalar.
Option to be used if the distribution of the data is strongly non normal and, thus, the general signal detection rule based on consecutive exceedances cannot be used. In this case bonflev can be: - a scalar smaller than 1 which specifies the confidence level for a signal and a stopping rule based on the comparison of the minimum MD with a Bonferroni bound. For example if bonflev=0.99 the procedure stops when the trajectory exceeds for the first time the 99% bonferroni bound.
- A scalar value greater than 1. In this case the procedure stops when the residual trajectory exceeds for the first time this value.
Default value is '', which means to rely on general rules based on consecutive exceedances.
Example: 'bonflev',0.99
Data Types: double
scoremle
—likelihood ratio test for the two different transformation
parameters \lambda_P and \lambda_N.boolean.
If scoremle is true and field Scoremle is present in input structure outFSRfan is present we check exceedance of the threshold according to likelihood ratio test else we check exceedance of the threshold according to outFSRfan.Scoreb.
Example: 'scoremle',true
Data Types: logical
nsamp
—Number of subsamples to extract.scalar.
Number of subsamples which will be extracted in order to find initial subset for each candidate value of lambda.
If nsamp=0 all subsets will be extracted. They will be (n choose p). Remark: if the number of all possible subset is <1000 the default is to extract all subsets otherwise just 1000.
Example: 'nsamp',1000
Data Types: double
msg
—Level of output to display.scalar.
It controls whether to display or not messages on the screen If msg==1 (default) messages are displayed on the screen about values or la_P and la_N which are being analyzed.
else no message is displayed on the screen.
Example: 'msg',1
Data Types: double
plots
—Plot on the screen.scalar structure.
Case 1: plots option used as scalar.
- If plots=0, plots are not generated.
- If plots=1 (default), 4 heatmaps are shown on the screen.
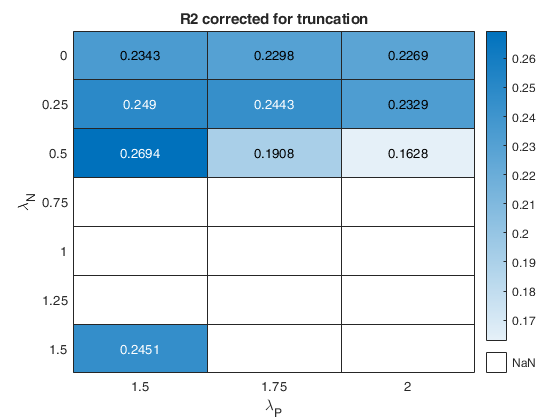
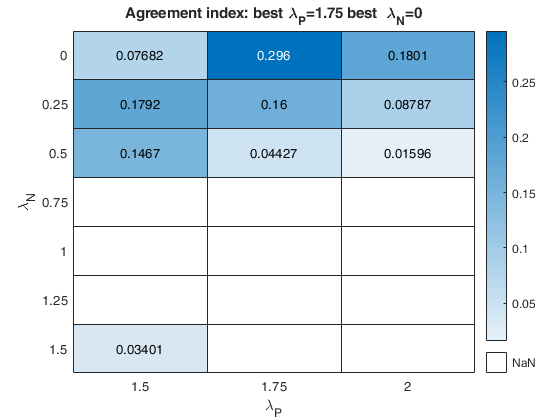
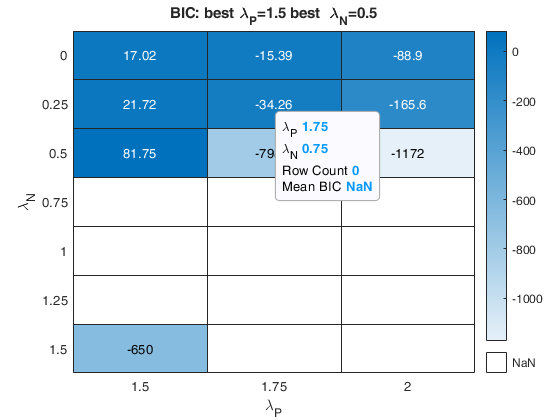
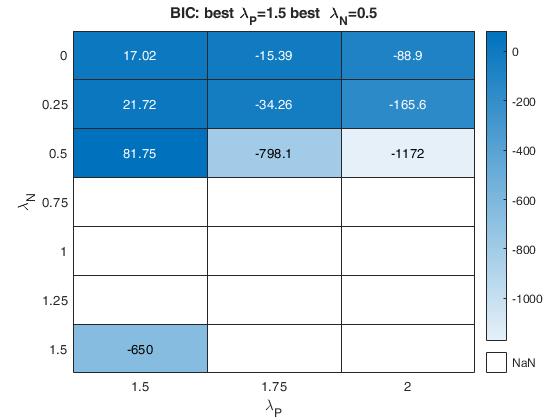
The first plot ("BIC") shows the values of BIC, the second ("AGI") shows the values of the agreement index, the third ('Obs') the number of observations in agreement with the transformation excluding the outliers and the fourth ('R2c') the final value of R2 (corrected for truncation).
Case 2: plots option used as struct.
If plots is a structure it may contain the following fields:
| Value | Description |
|---|---|
name |
cell array of strings which enables to specify which plot to display. plots.name={'Obs'; 'BIC'; 'AGI'; 'R2c'}; is exactly equivalent to plots=1 For the explanation of the above plots see plots=1. If plots.name=={ 'Obs'; 'BIC'; 'AGI'; 'R2c';... 'ObsWithOut'; 'AGIW'; 'R2'}; or plots.name={'all'}; it is also possible to view the heatmap referred to the number of observations in agreement with transformation before outlier detection ('ObsWithOut') the weighted version of the agreement index ('AGIW') and the original value of R2 before correction for truncation. |
Example: 'plots', 1
Data Types: single | double | struct
Output Arguments
out — description
Structure
Structure which contains the following fields
| Value | Description |
|---|---|
Summary |
k-by-9 table where k is the number of values of laPosxlaNeg which have been considered. out.Summary contains the following information: 1st column= value of laPos (transformation for positive values of y); 2nd column= value of laNeg (transformation for negative values of y); 3rd col = number of observations in agreement with the transformation before outlier detection; 4th col = number of observations in agreement with the transformation after outlier detection; 5th col = value of BIC; 6th col = value of the agreement index; 7th col = value of the agreement index weighted; 8th col = value of R2 based on observations in agreement with transformation after outlier detection. 9th col = value of R2 corrected for elliptical truncation. |
labestBIC |
vector of length 2 containing best values of laP and laN according to BIC. |
labestAGI |
vector of length 2 containing best values of laP and laN according to agreement index. |
ty |
transformed response according to out.labestBIC. |
rsq |
the multiple R-squared value for the transformed values |
y |
n x 1 vector containing the original y values. |
X |
n x p matrix containing the original X matrix. |
References
Atkinson, A.C. and Riani, M. (2000), "Robust Diagnostic Regression Analysis", Springer Verlag, New York.
Atkinson, A.C. and Riani, M. (2002a), Tests in the fan plot for robust, diagnostic transformations in regression, "Chemometrics and Intelligent Laboratory Systems", Vol. 60, pp. 87-100.
Atkinson, A.C. Riani, M., Corbellini A. (2019), The analysis of transformations for profit-and-loss data, Journal of the Royal Statistical Society, Series C, "Applied Statistics", https://doi.org/10.1111/rssc.12389
Atkinson, A.C. Riani, M. and Corbellini A. (2021), The Box–Cox Transformation: Review and Extensions, "Statistical Science", Vol. 36, pp. 239-255, https://doi.org/10.1214/20-STS778

|
fanBIC |
fanplot |
 |
|
|
Functions |
|
• The developers of the toolbox • The forward search group • Terms of Use • Acknowledgments