fanBIC

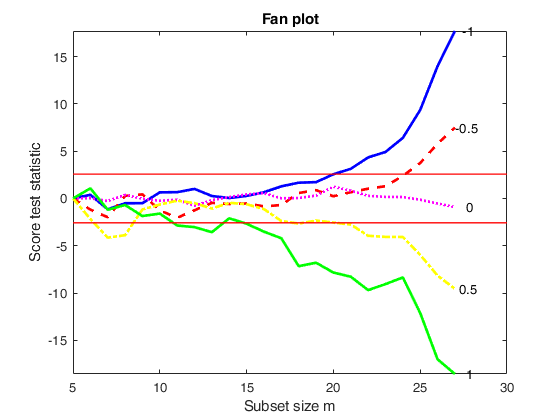
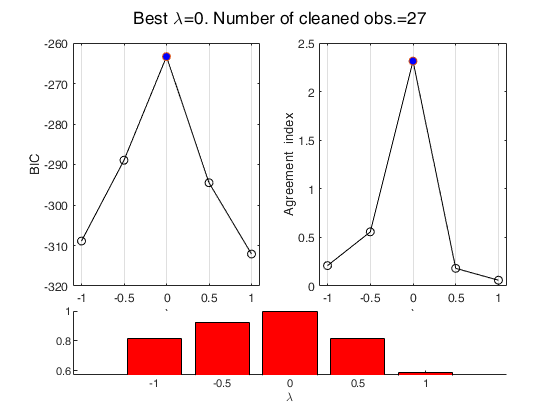
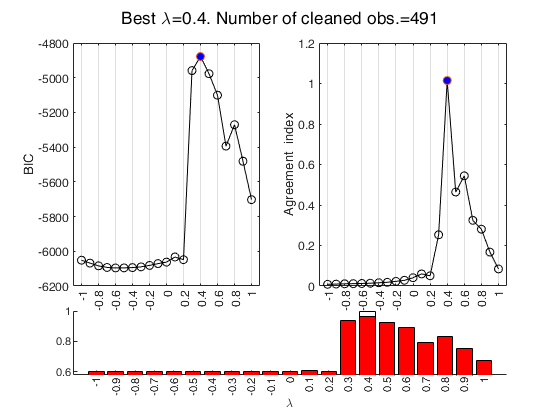
fanBIC uses the output of FSRfan to choose the best value of the transformation parameter in linear regression

expand all in page

Syntax

  • out=fanBIC(outFSRfan)example
  • out=fanBIC(outFSRfan,Name,Value)example

Description

example

out =fanBIC(outFSRfan) fanBIC with all default options.

example

out =fanBIC(outFSRfan, Name, Value) BIC plot with optional arguments.

Examples

expand all

  • fanBIC with all default options.

    • load the wool data. 

    XX=load('wool.txt');
y=XX(:,end);
X=XX(:,1:end-1);
% FSRfan and fanplot with all default options
[outFSR]=FSRfan(y,X,'msg',0);
out=fanBIC(outFSR);
    Click here for the graphical output of this example (link to Ro.S.A. website).

  • BIC plot with optional arguments.

    • FSRfan and fanBIC with specified lambda. 

    load('loyalty.txt');
y=loyalty(:,4);
X=loyalty(:,1:3);
% la = vector containing the grid of values to use for the
% transformation parameter
la=-1:0.1:1;
[outFSRfan]=FSRfan(y,X,'la',la,'msg',0,'plots',0);
out=fanBIC(outFSRfan);
    Click here for the graphical output of this example (link to Ro.S.A. website).

    Input Arguments

    expand all

    outFSRfan — Structure created with function FSRfan. Structure.

    Structure containing the following fields

    Value Description
    Score

    (n-init) x length(la)+1 matrix: 1st col = fwd search index;

    2nd col = value of the score test in each step of the fwd search for la(1);

    ...;

    last col = value of the score test in each step of the fwd search for la(end).
    la

    vector containing the values of lambda for which FSRfan was computed
    bs

    matrix of size p x length(la) containing the units forming the initial subset for each value of lambda.
    y

    a vector containing the response
    X

    a matrix containing the explanatory variables

    Data Types: struct

    Name-Value Pair Arguments

    Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

    Example: 'conflev',[0.999] , 'init',100 starts monitoring from step m=100 , 'family','YJ' , 'bonflev',0.99 , 'plots',1 , 'tag','pl_myfanBIC'

    conflev —Confidence level.scalar.

    Confidence level to evaluate the exceedances in hte fanplot.

    Default confidence level is 0.9999 that is signals are considered when there is an exceedance for confidence level for at least 3 consecutive times.

    Example: 'conflev',[0.999]

    Data Types: double

    init —Step to start monitoring exceedances.scalar.

    It specifies the initial subset size to start monitoring exceedances of the fanplot. If init is not specified it set equal to round(n*0.6).

    Example: 'init',100 starts monitoring from step m=100

    Data Types: double

    family —string which identifies the family of transformations which must be used.character.

    Possible values are 'BoxCox' (default), 'YJ', 'YJpn' or 'YJall'.

    The Box-Cox family of power transformations equals $(y^{\lambda}-1)/\lambda$ for $\lambda$ not equal to zero, and $\log(y)$ if $\lambda = 0$.

    The Yeo-Johnson (YJ) transformation is the Box-Cox transformation of $y+1$ for nonnegative values, and of $|y|+1$ with parameter $2-\lambda$ for $y$ negative.

    Remember that BoxCox can be used just if input y is positive. Yeo-Johnson family of transformations does not have this limitation.

    Example: 'family','YJ'

    Data Types: char

    bonflev —Signal to use to identify outliers.scalar.

    Option to be used if the distribution of the data is strongly non normal and, thus, the general signal detection rule based on consecutive exceedances cannot be used. In this case bonflev can be: - a scalar smaller than 1 which specifies the confidence level for a signal and a stopping rule based on the comparison of the minimum MD with a Bonferroni bound. For example if bonflev=0.99 the procedure stops when the trajectory exceeds for the first time the 99% bonferroni bound.

    - A scalar value greater than 1. In this case the procedure stops when the residual trajectory exceeds for the first time this value.

    Default value is '', which means to rely on general rules based on consecutive exceedances.

    Example: 'bonflev',0.99

    Data Types: double

    plots —Plot on the screen.scalar.

    If plots=1 a three panel plot will be produced. The left panel contains the BIC for the various values of lambda, the right panel the index of agreement with MLE, while the bottom panel the fraction of observations in agreement with the different values of lambda.

    Example: 'plots',1

    Data Types: double

    tag —Handle of the plot.string.

    String which identifies the handle of the plot which is about to be created. The default is to use tag pl_fanBIC. Notice that if the program finds a plot which has a tag equal to the one specified by the user, then the output of the new plot overwrites the existing one in the same window else a new window is created.

    Example: 'tag','pl_myfanBIC'

    Data Types: char

    Output Arguments

    expand all

    out — description Structure

    Structure which contains the following fields

    Value Description
    BIC

    length(la)-by-3 matrix containing in the first column the values of lambda, in the second column the values of BIC and in the third column the values of the "Agreement index". The agreement index is the reciprocal of the mean of the absolute values of the score test computed in the interval init:h. The default value of init is n*0.6 (see input option init) and h is the number of clean observations in agreement with a particular transformation. h is contained in the third column of out.mmstop. The value of the index is rescaled with the variance of the truncated normal distribution, in order to give more weight to the searches with larger values of h.
    mmstop

    length(la)-by-3 matrix containing in the first column the values of lambda, in the second column the number of units in agreement with the different values of lambda and in the third column the number of units not declared as outliers in the subsequent outlier detection procedure.
    BBla

    n-by-length(la) matrix containing information about the outlier(s) for each value of lambda.

    If out.BBla(i,j)=0 means that unit i (i=1, 2, ...n) is not in agrement with la(j) j=1, 2, ..., length(la).

    If out.BBla(i,j)=1 means that unit i (i=1, 2, ...n) is in agrement with la(j) j=1, 2, ..., length(la) but has been declared as outlier in the subsequent outlier detection procedure.

    If out.BBla(i,j)=2 means that unit i (i=1, 2, ...n) is in agrement with la(j) j=1, 2, ..., length(la) and has not been declared as outlier in the subsequent outlier detection procedure.
    labest

    scalar. Value of lambda associated with the largest BIC value.

    References

    Atkinson, A.C. and Riani, M. (2000), "Robust Diagnostic Regression Analysis", Springer Verlag, New York.

    Atkinson, A.C. and Riani, M. (2002a), Tests in the fan plot for robust, diagnostic transformations in regression, "Chemometrics and Intelligent Laboratory Systems", Vol. 60, pp. 87-100.

    Atkinson, A.C. Riani, M., Corbellini A. (2019), The analysis of transformations for profit-and-loss data, Journal of the Royal Statistical Society, Series C, "Applied Statistics", https://doi.org/10.1111/rssc.12389

    Atkinson, A.C. Riani, M. and Corbellini A. (2021), The Box–Cox Transformation: Review and Extensions, "Statistical Science", Vol. 36, pp. 239-255, https://doi.org/10.1214/20-STS778

    See Also

    |

    This page has been automatically generated by our routine publishFS