FSRfan

FSRfan monitors the values of the score test statistic for each lambda

expand all in page

Syntax

Description

The transformations for negative and positive responses were determined by Yeo and Johnson (2000) by imposing the smoothness condition that the second derivative of zYJ(λ) with respect to y be smooth at y = 0. However some authors, for example Weisberg (2005), query the physical interpretability of this constraint which is oftern violated in data analysis. Accordingly, Atkinson et al (2019) and (2020) extend the Yeo-Johnson transformation to allow two values of the transformations parameter: $\lambda_N$ for negative observations and $\lambda_P$ for non-negative ones.

FSRfan monitors: 1) the t test associated with the constructed variable computed assuming the same transformation parameter for positive and negative observations fixed. In short we call this test, "global score test for positive observations".

2) the t test associated with the constructed variable computed assuming a different transformation for positive observations keeping the value of the transformation parameter for negative observations fixed. In short we call this test, "test for positive observations".

3) the t test associated with the constructed variable computed assuming a different transformation for negative observations keeping the value of the transformation parameter for positive observations fixed. In short we call this test, "test for negative observations".

4) the F test for the joint presence of the two constructed variables described in points 2) and 3.

4) the F likelihood ratio test based on the MLE of $\lambda_P$ and $\lambda_N$. In this case the residual sum of squares of the null model bsaed on a single trasnformation parameter $\lambda$ is compared with the residual sum of squares of the model based on data transformed data using MLE of $\lambda_P$ and $\lambda_N$.

example

out =FSRfan(y, X) FSRfan with all default options.

example

out =FSRfan(y, X, Name, Value) FSRfan with optional arguments.

Examples

expand all

  • FSRfan with all default options.

    • Store values of the score test statistic for the five most common values of $\lambda$. 

    % Produce also a fan plot and display it on the screen.
% Common part to all examples: load wool dataset.
XX=load('wool.txt');
y=XX(:,end);
X=XX(:,1:end-1);
% Function FSRfan stores the score test statistic.
% In this case we use the five most common values of lambda are considered
[out]=FSRfan(y,X);
fanplotFS(out);
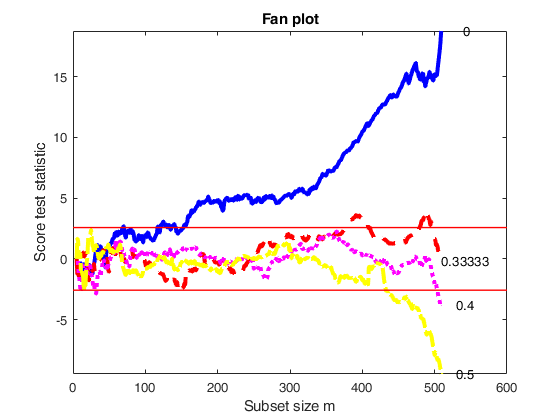
%The fan plot shows the log transformation is diffused throughout the data and does not depend on the presence of particular observations.
    Total estimated time to complete LMS:  0.00 seconds 
------------------------------
Warning: Number of subsets without full rank equal to 15.7%
Total estimated time to complete LMS:  0.00 seconds 
------------------------------
Warning: Number of subsets without full rank equal to 15.7%
Total estimated time to complete LMS:  0.00 seconds 
------------------------------
Warning: Number of subsets without full rank equal to 15.7%
Total estimated time to complete LMS:  0.00 seconds 
------------------------------
Warning: Number of subsets without full rank equal to 15.7%
Total estimated time to complete LMS:  0.00 seconds 
------------------------------
Warning: Number of subsets without full rank equal to 15.7%
    Click here for the graphical output of this example (link to Ro.S.A. website).

  • FSRfan with optional arguments.

    • Produce a personalized fan plot with required font sizes for labels and axes. 

    XX=load('wool.txt');
y=XX(:,end);
X=XX(:,1:end-1);
[out]=FSRfan(y,X,'plots',1,'FontSize',16,'SizeAxesNum',16);

    Related Examples

    expand all

  • Example specifying $\lambda$.

    • Produce a fan plot for each value of $\lambda$ inside vector la. 

    % Extract in matrix Un the units which entered the search in each step
XX=load('wool.txt');
y=XX(:,end);
X=XX(:,1:end-1);
la=[-1 -0.5 0 0.5];
[out]=FSRfan(y,X,'la',la,'plots',1);
Unsel=cell2mat(out.Un);
lla=length(la);
nr=size(Unsel,1)/lla;
Un=[Unsel(1:nr,1) reshape(Unsel(:,2),nr,lla)];

  • Example specifying the confidence level and the initial starting point for monitoring.

    • % Construct fan plot specifying the confidence level and the initial
% starting point for monitoring.
XX=load('wool.txt');
y=XX(:,end);
X=XX(:,1:end-1);
[out]=FSRfan(y,X,'init',size(X,2)+2,'nsamp',0,'conflev',0.95,'plots',1);

  • Example with starting point based on LTS.

    • Extraction of all subsamples, construct fan plot specifying the confidence level and the initial starting point for monitoring based on p+2 observations strong line width for lines associated with the confidence bands. 

    XX=load('wool.txt');
y=XX(:,end);
X=XX(:,1:end-1);
[out]=FSRfan(y,X,'init',size(X,2)+2,'nsamp',0,'lms',0,'lwdenv',3,'plots',1);

  • Fan plot using fidelity cards data.

    • In the example, la is the vector contanining the most common values of the transformation parameter. 

    % Store the score test statistics for the specified values of lambda
% and automatically produce the fan plot
XX=load('loyalty.txt');
namey='Sales'
y=XX(:,end);
nameX={'Number of visits', 'Age', 'Number of persons in the family'};
X=XX(:,1:end-1);
% la = vector contanining the most common values of the transformation
% parameter
la=[0 1/3 0.4 0.5];
% Store the score test statistics for the specified values of lambda
% and automatically produce the fan plot
[out]=FSRfan(y,X,'la',la,'init',size(X,2)+2,'plots',1,'lwd',3);
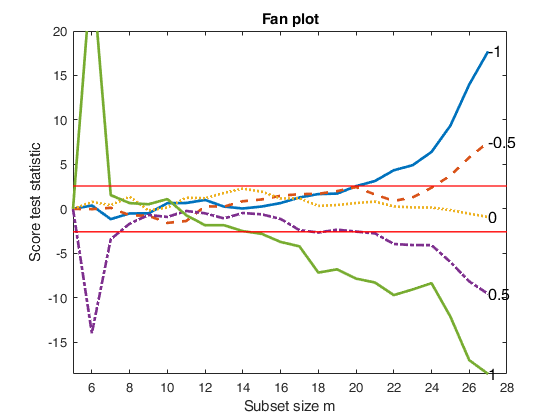
% The fan plot shows the even if the third root is the best value of the
% transformation parameter at the end of the search in earlier steps it
% lies very close to the upper rejection region. The best value of the
% transformation parameter seems to be the one associated with l=0.4
% which is always the confidence bands but at the end of search, due to
% the presence of particular observations it goes below the lower
% rejection line.
    namey =

    'Sales'

Total estimated time to complete LMS:  0.01 seconds 
Total estimated time to complete LMS:  0.01 seconds 
Total estimated time to complete LMS:  0.01 seconds 
Total estimated time to complete LMS:  0.01 seconds
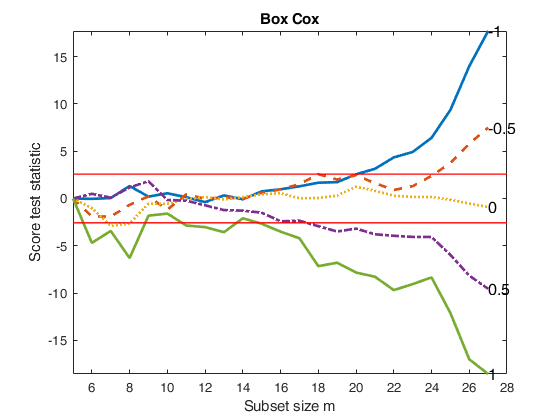
    Click here for the graphical output of this example (link to Ro.S.A. website)

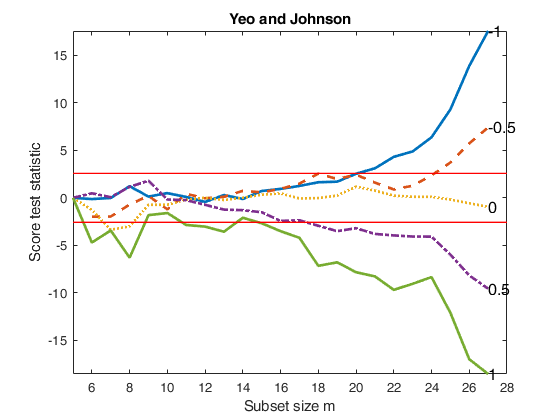
  • Compare BoxCox with Yeo and Johnson transformation.

    • Store values of the score test statistic for the five most common values of $\lambda$. 

    % Produce also a fan plot and display it on the screen.
% Common part to all examples: load wool dataset.
XX=load('wool.txt');
y=XX(:,end);
X=XX(:,1:end-1);
% Store the score test statistic using Box Cox transformation.
[outBC]=FSRfan(y,X,'nsamp',0);
% Store the score test statistic using Yeo and Johnson transformation.
[outYJ]=FSRfan(y,X,'family','YJ','nsamp',0);
fanplotFS(outBC,'titl','Box Cox');
fanplotFS(outYJ,'titl','Yeo and Johnson','tag','YJ');
disp('Maximum difference in absolute value')
disp(max(max(abs(outYJ.Score-outBC.Score))))
    Total estimated time to complete LMS:  0.04 seconds 
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
Total estimated time to complete LMS:  0.04 seconds 
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
Total estimated time to complete LMS:  0.04 seconds 
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
Total estimated time to complete LMS:  0.04 seconds 
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
Total estimated time to complete LMS:  0.05 seconds 
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
Total estimated time to complete LMS:  0.04 seconds 
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
Total estimated time to complete LMS:  0.04 seconds 
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
Total estimated time to complete LMS:  0.04 seconds 
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
Total estimated time to complete LMS:  0.04 seconds 
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
Total estimated time to complete LMS:  0.04 seconds 
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
Maximum difference in absolute value
    0.7564
    Click here for the graphical output of this example (link to Ro.S.A. website)

  • Example of monitoring of score test for positive and negative obseravations.

    • rng('default')
rng(10)
close all
n=200;
X=randn(n,3);
beta=[ 1; 1; 1];
sig=0.5;
y=X*beta+sig*randn(n,1);
disp('Fit in the true scale')
disp('R2 of the model in the true scale')
if verLessThanFS('8.1')
out=regstats(y,X,'linear',{'rsquare'});
disp(out.rsquare)
else
outlmori=fitlm(X,y);
disp(outlmori.Rsquared.Ordinary)
end
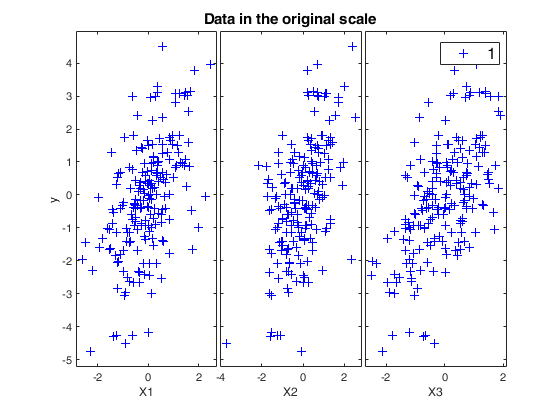
[~,~,BigAx]=yXplot(y,X,'tag','ori');
title(BigAx,'Data in the original scale')
% Find the data to transform
la=-0.25;
ytra=normYJ(y,[],la,'inverse',true);
if any(isnan(ytra))
disp('response with missing values')
end
disp('Fit in the transformed scale')
disp('R2 of the model in the wrong (inverse) scale')
if verLessThanFS('8.1')
out=regstats(ytra,X,'linear',{'rsquare'});
disp(out.rsquare)
else
outlmtra=fitlm(X,ytra);
disp(outlmtra.Rsquared.Ordinary)
end
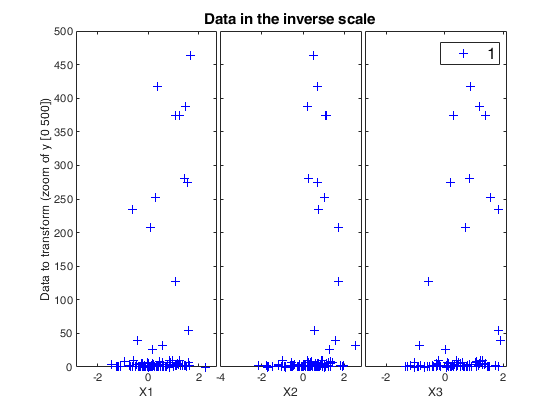
[~,~,BigAx]=yXplot(ytra,X,'tag','tra','namey','Data to transform (zoom of y [0 500])','ylimy',[0 500]);
title(BigAx,'Data in the inverse scale')
la=[ -0.5 -0.25 0];
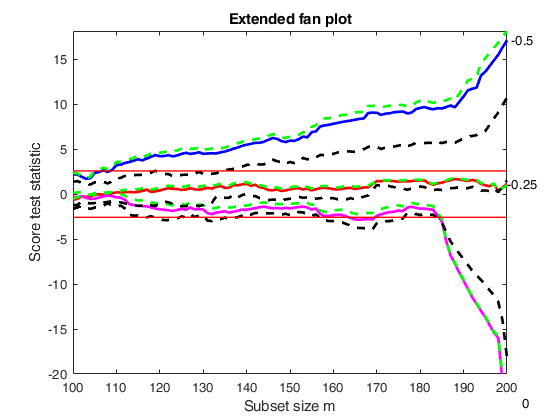
out=FSRfan(ytra,X,'la',la,'family','YJpn','plots',1,'init',round(n/2),'msg',0);
title('Extended fan plot')
    Fit in the true scale
R2 of the model in the true scale
    0.8993

Fit in the transformed scale
R2 of the model in the wrong (inverse) scale
    0.0471
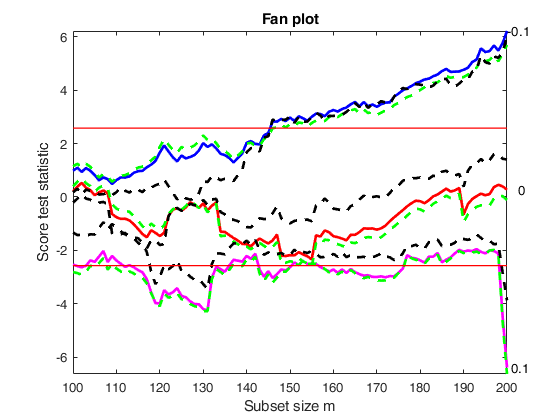
    Click here for the graphical output of this example (link to Ro.S.A. website)

  • Example of monitoring all score tests (also the F test).

    • rng('default')
rng(1000)
close all
n=200;
X=randn(n,3);
beta=[ 1; 1; 1];
sig=0.5;
y=X*beta+sig*randn(n,1);
% Find the data to transform
la=0;
ytra=normYJ(y,[],la,'inverse',true);
if any(isnan(ytra))
disp('response with missing values')
end
la=[ -0.1 0 0.1];
% In this case  family is YJall
out=FSRfan(ytra,X,'la',la,'family','YJall','plots',1,'init',round(n/2),'msg',0);
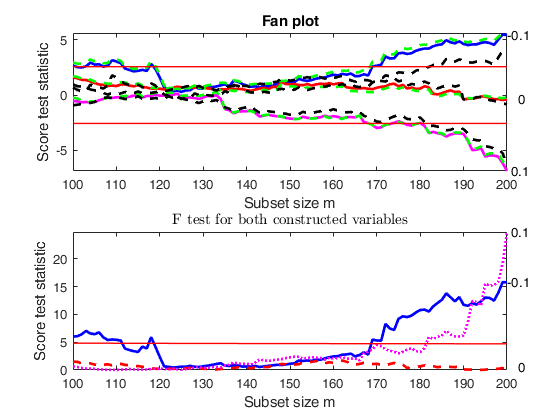
    Click here for the graphical output of this example (link to Ro.S.A. website)

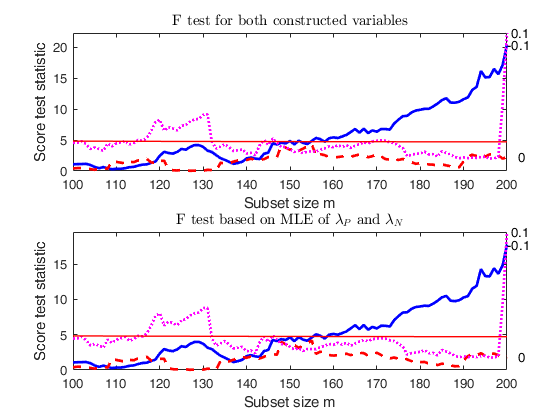
  • Comparison of F test based on constructed variables with F test based on MLE.

    • rng('default')
rng(100)
close all
n=200;
X=randn(n,3);
beta=[ 1; 1; 1];
sig=0.5;
y=X*beta+sig*randn(n,1);
% Find the data to transform
la=0;
ytra=normYJ(y,[],la,'inverse',true);
if any(isnan(ytra))
disp('response with missing values')
end
la=[ -0.1 0 0.1];
% Monitor test based on MLE using option scoremle
scoremle= true;
out=FSRfan(ytra,X,'la',la,'family','YJall','plots',1,'init',round(n/2),'msg',false,'scoremle',true);
    Click here for the graphical output of this example (link to Ro.S.A. website)

    Input Arguments

    expand all

    y — Response variable. Vector.

    A vector with n elements that contains the response variable. It can be either a row or a column vector.

    Data Types: single| double

    X — Predictor variables. Matrix.

    Data matrix of explanatory variables (also called 'regressors') of dimension (n x p-1). Rows of X represent observations, and columns represent variables. Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations. NOTICE THAT THE INTERCEPT MUST ALWAYS BE INCLUDED.

    Data Types: single| double

    Name-Value Pair Arguments

    Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

    Example: 'family','YJ' , 'h',5 , 'init',100 starts monitoring from step m=100 , 'intercept',false , 'la',[-1 -0.5] , 'lms',1 , 'msg',false , 'nocheck',true , 'nsamp',1000 , 'scoremle',true , 'usefmin',true , 'plots',1 , 'conflev',[0.9 0.95 0.99] , 'FontSize',20 , 'labx','my labx' , 'laby','my laby' , 'lwd',5 , 'lwdenv',5 , 'SizeAxesNum',12 , 'titl','my title' , 'xlimx',[0 1] , 'ylimy',[0 1]

    family —string which identifies the family of transformations which must be used.character.

    Possible values are 'BoxCox' (default), 'YJ', 'YJpn' or 'YJall'.

    The Box-Cox family of power transformations equals $(y^{\lambda}-1)/\lambda$ for $\lambda$ not equal to zero, and $\log(y)$ if $\lambda = 0$.

    The Yeo-Johnson (YJ) transformation is the Box-Cox transformation of $y+1$ for nonnegative values, and of $|y|+1$ with parameter $2-\lambda$ for $y$ negative.

    Remember that BoxCox can be used just if input y is positive. Yeo-Johnson family of transformations does not have this limitation.

    If family is 'YJpn' Yeo-Johnson family is applied but in this case it is also possible to monitor (in the output arguments out.Scorep and out.Scoren) the score test respectively for positive and negative observations.

    If family is 'YJall', it is also possible to monitor the joint F test for the presence of the two constructed variables for positive and negative observations.

    Example: 'family','YJ'

    Data Types: char

    h —The number of observations that have determined the least trimmed (median of) squares estimator.integer.

    Generally h is an integer greater or equal than [(n+size(X,2)+1)/2] but smaller then n

    Example: 'h',5

    Data Types: double

    init —Search initialization.scalar.

    It specifies the initial subset size to start monitoring the value of the score test, if init is not specified it will be set equal to: p+1, if the sample size is smaller than 40;

    min(3*p+1,floor(0.5*(n+p+1))), otherwise.

    Example: 'init',100 starts monitoring from step m=100

    Data Types: double

    intercept —Indicator for constant term.true (default) | false.

    Indicator for the constant term (intercept) in the fit, specified as the comma-separated pair consisting of 'Intercept' and either true to include or false to remove the constant term from the model.

    Example: 'intercept',false

    Data Types: boolean

    la —values of the transformation parameter for which it is necessary to compute the score test.vector.

    Default value of lambda is la=[-1 -0.5 0 0.5 1]; that is the five most common values of lambda

    Example: 'la',[-1 -0.5]

    Data Types: double

    lms —Criterion to use to find the initlal subset to initialize the search.scalar | Vector.

    If lms=1 (default) Least Median of Squares is computed, else Least trimmed of Squares is computed.

    If, lms is matrix with size p-1+intercept-by-length(la) it contains in column j=1,..., length(la) the list of units forming the initial subset for the search associated with la(j). In this last case previous input option nsamp is ignored.

    Example: 'lms',1

    Data Types: double

    msg —Level of output to display.boolean.

    Boolean scalar which controls whether to display or not messages on the screen.

    If msg==true (default) messages are displayed on the screen about estimated time to compute the LMS (LTS) for each value of lambda else no message is displayed on the screen

    Example: 'msg',false

    Data Types: logical

    nocheck —Check input arguments.boolean.

    If nocheck is equal to true no check is performed on matrix y and matrix X. Notice that y and X are left unchanged. In other words the additional column of ones for the intercept is not added. As default nocheck=false.

    Example: 'nocheck',true

    Data Types: boolean

    nsamp —Number of subsamples which will be extracted to find the robust estimator.scalar.

    If nsamp=0 all subsets will be extracted. They will be (n choose p). Remark: if the number of all possible subset is <1000 the default is to extract all subsets otherwise just 1000. If nsamp is a matrix of size r-by-p, it contains in the rows the subsets which sill have to be extracted. For example, if p=3 and nsamp=[ 2 4 9; 23 45 49; 90 34 1]; the first subset is made up of units [2 4 9], the second subset of units [23 45 49] and the third subset of units [90 34 1];

    Example: 'nsamp',1000

    Data Types: double

    scoremle —likelihood ratio test for the two different transformation parameters $\lambda_P$ and $\lambda_N$.boolean.

    If scoremle is true it is possible to compute the likelihood ratio test. In this case the residual sum of squares of the null model bsaed on a single trasnformation parameter $\lambda$ is compared with the residual sum of squares of the model based on data transformed data using MLE of $\lambda_P$ and $\lambda_N$. If scoremle is true it is possible through following option usefmin, to control the parameters of the optmization routine.

    Example: 'scoremle',true

    Data Types: logical

    usefmin —use solver to find MLE of lambda.boolean | struct.

    This option takes effect only when input option 'family' is 'YJpn' or 'YJall'. If usefmin is true or usefmin is a struct it is possible to use MATLAB solvers fminsearch or fminunc to find the maximum likelihood estimates of $\lambda_P$ and $\lambda_N$. The default value of usefmin is false that is solver is not used and the likelihood is evaluated at the grid of points with steps 0.01.

    If usefmin is a structure it may contain the following fields:

    Value Description
    MaxIter

    Maximum number of iterations (default is 1000).
    TolX

    Termination tolerance for the parameters (default is 1e-7).
    solver

    name of the solver. Possible values are 'fminsearch' (default) and 'fminunc'. fminunc needs the optimization toolbox.
    displayLevel

    amount of information displayed by the algorithm. possible values are 'off' (displays no information, this is the default), 'final' (displays just the final output) and 'iter' (displays iterative output to the command window).

    Example: 'usefmin',true

    Data Types: boolean or struct

    plots —Plot on the screen.scalar.

    If plots=1 the fan plot is produced else (default) no plot is produced.

    REMARK: all the following options work only if plots=1

    Example: 'plots',1

    Data Types: double

    conflev —Confidence level.scalar | vector.

    Confidence level for the bands (default is 0.99, that is we plot two horizontal lines in correspondence of value -2.58 and 2.58).

    Example: 'conflev',[0.9 0.95 0.99]

    Data Types: double

    FontSize —font size of the labels of the axes.scalar.

    Default value is 12.

    Example: 'FontSize',20

    Data Types: double

    labx —a label for the x-axis.character.

    default: 'Subset size m'

    Example: 'labx','my labx'

    Data Types: char

    laby —a label for the y-axis.character.

    default:'Score test statistic'

    Example: 'laby','my laby'

    Data Types: char

    lwd —linewidth of the curves which contain the score test.scalar.

    Default line width=2.

    Example: 'lwd',5

    Data Types: double

    lwdenv —width of the lines associated with the envelopes.scalar.

    Default is lwdenv=1.

    Example: 'lwdenv',5

    Data Types: double

    SizeAxesNum —Scalar which controls the size of the numbers of the axes.scalar.

    Default value is 10.

    Example: 'SizeAxesNum',12

    Data Types: double

    tag —handle of the plot which is about to be created.character.

    The default is to use tag 'pl_fan'. Notice that if the program finds a plot which has a tag equal to the one specified by the user, then the output of the new plot overwrites the existing one in the same window else a new window is created

    Example: 'tag','mytag'

    Data Types: char

    titl —a label for the title.character.

    default: 'Fan plot'

    Example: 'titl','my title'

    Data Types: char

    xlimx —Minimum and maximum of the x axis.vector.

    Default value is [init n]

    Example: 'xlimx',[0 1]

    Data Types: double

    ylimy —Minimum and maximum of the y axis.vector.

    Default value for ylimy(1)=max(min(score_test),-20).

    Default value for ylimy(2)=min(max(score_test),20).

    Example: 'ylimy',[0 1]

    Data Types: double

    Output Arguments

    expand all

    out — description Structure

    Structure which contains the following fields

    Value Description
    Score

    (n-init+1) x length(la)+1 matrix containing the values of the score test for each value of the transformation parameter: 1st col = fwd search index;

    2nd col = value of the score test in each step of the fwd search for la(1);

    ...........

    end col = value of the score test in each step of the fwd search for la(end).
    Scorep

    (n-init+1) x length(la)+1 matrix containing the values of the score test for positive observations for each value of the transformation parameter.

    1st col = fwd search index;

    2nd col = value of the (positive) score test in each step of the fwd search for la(1);

    ...........

    end col = value of the (positive) score test in each step of the fwd search for la(end).

    Note that this output is present only if input option family is 'YJpn' or 'YJall'.
    Scoren

    (n-init+1) x length(la)+1 matrix containing the values of the score test for positive observations for each value of the transformation parameter: 1st col = fwd search index;

    2nd col = value of the (negative) score test in each step of the fwd search for la(1);

    ...........

    end col = value of the (negative) score test in each step of the fwd search for la(end).

    Note that this output is present only if input option family is 'YJpn' or 'YJall'.
    Scoreb

    (n-init+1) x length(la)+1 matrix containing the values of the score test for the joint presence of both constructed variables (associated with positive and negative observations) for each value of the transformation parameter. In this case the reference distribution is the $F$ with 2 and subset_size-p degrees of freedom.

    1st col = fwd search index (subset_size);

    2nd col = value of the score test in each step of the fwd search for la(1);

    ...........

    end col = value of the score test in each step of the fwd search for la(end).

    Note that this output is present only if input option family is 'YJall'
    Scoremle

    (n-init+1) x length(la)+1 matrix containing the values of the (score) likelihood ratio test for the joint presence of both constructed variables (associated with positive and negative observations) for each value of the transformation parameter. In this case the reference distribution is the $F$ with 2 and subset_size-p degrees of freedom.

    1st col = fwd search index (subset_size);

    2nd col = value of the score test in each step of the fwd search for la(1);

    ...........

    end col = value of the score test in each step of the fwd search for la(end).

    Note that this output is present only if input option scoremle is true
    laMLE

    (n-init+1) x 2*length(la)+1 matrix containing the values of the maximum ikelihood estimate of laP and laN.

    Columns 2:3 are associated with the search which has ordered the data using to la(1);

    .........

    Columns 2*length(la):2*length(la)+1 are associated with the search which has ordered the data using to la(length(la)).

    Note that out.laMLE(end,2)=out.laMLE(end,2)=...=out.laMLE(end,2*length(la)) because all these variables contain the MLE of laP based on all the observations. Similarly notice that out.laMLE(end,3)=out.laMLE(end,5)=...=out.laMLE(end,2*length(la)+1) because all these variables contain the MLE of laN based on all the observations. This output is present only if input option scoremle is true.
    la

    vector containing the values of lambda for which fan plot is constructed
    bs

    matrix of size p x length(la) containing the units forming the initial subset for each value of lambda
    Un

    cell of size length(la).

    out.Un{i} is a n-init) x 11 matrix which contains the unit(s) included in the subset at each step in the search associated with la(i).

    REMARK: in every step the new subset is compared with the old subset. Un contains the unit(s) present in the new subset but not in the old one Un(1,:) for example contains the unit included in step init+1 ... Un(end,2) contains the units included in the final step of the search
    class

    'FSRfan'.
    y

    A vector with n elements that contains the response variable which has been used
    X

    Data matrix of explanatory variables which has been used (it also contains the column of ones if input option intercept was missing or equal to 1)

    References

    Atkinson, A.C. and Riani, M. (2000), "Robust Diagnostic Regression Analysis", Springer Verlag, New York.

    Atkinson, A.C. and Riani, M. (2002a), Tests in the fan plot for robust, diagnostic transformations in regression, "Chemometrics and Intelligent Laboratory Systems", Vol. 60, pp. 87-100.

    Atkinson, A.C. Riani, M., Corbellini A. (2019), The analysis of transformations for profit-and-loss data, Journal of the Royal Statistical Society, Series C, "Applied Statistics", https://doi.org/10.1111/rssc.12389

    Atkinson, A.C. Riani, M. and Corbellini A. (2021), The Box–Cox Transformation: Review and Extensions, "Statistical Science", Vol. 36, pp. 239-255, https://doi.org/10.1214/20-STS778

    See Also

    | | | |

    This page has been automatically generated by our routine publishFS