FSRBmdr
FSRBmdr computes minimum deletion residual and other basic linear regression quantities in each step of the Bayesian search.
Syntax
Description
Examples
FSRBmdr with all default options.
Common part to all examples: load Houses Price Dataset.
load hprice.txt;
% setup parameters
n=size(hprice,1);
y=hprice(:,1);
X=hprice(:,2:5);
n0=5;
% set \beta components
beta0=0*ones(5,1);
beta0(2,1)=10;
beta0(3,1)=5000;
beta0(4,1)=10000;
beta0(5,1)=10000;
% \tau
s02=1/4.0e-8;
tau0=1/s02;
% R prior settings
R=2.4*eye(5);
R(2,2)=6e-7;
R(3,3)=.15;
R(4,4)=.6;
R(5,5)=.6;
R=inv(R);
mdrB=FSRBmdr(y,X,beta0,R,tau0,n0);
 FSRBmdr with optional arguments.
FSRBmdr with optional arguments.
 FSRBmdr with optional arguments.
FSRBmdr with optional arguments.
load hprice.txt;
% setup parameters
n=size(hprice,1);
y=hprice(:,1);
X=hprice(:,2:5);
n0=5;
% set \beta components
beta0=0*ones(5,1);
beta0(2,1)=10;
beta0(3,1)=5000;
beta0(4,1)=10000;
beta0(5,1)=10000;
% \tau
s02=1/4.0e-8;
tau0=1/s02;
% R prior settings
R=2.4*eye(5);
R(2,2)=6e-7;
R(3,3)=.15;
R(4,4)=.6;
R(5,5)=.6;
R=inv(R);
mdrB=FSRBmdr(y,X,beta0, R, tau0, n0,'plots',1);
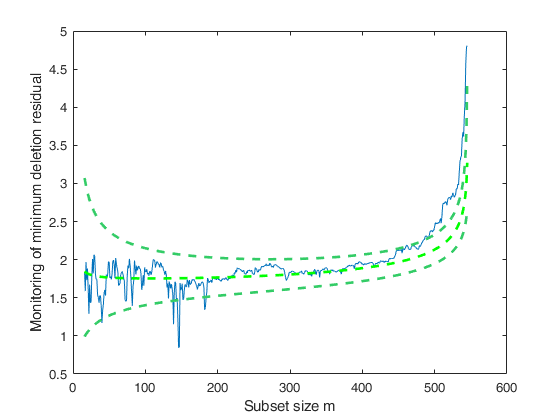
Analyze units entering the search in the final steps.
load hprice.txt;
% setup parameters
n=size(hprice,1);
y=hprice(:,1);
X=hprice(:,2:5);
n0=5;
% set \beta components
beta0=0*ones(5,1);
beta0(2,1)=10;
beta0(3,1)=5000;
beta0(4,1)=10000;
beta0(5,1)=10000;
% \tau
s02=1/4.0e-8;
tau0=1/s02;
% R prior settings
R=2.4*eye(5);
R(2,2)=6e-7;
R(3,3)=.15;
R(4,4)=.6;
R(5,5)=.6;
R=inv(R);
[mdr,Un]=FSRBmdr(y,X,beta0, R, tau0, n0,'plots',1);
Units forming subset in each step.
load hprice.txt;
% setup parameters
n=size(hprice,1);
y=hprice(:,1);
X=hprice(:,2:5);
n0=5;
% set \beta components
beta0=0*ones(5,1);
beta0(2,1)=10;
beta0(3,1)=5000;
beta0(4,1)=10000;
beta0(5,1)=10000;
% \tau
s02=1/4.0e-8;
tau0=1/s02;
% R prior settings
R=2.4*eye(5);
R(2,2)=6e-7;
R(3,3)=.15;
R(4,4)=.6;
R(5,5)=.6;
R=inv(R);
[mdr,Un,BB]=FSRBmdr(y,X,beta0, R, tau0, n0,'plots',1);
Monitor \hat \beta.
load hprice.txt;
% setup parameters
n=size(hprice,1);
y=hprice(:,1);
X=hprice(:,2:5);
n0=5;
% set \beta components
beta0=0*ones(5,1);
beta0(2,1)=10;
beta0(3,1)=5000;
beta0(4,1)=10000;
beta0(5,1)=10000;
% \tau
s02=1/4.0e-8;
tau0=1/s02;
% R prior settings
R=2.4*eye(5);
R(2,2)=6e-7;
R(3,3)=.15;
R(4,4)=.6;
R(5,5)=.6;
R=inv(R);
[mdr,Un,BB,BBayes]=FSRBmdr(y,X,beta0, R, tau0, n0,'plots',1);
 Monitor s^2.
Monitor s^2.
 Monitor s^2.
Monitor s^2.
load hprice.txt;
% setup parameters
n=size(hprice,1);
y=hprice(:,1);
X=hprice(:,2:5);
n0=5;
% set \beta components
beta0=0*ones(5,1);
beta0(2,1)=10;
beta0(3,1)=5000;
beta0(4,1)=10000;
beta0(5,1)=10000;
% \tau
s02=1/4.0e-8;
tau0=1/s02;
% R prior settings
R=2.4*eye(5);
R(2,2)=6e-7;
R(3,3)=.15;
R(4,4)=.6;
R(5,5)=.6;
R=inv(R);
[mdr,Un,BB,BBayes,S2Bayes]=FSRBmdr(y,X,beta0, R, tau0, n0,'plots',1);
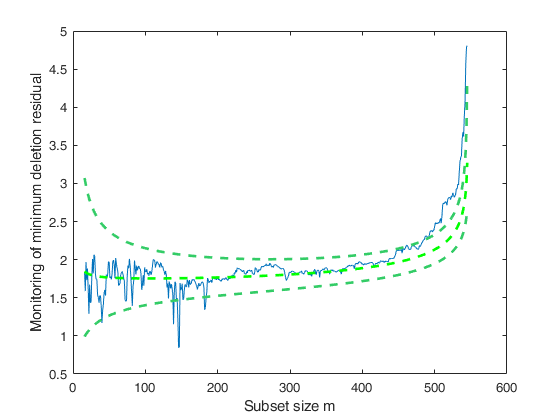
Related Examples
Additional example.
We change n0 from 5 to 250 and impose FSRBmdr monitoring from step 300.
load hprice.txt;
% setup parameters
n=size(hprice,1);
y=hprice(:,1);
X=hprice(:,2:5);
n0=250;
% set \beta components
beta0=0*ones(5,1);
beta0(2,1)=10;
beta0(3,1)=5000;
beta0(4,1)=10000;
beta0(5,1)=10000;
% \tau
s02=1/4.0e-8;
tau0=1/s02;
% R prior settings
R=2.4*eye(5);
R(2,2)=6e-7;
R(3,3)=.15;
R(4,4)=.6;
R(5,5)=.6;
R=inv(R);
mdrB=FSRBmdr(y,X,beta0, R, tau0, n0,'init',300,'plots',1);
Input Arguments
y — Response variable.
Vector.
A vector with n elements that contains the response variable.
Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.
Data Types: single| double
X — Predictor variables.
Matrix.
Data matrix of explanatory variables (also called 'regressors') of dimension (n x p-1).
Rows of X represent observations, and columns represent variables. Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.
PRIOR INFORMATION \beta is assumed to have a normal distribution with mean \beta_0 and (conditional on \tau_0) covariance (1/\tau_0) (X_0'X_0)^{-1}.
\beta \sim N( \beta_0, (1/\tau_0) (X_0'X_0)^{-1} )
Data Types: single| double
R — Matrix associated with covariance matrix of \beta.
p-times-p
positive definite matrix.
It can be interpreted as X_0'X_0 where X_0 is a n0 x p matrix coming from previous experiments (assuming that the intercept is included in the model) The prior distribution of \tau_0 is a gamma distribution with parameters a_0 and b_0, that is p(\tau_0) \propto \tau^{a_0-1} \exp (-b_0 \tau) \qquad E(\tau_0)= a_0/b_0
Data Types: single| double
tau0 — Prior estimate of tau.
Scalar.
Prior estimate of \tau=1/ \sigma^2 =a_0/b_0.
Data Types: single| double
n0 — Number of previous experiments.
Scalar.
Sometimes it helps to think of the prior information as coming from n0 previous experiments. Therefore we assume that matrix X0 (which defines R), was made up of n0 observations.
Data Types: single| double
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'bsb',[3,6,9]
, 'init',100 starts monitoring from step m=100
, 'intercept',false
, 'plots',1
, 'nocheck',true
, 'msg',1
, 'bsbsteps',[10,20,30]
bsb
—units forming initial subset.vector.
m x 1 vector containing the units forming initial subset. The default value of bsb is '' (empty value), that is we initialize the search just using prior information.
Example: 'bsb',[3,6,9]
Data Types: double
init
—Search initialization.scalar.
It specifies the point where to start monitoring required diagnostics. If it is not specified it is set equal to: p+1, if the sample size is smaller than 40;
min(3*p+1,floor(0.5*(n+p+1))), otherwise.
The minimum value of init is 0. In this case in the first step we start monitoring at step m=0 (step just based on prior information)
Example: 'init',100 starts monitoring from step m=100
Data Types: double
intercept
—Indicator for constant term.true (default) | false.
Indicator for the constant term (intercept) in the fit, specified as the comma-separated pair consisting of 'Intercept' and either true to include or false to remove the constant term from the model.
Example: 'intercept',false
Data Types: boolean
plots
—Plot on the screen.scalar.
If equal to one a plot of Bayesian minimum deletion residual appears on the screen with 1%, 50% and 99% confidence bands else (default) no plot is shown.
Remark: the plot which is produced is very simple. In order to control a series of options in this plot and in order to connect it dynamically to the other forward plots it is necessary to use function mdrplot.
Example: 'plots',1
Data Types: double
nocheck
—Check input arguments.boolean.
If nocheck is equal to true no check is performed on matrix y and matrix X. Notice that y and X are left unchanged. In other words the additional column of ones for the intercept is not added. As default nocheck=false.
Example: 'nocheck',true
Data Types: boolean
msg
—Level of output to display.scalar.
It controls whether to display or not messages about great interchange on the screen.
If msg==1 (default) messages are displayed on the screen, else no message is displayed on the screen
Example: 'msg',1
Data Types: double
bsbsteps
—steps of the fwd search where to save the units forming subset.vector.
If bsbsteps is 0 we store the units forming subset in all steps. The default is store the units forming subset in all steps if n<5000, else to store the units forming subset at steps init and steps which are multiple of 100. For example, if n=753 and init=6, units forming subset are stored for m=init, 100, 200, 300, 400, 500 and 600.
Example: 'bsbsteps',[10,20,30]
Data Types: double
Output Arguments
mdrB —Monitoring of minimum
deletion residual at each step of the forward search.
n -by- 2 matrix
1st col = fwd search index (from 0 to n-1).
2nd col = minimum deletion residual.
Un —Unit(s) included
in the subset at each step of the search.
(n-init) -by- 11 Matrix
REMARK: in every step the new subset is compared with the old subset. Un contains the unit(s) present in the new subset but not in the old one.
Un(1,2), for example, contains the unit included in step init+1.
Un(end,2) contains the units included in the final step of the search.
BB —Units belonging to the
subset at each step of the forward search.
n -by- (n-init+1) matrix
1st col = index forming subset in the initial step;
...;
last column = units forming subset in the final step (i.e. all units).
BBayes —posterior estimates of \beta.
Matrix
(n-init+1) x (p+1) matrix containing the monitoring o posterior mean of \beta (regression coefficients) \beta_1 = (c*R + X'X)^{-1} (c*R*\beta_0 + X'y).
S2Bayes —posterior estimate of \sigma^2 and \tau.
Matrix
(n-init+1) x 3 matrix containing the monitoring of posterior estimate of \sigma^2 and \tau in each step of the forward search.
1st col = fwd search index (from init to n).
2nd col = monitoring of \sigma^2_1 (posterior estimate of \sigma^2).
3rd col = monitoring \tau_1 (posterior estimate of \tau). Note that these posterior estimates during the fwd search are corrected using the usual truncated variance consistency factor.
References
Chaloner, K. and Brant, R. (1988), A Bayesian Approach to Outlier Detection and Residual Analysis, "Biometrika", Vol. 75, pp. 651-659.
Riani, M., Corbellini, A. and Atkinson, A.C. (2018), Very Robust Bayesian Regression for Fraud Detection, "International Statistical Review", http://dx.doi.org/10.1111/insr.12247
Atkinson, A.C., Corbellini, A. and Riani, M., (2017), Robust Bayesian Regression with the Forward Search: Theory and Data Analysis, "Test", Vol. 26, pp. 869-886, https://doi.org/10.1007/s11749-017-0542-6