The density of the inverse gamma distribution defined over the support
x>0 with shape parameter a and scale parameter b is
f_{IG}(x, a, b) \propto x^{-a -1} \exp (-b/x)
\frac{b^a}{\Gamma(a)}
inversegampdf computes the gamma pdf at each of the values in x using the
corresponding shape parameters in a and scale parameters in b. Parameters
x, a, and b can be vectors, matrices, or multidimensional arrays that all
have the same size. A scalar input is expanded to a constant array with
the same dimensions as the other inputs. The parameters in a and b must
all be positive and the values in x must be in the interval [0,\infty).
The chief use of the inverse gamma distribution is in Bayesian
statistics, where the distribution arises as the marginal posterior
distribution for the unknown variance of a normal distribution if an
uninformative prior is used; and as an analytically tractable conjugate
prior if an informative prior is required. See the last example below.
Relation with the Gamma distribution.
If X \sim Gamma(a,b) then \frac{1}{X} \sim inverse-gamma distribution
with paramters a and 1/b.
See the appendix of Zellner (1971) for a detailed description of the
inverse Gamma distribution.


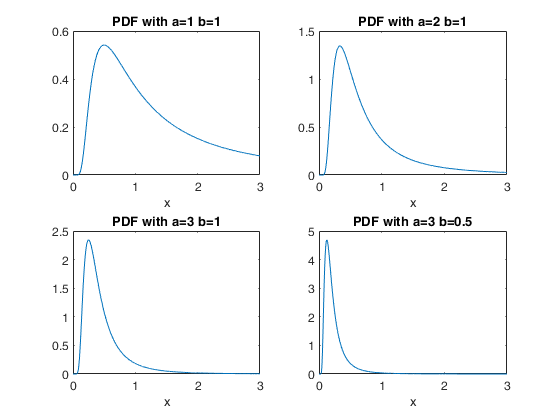
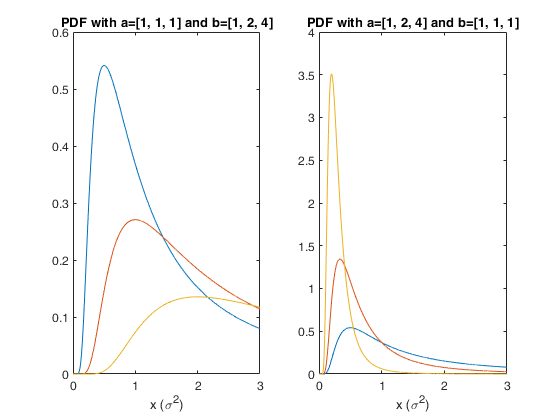
 Plot the pdf for 4 different combinations of parameter values.
Plot the pdf for 4 different combinations of parameter values.