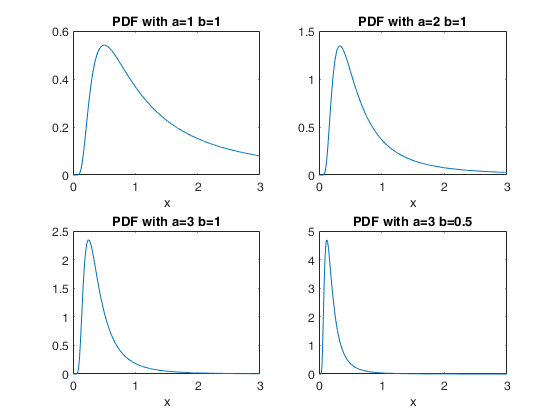
inversegampdf

inversegampdf computes inverse-gamma probability density function.

expand all in page

Syntax

Description

example

y =inversegampdf(x, a, b) Plot the pdf for 4 different combinations of parameter values.

example

y =inversegampdf(x, a, b, nocheck) Compare the results using option nocheck=1.

Examples

expand all

  • Plot the pdf for 4 different combinations of parameter values.

    • x=(0:0.001:3)';
a=[1,2,3,3];
b=[1,1,1,0.5];
for j=1:4
subplot(2,2,j);
plot(x,inversegampdf(x,a(j),b(j)));
xlabel('x');
title(['PDF with a=' num2str(a(j)) ' b=' num2str(b(j))]);
end
    Click here for the graphical output of this example (link to Ro.S.A. website).

  • Compare the results using option nocheck=1.

    • x=(0:0.001:3)';
a=[1,2,3,50,100,10000];
b=[1,10,100,0.05,10,800];
Y=zeros(length(x),length(a));
Ychk=Y;
for i=1:length(x)
Y(i,:)   = inversegampdf(x(i),a,b);
Ychk(i,:)= inversegampdf(x(i),a,b,1);
end
disp('Maximum absolute difference is:');
disp(max(max(abs(Y-Ychk))));
    Maximum absolute difference is:
   2.6049e-09

    Related Examples

    expand all

  • Interpretation in Bayesian statistics.

    • Interpretation of a inverse Gamma (conjugate) prior, used for estimating the posterior distribution of the unknown variance $\sigma{^2}$ of a normal $N(0,\sigma{^2})$. 

    % a set of values for $\sigma^2$
x=(0:0.001:3)';
% Two panels with inverse Gamma distribution for different parameters
% settings.
% Left panel:  fixed shape (1), increasing scale (1,2,4);
% As the scale parameter increases, the mean of the distribution (more 
% and more skewed to the right) also increases. This suggests that an 
% inverse Gamma prior with a larger scale parameter incorporates a prior
% belief in favour of a larger value for $\sigma^2$.
a = [1, 1, 1]; 
b = [1, 2, 4];
subplot(1,2,1);
for j=1:3
plot(x,inversegampdf(x,a(j),b(j)));
hold on;
xlabel('x (\sigma^2)');
end
title('PDF with a=[1, 1, 1] and b=[1, 2, 4]');
% Right panel: fixed scale (1), increasing shape (1,2,4);
% As the shape parameter increases, the distribution becomes more and
% more centered around the mean, producing a tighter set of prior beliefs.   
b = [1, 1, 1]; 
a = [1, 2, 4];
subplot(1,2,2);
for j=1:3
plot(x,inversegampdf(x,a(j),b(j)));
hold on;
xlabel('x (\sigma^2)');
end
title('PDF with a=[1, 2, 4] and b=[1, 1, 1]');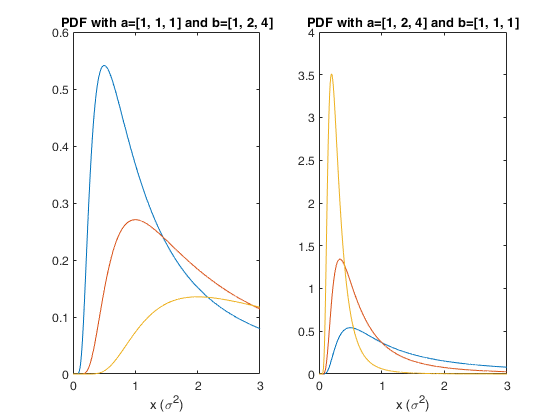
    Click here for the graphical output of this example (link to Ro.S.A. website)

    Input Arguments

    expand all

    x — Value at which the pdf must be evaluated. Scalar, vector or matrix 3D array of the same size of a and b.

    A scalar input functions as a constant matrix of the same size as the other input.

    See "More About:" for details about the inverse gamma distribution.

    Data Types: single | double

    a — shape parameter of the inverse-gamma distribution. Scalar, vector or matrix 3D array of the same size of x and b.

    A scalar input functions as a constant matrix of the same size as the other input.

    See "More About:" for details about the inverse gamma distribution.

    Data Types: single | double

    b — scale parameter b of the inverse-gamma distribution. Scalar, vector or matrix 3D array of the same size of x and a.

    A scalar input functions as a constant matrix of the same size as the other input.

    See "More About:" for details about the inverse gamma distribution.

    Data Types: single | double

    Optional Arguments

    nocheck — Check input arguments. Scalar.

    If nocheck is equal to 1 no check is performed and input and the density is evaluated directly through the expression y = (b.^a).*(x.^(-a-1)).*exp(-b./x)./gamma(a) else we use MATLAB function gampdf.

    Example: 'nocheck',1

    Data Types: double

    Output Arguments

    expand all

    y —Inverse-gamma pdf value. Scalar, vector or matrix or 3D array of the same size of input arguments x, a and b

    $y=f_{IG}(x | a,b)$ is the value of the pdf of the inverse gamma distribution evaluated at x.

    More About

    expand all

    Additional Details

    The density of the inverse gamma distribution defined over the support $x>0$ with shape parameter $a$ and scale parameter $b$ is \[ f_{IG}(x, a, b) \propto x^{-a -1} \exp (-b/x) \frac{b^a}{\Gamma(a)} \]

    inversegampdf computes the gamma pdf at each of the values in x using the corresponding shape parameters in a and scale parameters in b. Parameters x, a, and b can be vectors, matrices, or multidimensional arrays that all have the same size. A scalar input is expanded to a constant array with the same dimensions as the other inputs. The parameters in a and b must all be positive and the values in x must be in the interval $[0,\infty)$.

    The chief use of the inverse gamma distribution is in Bayesian statistics, where the distribution arises as the marginal posterior distribution for the unknown variance of a normal distribution if an uninformative prior is used; and as an analytically tractable conjugate prior if an informative prior is required. See the last example below.

    Relation with the Gamma distribution.

    If $X \sim Gamma(a,b)$ then $\frac{1}{X} \sim$ inverse-gamma distribution with paramters $a$ and $1/b$.

    See the appendix of Zellner (1971) for a detailed description of the inverse Gamma distribution.

    References

    Zellner, A. (1971), "An introduction to Bayesian Inference in Econometrics", Wiley.

    [ https://en.wikipedia.org/wiki/Inverse-gamma_distribution ]

    See Also

    This page has been automatically generated by our routine publishFS