Two-column matrix with the bivariate data
sample on which a probability density estimate is computed. The
density is estimated on a grid of points covering the range of the
data, created using MATLAB function meshgrid.
Data Types: single | double.
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
Example:
'XI',X
, 'Xlim', [Xlim, Ylim]
, 'contourtype','contourf'
, 'cmap',[0, 0, 0.3 ; 0, 0, 0.4 ; 0, 0, 0.5 ]
, 'pdfmethod','fsda'
In this case the density is estimated using X and evaluated on XI.
Example: 'XI',X
Data Types: single | double.
Two-columns matrix
with the bivariate data sample on which the limits of the
probability density estimate is computed. The default value
is [] (i.e. automatic scale).
Example: 'Xlim', [Xlim, Ylim]
Data Types: single | double.
Takes one of these strings:
- contourtype = 'contour' generates a contour plot.
- contourtype = 'contourf' generates a filled contour plot.
- contourtype = 'surf' generates a surf plot.
- contourtype = 'mesh' generates a mesh plot.
Unless specified otherwise, the colormap of the plots is
based on grey levels.
Example: 'contourtype','contourf'
Data Types: char
A personalized colormap is used
to plot the contour. Each row of 'plots' is an RGB triplet
that defines one color or a string which identifies the
color (i.e. 'gray').
Example: 'cmap',[0, 0, 0.3 ; 0, 0, 0.4 ; 0, 0, 0.5 ]
Data Types: single | double | char
Supported options are 'matlab'
and 'fsda'.
- 'matlab' (default) uses the default approach implemented
in the MATLAB ksdensity function, using a normal kernel.
- 'fsda' computes a nonparametric estimate of the
probability density function based on a normal kernel
and using a bandwidth estimated as a function of the
number of points in X.
Independently from the choice of the user, the function
switches automatically to 'fsda' in case the user is using
releases older than R2016a, when function ksdensity was
only addressing one-dimensional data.
Example: 'pdfmethod','fsda'
Data Types: char
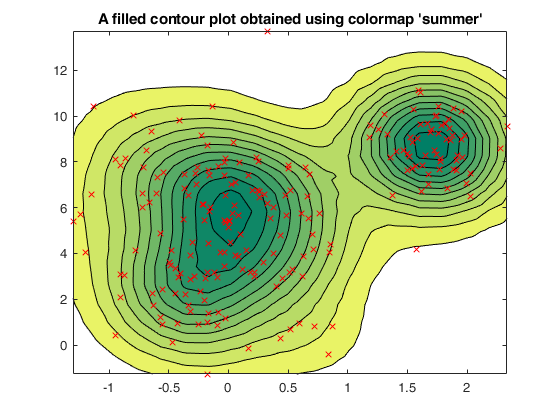
 Density plots for a mixture of two normal distributions.
Density plots for a mixture of two normal distributions.