logmvnpdfFS
logmvnpdfFS produces log of Multivariate normal probability density function (pdf)
Syntax
y=logmvnpdfFS(X, Mu, Sigma)exampley=logmvnpdfFS(X, Mu, Sigma, X0)exampley=logmvnpdfFS(X, Mu, Sigma, X0, eyed)exampley=logmvnpdfFS(X, Mu, Sigma, X0, eyed, n)exampley=logmvnpdfFS(X, Mu, Sigma, X0, eyed, n, d)exampley=logmvnpdfFS(X, Mu, Sigma, X0, eyed, n, d, msg)exampley=logmvnpdfFS(X, Mu, Sigma, X0, eyed, n, d, msg, callmex)example
Description
This function is a much faster version than (log of) Matlab function mvnpdf. If this function is called without optional arguments than it uses matlab function bsxfun to compute the deviations form the means and no mex function.
If this function is called with the four optional input arguments X0, eyed, n and d a mex function based on C code is directly used.
Additional details follow: in order to compute the kernel of the quadratic form at the exponent logmvnpdfFS creates an identity of size length(Mu) and similarly needs to compute length(Mu). These two quantites can be precalculated and supplied as input parameters. If logmvnpdfFS has to be called thousands of times (as it happens for example in each iteration of all procedures of cluster analysis based mixtures of multivariate gaussian distributions). The same argument above applies to scalars n and d which are directly passed to the compiled mex function
Examples
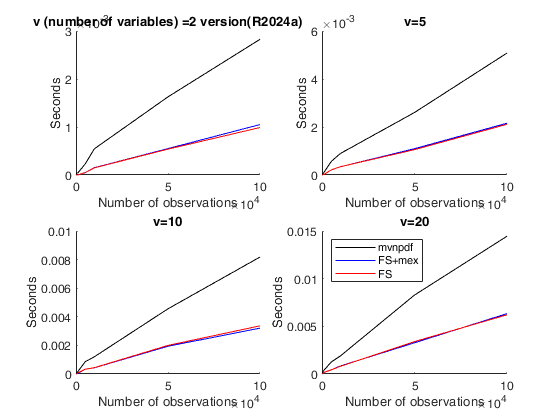
 TIME COMPARISON USING TIMEIT FUNCTION.
TIME COMPARISON USING TIMEIT FUNCTION.