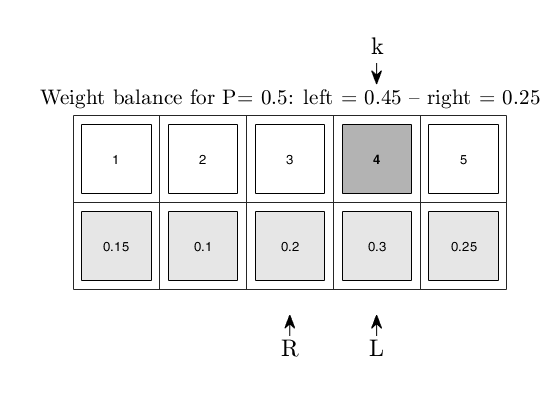
quickselectFSw_demo
quickselectFSw_demo illustrates the functioning of quickselectFSw
Syntax
Description
Examples
Input Arguments
Output Arguments
References
Azzini, I., Perrotta, D. and Torti, F. (2023), A practically efficient fixed-pivot selection algorithm and its extensible MATLAB suite, "arXiv, stat.ME, eprint 2302.05705"
 quickselectFSw without optional parameter p gives the weighted
median.
quickselectFSw without optional parameter p gives the weighted
median.