rthin

rthin applies independent random thinning to a point pattern.

expand all in page

Syntax

Description

This function was ported to matlab from the R spatstat package, developed by Adrian Baddeley (Adrian.Baddeley@curtin.edu.au), Rolf Turner (r.turner@auckland.ac.nz) and Ege Rubak (rubak@math.aau.dk) for the statistical analysis of spatial point patterns. The algorithm for random thinning was changed in spatstat version 1.42-3. Our matlab porting is based on a earlier version. See the rthin documentation in spatstat for more details.

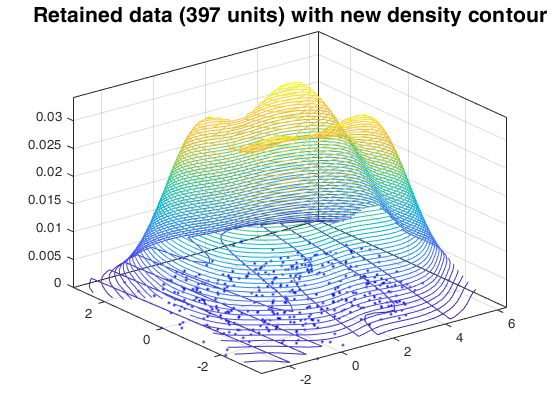
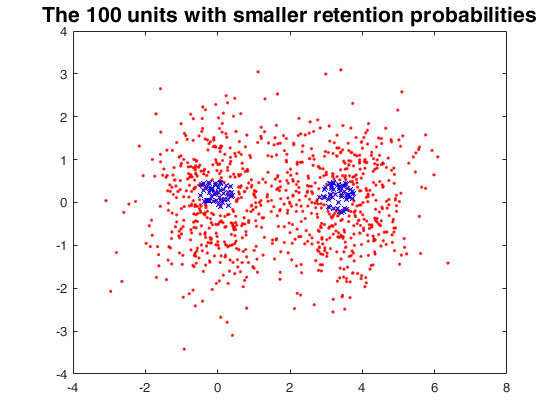
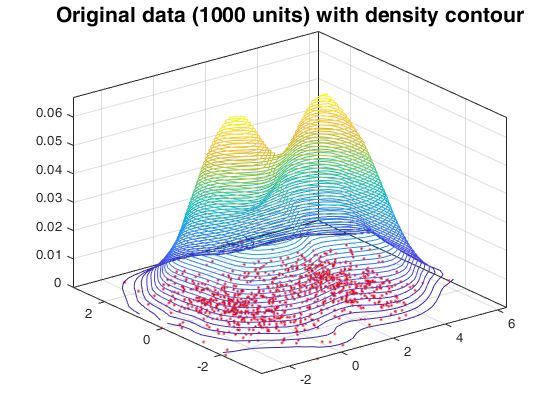
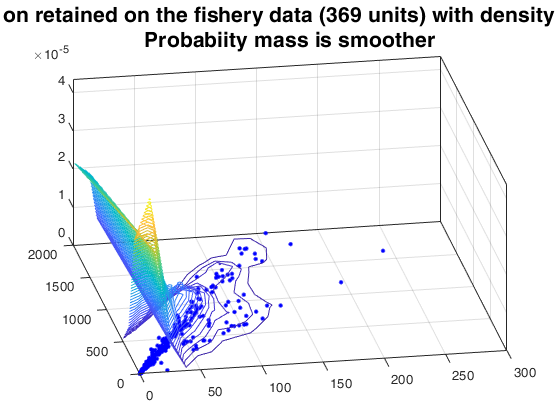
In a random thinning operation, each point of X is randomly either deleted or retained (i.e. not deleted). The result is a point pattern, consisting of those points of X that were retained. Independent random thinning means that the retention/deletion of each point is independent of other points.

example

Y =rthin(X, P) Random thinning on a mixture of normal distribution.

example

[Y , retain] =rthin(___) Random thinning on the fishery dataset.

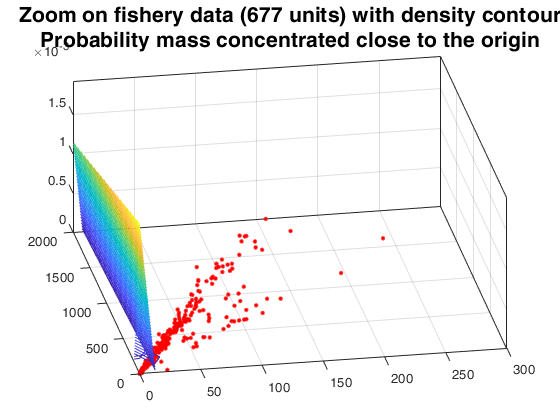
Examples

expand all

  • Random thinning on a mixture of normal distribution.

    • Data 

    clear all; close all;
data=[randn(500,2);randn(500,1)+3.5, randn(500,1);];
x = data(:,1);
y = data(:,2);
% Data density
[density,xout,bandwidth]   = kdebiv(data,'pdfmethod','fsda');
xx = xout(:,1);
yy = xout(:,2);
zz = density;
% plot of data and density
figure;
[xq,yq] = meshgrid(xx,yy);
density = griddata(xx,yy,density,xq,yq);
contour3(xq,yq,density,50), hold on
plot(x,y,'r.','MarkerSize',5)
title(['Original data (' num2str(numel(y)) ' units) with density contour'],'FontSize',16);
%Interpolate the density and apply thinning using retention probabilities (1 - pdfe/max(pdfe))
F = TriScatteredInterp(xx(:),yy(:),zz(:));
pdfe = F(x,y);
pretain = 1 - pdfe/max(pdfe);
[Xt , Xti]= rthin([x y],pretain);
% rthin retention probabilities
[psorted ii] = sort(pretain);
figure;
plot(x,y,'r.','MarkerSize',5);
hold on;
plot(x(ii(1:100)),y(ii(1:100)),'bx','MarkerSize',5);
title('The 100 units with smaller retention probabilities','FontSize',16);
% now estimate the density on the retained units
%[tdensity,txout,tbandwidth] = ksdensity(Xt);
[tdensity,txout,tbandwidth]  = kdebiv(Xt,'pdfmethod','fsda');
txx = txout(:,1);
tyy = txout(:,2);
tzz = tdensity;
% and plot the retained units with their density superimposed
figure;
[txq,tyq] = meshgrid(txx,tyy);
tdensity = griddata(txx,tyy,tdensity,txq,tyq);
contour3(txq,tyq,tdensity,50), hold on
plot(x(Xti),y(Xti),'b.','MarkerSize',5);
title(['Retained data (' num2str(numel(y(Xti))) ' units) with new density contour'],'FontSize',16);
cascade;
    Click here for the graphical output of this example (link to Ro.S.A. website).

  • Random thinning on the fishery dataset.

    • load data and add some jittering, because duplicated units are not treated 

    clear all; close all;
load('fishery.txt');
fishery = fishery + 10^(-8) * abs(randn(677,2));
x = fishery(:,1);
y = fishery(:,2);
% Data density
[density,xout,bandwidth]   = kdebiv(fishery,'pdfmethod','fsda');
xx = xout(:,1);
yy = xout(:,2);
zz = density;
% plot of data and density
figure;
[xq,yq] = meshgrid(xx,yy);
density = griddata(xx,yy,density,xq,yq);
contour3(xq,yq,density,50), hold on
plot(x,y,'r.','MarkerSize',8)
xlim([0 300]); ylim([0 2000]);
set(gca,'CameraPosition',[-216 -12425 0.0135]);
title({['Zoom on fishery data (' num2str(numel(y)) ' units) with density contour'] , 'Probability mass concentrated close to the origin'},'FontSize',16);
%Interpolate the density and apply thinning using retention
%probabilities equal to 1 - pdfe/max(pdfe)
F = TriScatteredInterp(xx(:),yy(:),zz(:));
pdfe = F(x,y);
pretain = 1 - pdfe/max(pdfe);
[Xt , Xti]= rthin([x y],pretain);
% now estimate the density on the retained units
[tdensity,txout,tbandwidth]  = kdebiv(Xt,'pdfmethod','fsda');
txx = txout(:,1);
tyy = txout(:,2);
tzz = tdensity;
% and plot the retained units with their density superimposed
figure;
[txq,tyq] = meshgrid(txx,tyy);
tdensity = griddata(txx,tyy,tdensity,txq,tyq);
contour3(txq,tyq,tdensity,50), hold on
plot(x(Xti),y(Xti),'b.','MarkerSize',8);
xlim([0 300]); ylim([0 2000]);
set(gca,'CameraPosition',[-216 -12425 0.0002558 ]);
title({['Zoom on retained on the fishery data (' num2str(numel(y(Xti))) ' units) with density contour'] , 'Probabiity mass is smoother'},'FontSize',16);
cascade;
    Click here for the graphical output of this example (link to Ro.S.A. website).

    Input Arguments

    expand all

    X — Vector with the data to be thinned. Data can represent a point pattern.

    Data Types: single| double

    P — Vector giving the retention probabilities, i.e. the probability that each point in X will be retained.

    It can be: - a single number, so that each point will be retained with the same probability P;

    - a vector of numbers, so that the ith point of X will be retained with probability P(i);

    - a function P(x,y), so that a point at a location (x,y) will be retained with probability P(x,y);

    - a pixel image, containing values of the retention probability for all locations in a region encompassing the point pattern.

    If P is a function, it should be vectorised, that is, it should accept vector arguments x,y and should yield a numeric vector of the same length. The function may have extra arguments which are passed through the argument.

    Data Types: single| double

    Output Arguments

    expand all

    Y —the retained data units. Vector

    In practice, Y = X(retain,:).

    retain —the indices of the retained points in the original data X. Vector

    The ith point of X is retained with probability P(i).

    Optional Output:

    References

    Bowman, A.W. and Azzalini, A. (1997), "Applied Smoothing Techniques for Data Analysis", Oxford University Press.

    Acknowledgements

    This function was ported to matlab from the R spatstat package, developed by Adrian Baddeley (Adrian.Baddeley@curtin.edu.au), Rolf Turner (r.turner@auckland.ac.nz) and Ege Rubak (rubak@math.aau.dk) for the statistical analysis of spatial point patterns. The algorithm for random thinning was changed in spatstat version 1.42-3. Our matlab porting is based on a previous version. See the rthin documentation in spatstat for more details.

    See Also

    This page has been automatically generated by our routine publishFS