subsets
subsets creates a matrix of indexes where rows are distinct p-subsets extracted from a set of n elements
Syntax
Description
Examples
 Create a matrix with the indexes of 5 subsets when n=100, p=3.
Create a matrix with the indexes of 5 subsets when n=100, p=3.
 Create a matrix with the indexes of 5 subsets when n=100, p=3.
Create a matrix with the indexes of 5 subsets when n=100, p=3.Only default arguments used.
C = subsets(5,100,3)
C = 5×3 int8 matrix 15 27 60 59 90 92 55 84 92 14 55 60 78 83 91
 Create a matrix with the indexes of 5 subsets when n=100, p=3.
Create a matrix with the indexes of 5 subsets when n=100, p=3.
 Create a matrix with the indexes of 5 subsets when n=100, p=3.
Create a matrix with the indexes of 5 subsets when n=100, p=3.Use information on the number of combinations to speed up generation.
ncomb = bc(100,3);
C = subsets(5,100,3,ncomb)
C =
5×3 int8 matrix
20 71 99
17 76 79
42 52 53
8 13 76
32 74 80
 Create a matrix with the indexes of 5 subsets when n=100, p=3.
Create a matrix with the indexes of 5 subsets when n=100, p=3.
 Create a matrix with the indexes of 5 subsets when n=100, p=3.
Create a matrix with the indexes of 5 subsets when n=100, p=3.Also inform about the time taken for the operation.
ncomb = bc(1000,5);
C = subsets(500000,1000,5,ncomb,1);
Warning: you have specified to extract more than 100000 subsets To iterate so many times may be lengthy
Create a matrix with the indexes of 5 subsets when n=100, p=3.
As the previous example, but in addition returns in nselected the number of combinations.
ncomb = bc(1000,5);
[C , nselected] = subsets(500000,1000,5,ncomb,1);
Related Examples
 Sampling without replacement and the hypergeometric distribution.
Sampling without replacement and the hypergeometric distribution.
 Sampling without replacement and the hypergeometric distribution.
Sampling without replacement and the hypergeometric distribution.
clear all; close all;
% parameters
n = 100;
p = 3;
nsamp = 1000000;
ncomb = bc(n,p);
msg = 0;
% Sampling without repetition nsamp p-subsets from a dataset of n units.
C = subsets(nsamp, n, p, ncomb, msg);
if verLessThan('matlab','8.4')
hist(double(C(:))); xlim([1 n]);
else
histogram(double(C(:)),'Normalization','pdf','BinMethod','Integers'); xlim([1 n]);
% this superimposes a line with the unit counts
frC = tabulateFS(double(C(:)));
hold on; plot(1:n,frC(:,3)/100,'r-','LineWidth',3);
end
% The hypergeometric distribution hygepdf(X,M,K,N) computes the probability
% of drawing exactly X of a possible K items in N drawings without
% replacement from a group of M objects. For drawings with replacement,
% the distribution would be binomial.
hpdf = hygepdf(0:p,n,n/2,p);
% Say that the n/2 target items (which determine the success of a draw) are
% in the subset formed by units 1,2,...n/2. Let's then count how many times
% we get units from this group.
c = C<=n/2;
sc = sum(c,2);
tab = tabulateFS(sc);
tab = (tab(:,2)/sum(tab(:,2)))';
disp('Probability of getting 0 to p successes in p drawns (hypergeometric pdf):');
disp(hpdf);
disp('Frequencies of the 0 to p successes in the p drawns (subsets output):');
disp(tab);
Warning: number of subsets which have been chosen (1000000) are greater than possibile number (161700)
All subsets are extracted
Probability of getting 0 to p successes in p drawns (hypergeometric pdf):
0.1212 0.3788 0.3788 0.1212
Frequencies of the 0 to p successes in the p drawns (subsets output):
0.1212 0.3788 0.3788 0.1212
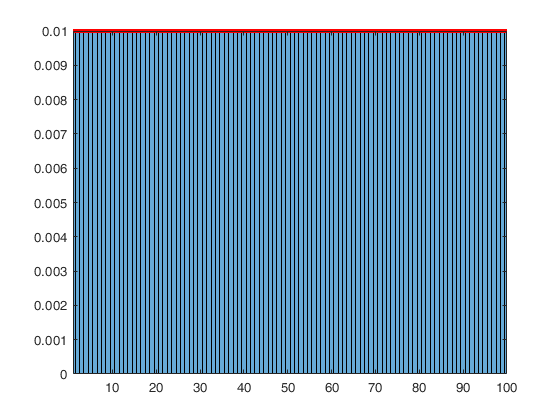
 Weighted sampling without replacement and the non-central Wallenius hypergeometric distribution.
Weighted sampling without replacement and the non-central Wallenius hypergeometric distribution.
 Weighted sampling without replacement and the non-central Wallenius hypergeometric distribution.
Weighted sampling without replacement and the non-central Wallenius hypergeometric distribution.
clear all; close all;
% parameters
n = 500;
p = 3;
nsamp = 50000;
ncomb = bc(n,p);
msg = 0;
% Sampling probability of the first n/2 units is 10 times larger than the others n/2.
method = [10*ones(n/2,1); ones(n/2,1)];
% no need to normalize weights: method = method(:)' / sum(method);
C = subsets(nsamp, n, p, ncomb, msg, method);
if verLessThan('matlab','8.4')
hist(double(C(:))); xlim([1 n]);
else
histogram(double(C(:)),'Normalization','pdf','BinMethod','Integers');
end
% Here we address the case when the sampling (without replacement) is biased,
% in the sense that the probabilities to select the units in the sample are
% proportional to weights provided using option 'method'. In this case, the
% extraction probabilities follow Wallenius' noncentral hypergeometric
% distribution. The sampling scheme is the same of that of the hypergeometric
% distribution but, in addition, the success and failure are associated with
% weights w1 and w2 and we will say that the odds ratio is odds = w1 / w2. The
% function is then called as: wpdf = WNChygepdf(x,M,K,n,odds).
for i = 0:p
wpdf(i+1) = WNChygepdf(i,n,n/2,p,10);;
end
% counts of the actual samples
c = C<=n/2;
sc = sum(c,2);
tab = tabulateFS(sc);
tab = (tab(:,2)/sum(tab(:,2)))';
disp('Probability of getting 0 to p successes in p weighted drawns (non-central hypergeometric pdf):');
disp(wpdf);
disp('Frequencies of the 0 to p successes in the p weighted drawns (subsets output):');
disp(tab);
% The non-central hypergeometric is also available in the R package
% BiasedUrn. In the example above, where there are just two groups and one
% weight defining the ratio between the units in the two groups, the function
% to use is dWNCHypergeo (for Wallenius' distribution):
%
% dWNCHypergeo(c(0,1,2,3), 50, 50, 3, 10)
% [1] 0.0007107089 0.0225823308 0.2296133830 0.7470935773
%
% The general syntax of the function is:
% dWNCHypergeo(x, m1, m2, n, odds)
% x = Number of red balls sampled.
% m1 = Initial number of red balls in the urn.
% m2 = Initial number of white balls in the urn.
% n = Total number of balls sampled.
% N = Total number of balls in urn before sampling.
% odds = Probability ratio of red over white balls.
% p = Cumulative probability.
% nran = Number of random variates to generate.
% mu = Mean x.
% precision = Desired precision of calculation.
Probability of getting 0 to p successes in p weighted drawns (non-central hypergeometric pdf):
0.0007 0.0225 0.2262 0.7505
Frequencies of the 0 to p successes in the p weighted drawns (subsets output):
0.0007 0.0221 0.2289 0.7483
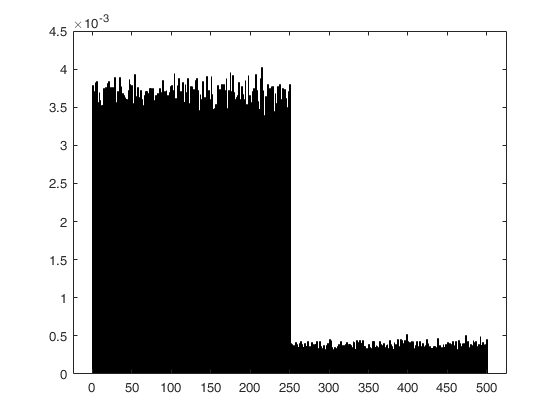
Weighted sampling without replacement, with negative weights.
clear all; close all;
n = 200;
p = 3;
nsamp = 10000;
ncomb = bc(n,p);
msg = 0;
method = [-4*ones(n/4,1); -2*ones(n/4,1) ; -1*ones(n/4,1); -4*ones(n/4,1)];
C = subsets(nsamp, n, p, ncomb, msg, method);
if verLessThan('matlab','8.4')
hist(double(C(:))); xlim([1 n]);
else
histogram(double(C(:)),'Normalization','pdf','BinMethod','Integers');
end
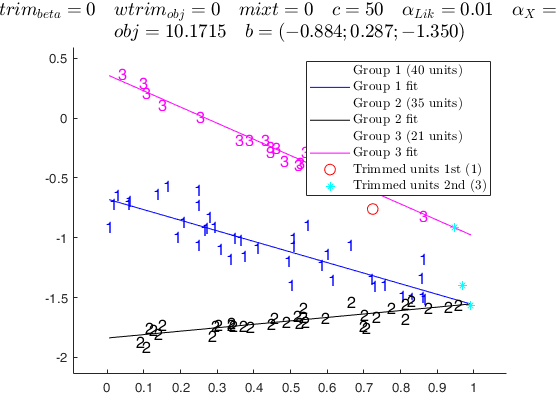
 Function subset used in clustering or mixture modeling simulations.
Function subset used in clustering or mixture modeling simulations.
 Function subset used in clustering or mixture modeling simulations.
Function subset used in clustering or mixture modeling simulations.
clear all; close all;
% parameters
n = 100; %number of units
p = 2; %number of variables
k = 3; %number of groups
nsamp = 500; %number of samples
ncomb = bc(n,p);
msg = 0;
% A dataset simulated using MixSim
rng(372,'twister');
Q=MixSimreg(k,p,'BarOmega',0.001);
[y,X,id]=simdatasetreg(n,Q.Pi,Q.Beta,Q.S,Q.Xdistrib);
% Some user-defined weights for weighted sampling, provided as a vector of "method" option.
method = [1*ones(n/2,1); ones(n/2,1)];
% C must be a nsamp-by-k*p matrix, to contain the extraction of nsamp p-combinations k times.
% This can be easily done as follows:
for i=1:k
Ck(:,(i-1)*p+1:i*p) = subsets(nsamp, n, p, ncomb, msg, method);
end
% Ck is then provided, e.g., to tclustreg as follows:
out=tclustreg(y,X,k,50,0.01,0.01,'nsamp',Ck);
Warning: columns 1 2 are constant and just col 1 has been kept! ClaLik with untrimmed units selected using crisp criterion Total estimated time to complete tclustreg: 1.42 seconds
Input Arguments
nsamp — Number of subsamples which have to be extracted.
Scalar;
if nsamp=0 all subsets will be extracted; they will be (n
choose p).
Data Types: single|double
p — Size of the subsets.
Scalar.
In regression with p explanatory variable the size of the elmental subsets is p;
in multivariate analysis, in presence of v variables, the size of the elemental subsets is v+1.
Data Types: single|double
Optional Arguments
ncomb — scalar (n choose p).
If the user has already computed this
value it can supply it directly, otherwise the program will
calculate it automatically.
Example: C=subsets(20,10,3,120)
Data Types: single|double
msg — scalar which controls whether to display or not messages
on the screen.
If msg=true (default), messages are displayed
on the screen about estimated time.
Example: C=subsets(20,10,3,120,0)
Data Types: boolean
method — Sampling methods.
Scalar or vector.
Methods used to extract the subsets. See section 'More About' of function randsampleFS for details about the sampling methods. Default is method = 1.
- Scalar, from 0 to 3 determining the (random sample without replacement) method to be used.
- Vector of weights: in such a case, Weighted Sampling Without Replacement is applied using that vector of weights.
Example: randsampleFS(100,10,2)
Data Types: single|double
Output Arguments
C —The indices of the subsets which need to be extracted.
Matrix with nselected rows and p columns (stored in int16 format)
Data Types - single|double
References
Wong, C.K. and M.C. Easton (1980) "An Efficient Method for Weighted Sampling Without Replacement", SIAM Journal of Computing, 9(1):111-113.
See Also
randsampleFS
|
lexunrank
|
bc