FSMenvmmd

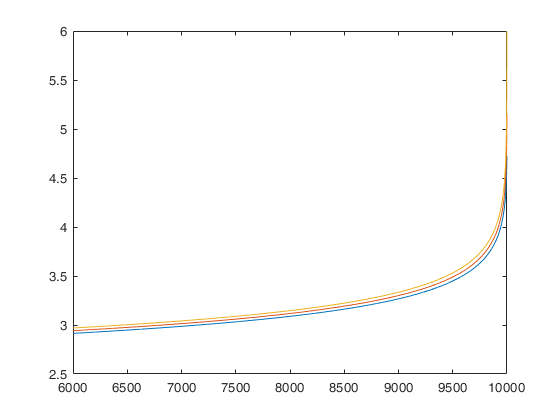
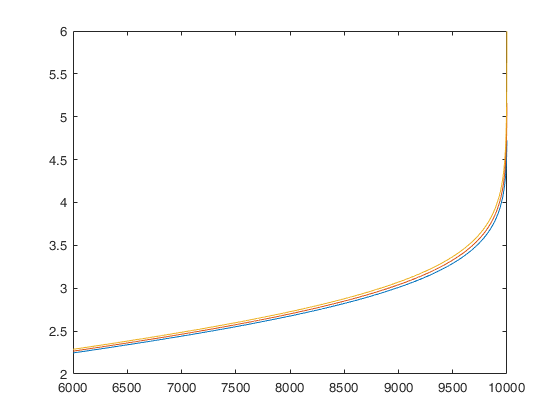
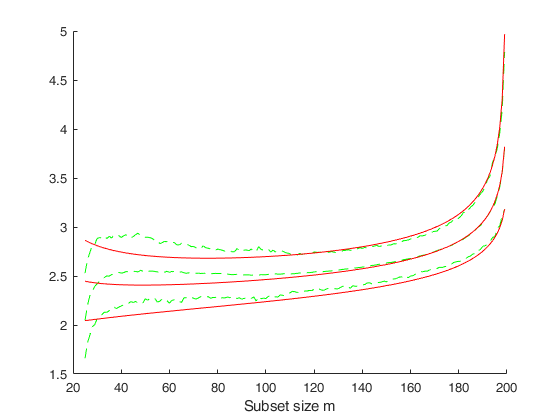
FSMenvmmd computes the theoretical envelopes of Minimum MD outside subset during the search

expand all in page

Syntax

  • MMDenv=FSMenvmmd(n,v)example
  • MMDenv=FSMenvmmd(n,v,Name,Value)example

Description

example

MMDenv =FSMenvmmd(n, v) FSMenvmmd with all default options.

example

MMDenv =FSMenvmmd(n, v, Name, Value) FSMenvmmd with otpional arguments.

Examples

expand all

  • FSMenvmmd with all default options.

    • Example of creation of 1 per cent, 50 per cent and 99 per cent envelopes based on 10000 observations and 5 explanatory variables. 

    MMDenv=FSMenvmmd(10000,5);
plot(MMDenv(:,1),MMDenv(:,2:end))
    Click here for the graphical output of this example (link to Ro.S.A. website).

  • FSMenvmmd with otpional arguments.

    • Example of creation of 1 per cent, 50 per cent and 99 per cent envelopes based on 10000 observations and 5 explanatory variables. The envelopes are produced for scaled Mahalanobis distances (no consistency factor is applied) 

    MMDenv=FSMenvmmd(10000,5,'scaled',1);
plot(MMDenv(:,1),MMDenv(:,2:end))
    Click here for the graphical output of this example (link to Ro.S.A. website).

    Related Examples

    expand all

  • Order statistics and simulations envelopes .

    • In this example we compare the accuracy of the envelopes computed with order statistics with those which come from simulations. 

    % Fix a seed
state=1000;
mtstream = RandStream('shr3cong','Seed',state);
RandStream.setGlobalStream(mtstream);
defaultStream = RandStream.getGlobalStream();
reset(defaultStream)
% If you run this example in a version older than 7.9 replace the previous
% four lines with
% randn('state', 1000);
n=200;
p=3;
init=25;
nsimul=1000;
mmdStore=zeros(n-init,nsimul);
for j=1:nsimul
Y=randn(n,p);
[fre]=unibiv(Y);
%create an initial subset with the 20 observations with the lowest
%Mahalanobis Distance
fre=sortrows(fre,4);
bs=fre(1:25,1);
mmd = FSMmmd(Y,bs,'init',init);
mmdStore(:,j)=mmd(:,2);
end
% Sort rows of matrix mmdStore
mmdStore=sort(mmdStore,2);
% Create figure which compares empirical and theoretical forward envelopes
% for minimum deletion residual
figure;
hold('on');
quant=[0.01 0.5 0.99];
sel=round(nsimul*quant);
% Plot lines of empirical quantiles
line(mmd(:,1),mmdStore(:,sel),'LineStyle','--','Color','g');
% Plots lines of theoretical quantiles using order statistics
mmdT=FSMenvmmd(n,p,'init',init);
line(mmdT(:,1),mmdT(:,2:4),'LineStyle','-','Color','r');
xlabel('Subset size m');
    Click here for the graphical output of this example (link to Ro.S.A. website)

    Input Arguments

    expand all

    n — Number of observations. Scalar.

    Number of observations.

    Data Types: single | double

    v — Number of variables. Scalar.

    Number of variables.

    Data Types: single | double

    Name-Value Pair Arguments

    Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

    Example: 'init',50 , 'prob',[0.05 0.95] , 'scaled',false

    init —Point where to start monitoring required diagnostics.scalar.

    Note that if bsb is supplied, init>=length(bsb). If init is not specified it will be set equal to floor(n*0.6).

    Example: 'init',50

    Data Types: double

    prob —quantiles for which envelopes have to be computed.vector.

    Vector containing 1 x k elements .

    The default is to produce 1 per cent, 50 per cent and 99 per cent envelopes.

    Example: 'prob',[0.05 0.95]

    Data Types: double

    scaled —It indicates how to compute the envelopes.boolean.

    If scaled=true0 the envelopes are produced for scaled Mahalanobis distances (no consistency factor is applied) else the traditional consistency factor is applied (this is the default)

    Example: 'scaled',false

    Data Types: logical

    Output Arguments

    expand all

    MMDenv —Envelopes for the requested quantiles. n-m0+1 x length(prob)+1 columns

    1st col = fwd search index from m0 to n-1;

    2nd col = envelope for quantile prob[1];

    3rd col = envelope for quantile prob[2];

    ...;

    (k+1) col = envelope for quantile prob[k].

    References

    Riani, M., Atkinson, A.C. and Cerioli, A. (2009), Finding an unknown number of multivariate outliers, "Journal of the Royal Statistical Society Series B", Vol. 71, pp. 201-221.

    See Also

    |

    This page has been automatically generated by our routine publishFS