n x 1
vector containing residuals or Mahalanobis distances
for the n units of the sample
Data Types: single| double
Scalar or vector of
length 4 which specifies the value of the tuning
constant c (scalar greater than 0 which controls the
robustness/efficiency of the estimator)
and the prefixed values of paramters a, b, c
ctuning(1) = tuning constant which will multiply
parameters a, b and c of Hampel rho (psi) function
ctuning(2) = paramter a of Hampel rho (psi) function
ctuning(3) = paramter b of Hampel rho (psi) function
ctuning(4) = paramter c of Hampel rho (psi) function
Remark: if length(ctuning)==1 values of a, b and c will be
set to a=2*ctuning b=4*ctuning c=4*ctuning
With these choices, if ctuning=1 the
resulting influence function is nearly identical to the
biweight with parameter 8.
Data Types: single| double
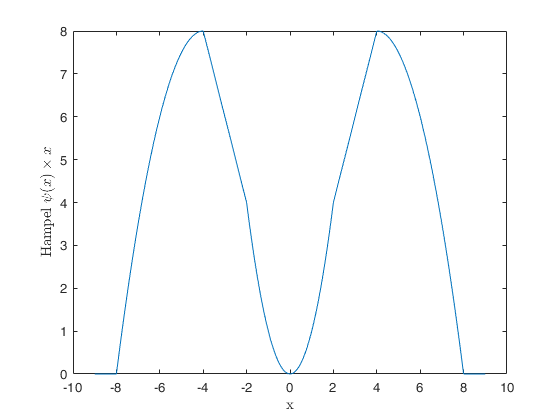
 Plot of psi(x) multiplied by x.
Plot of psi(x) multiplied by x.