Heston1D
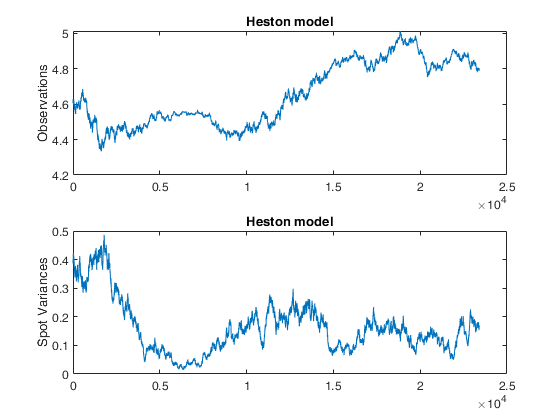
Heston1D simulates observations and instantaneous variances from the Heston model
Syntax
Description
Heston1D simulates, using the Euler–Maruyama method, observations and instantaneous variances from the model by [S. Heston, The Review of Financial Studies, Vol. 6, No. 2, 1993].
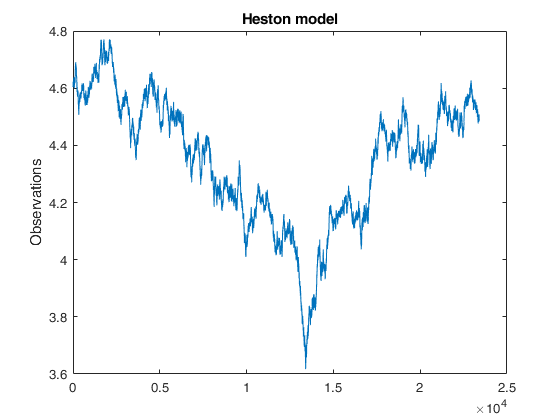
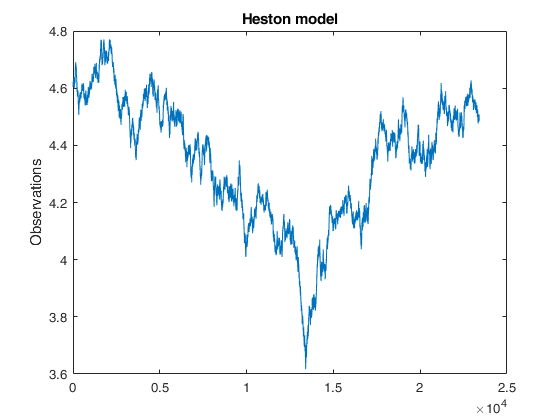
Example of call of Heston1D for obtaining process observations only.x
=Heston1D(T,
n,
parameters,
rho,
x0,
V0)
Examples
Input Arguments
Output Arguments
More About
References
Heston, S. (1993), A closed-form solution for options with stochastic volatility with applications to bond and currency options, The Review of Financial Studies, Vol. 6, No. 2.
 Example of call of Heston1D for obtaining process observations only.
Example of call of Heston1D for obtaining process observations only.