mcd
mcd computes Minimum Covariance Determinant
Syntax
Description
Examples
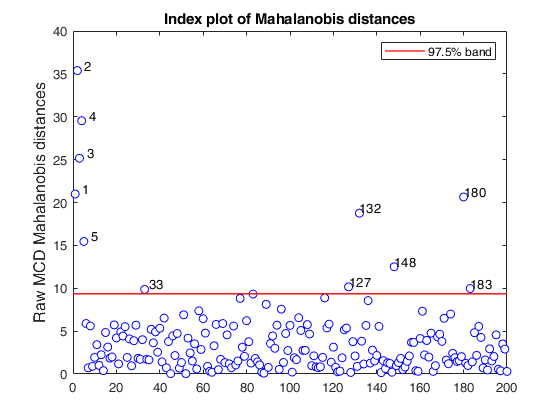
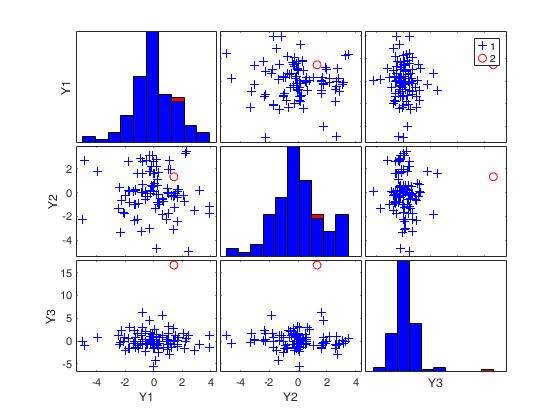
mcd with all default options.
n=200;
v=3;
randn('state', 123456);
Y=randn(n,v);
% Contaminated data
Ycont=Y;
Ycont(1:5,:)=Ycont(1:5,:)+3;
RAW=mcd(Ycont);
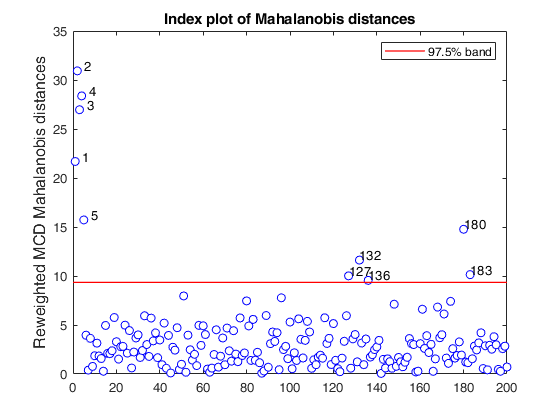
mcd monitoring the reweighted estimates.
n=200;
v=3;
randn('state', 123456);
Y=randn(n,v);
% Contaminated data
Ycont=Y;
Ycont(1:5,:)=Ycont(1:5,:)+3;
[RAW,REW]=mcd(Ycont);
mcd monitoring the exctracted subsamples.
n=200;
v=3;
randn('state', 123456);
Y=randn(n,v);
% Contaminated data
Ycont=Y;
Ycont(1:5,:)=Ycont(1:5,:)+3;
[RAW,REW,C]=mcd(Ycont);
Related Examples
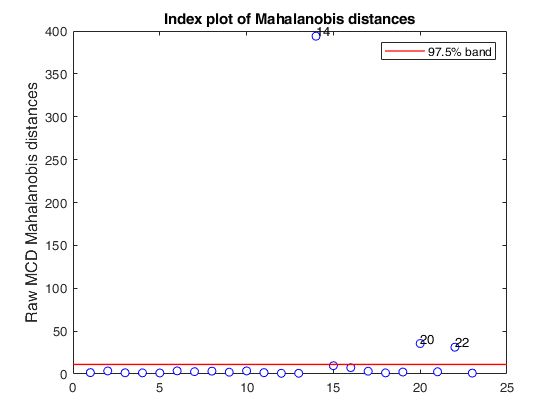
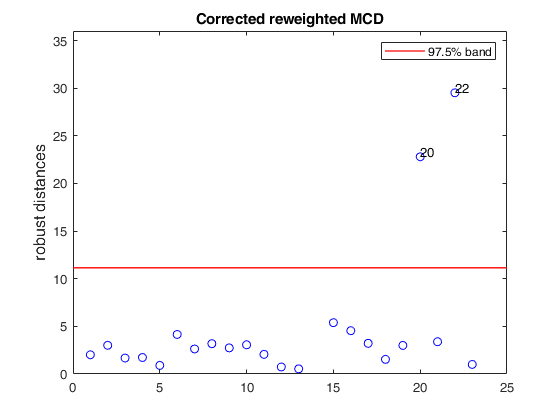
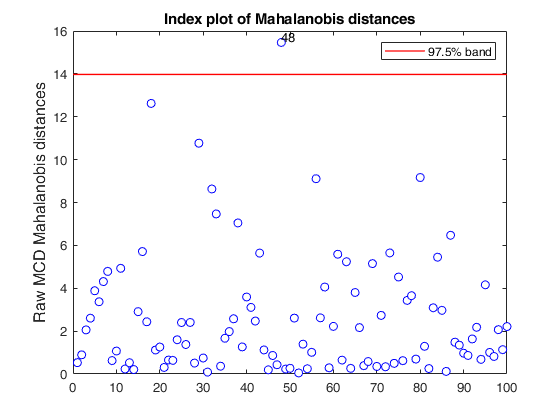
 mcd applied to the aircraft data (plots using the scale of Pison et al).
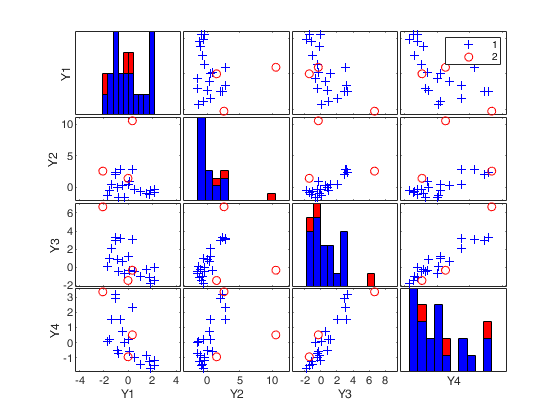
mcd applied to the aircraft data (plots using the scale of Pison et al).
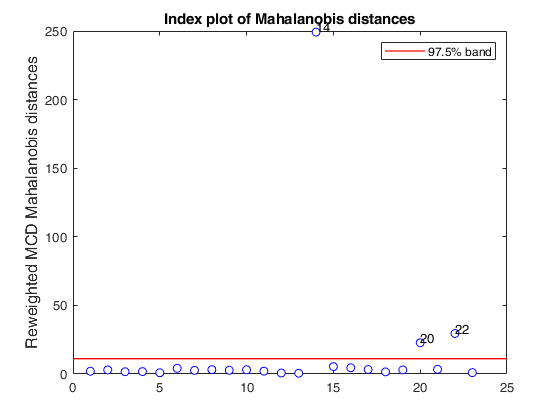
 mcd applied to the aircraft data (plots using the scale of Pison et al).
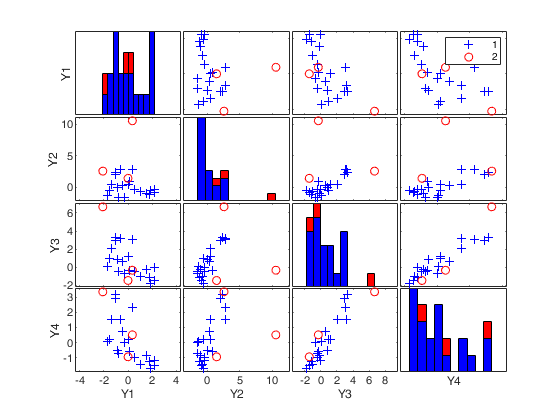
mcd applied to the aircraft data (plots using the scale of Pison et al).See Pison et al. 2002, Metrika.
X = load('aircraft.txt');
Y = X(:,1:end-1);
[RAW,REW] = mcd(Y,'bdp',0.25,'ysaveRAW',1);
v=size(Y,2);
% Compare the following figure with panel (b) of Fig. 8 of Pison et al.
ylimy=[0 36];
malindexplot(RAW.md,v,'conflev',0.975,'laby','robust distances','numlab',RAW.outliers,'ylimy',ylimy);
title('Corrected MCD')
% Compare the following figure with panel (4) of Fig. 8 of Pison et al.
ylimy=[0 36];
malindexplot(REW.md,v,'conflev',0.975,'laby','robust distances','numlab',REW.outliers,'ylimy',ylimy);
title('Corrected reweighted MCD')
Total estimated time to complete MCD: 0.04 seconds
Input Arguments
Y — Data matrix containing n observations on v variables.
Rows of Y represent observations, and columns represent variables.
Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will be excluded from the computations.
Data Types: single| double
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'bdp',1/4
, 'bestr',10
, 'betathresh',false
, 'conflev',0.99
, 'conflevrew',0.99
, 'msg',1
, 'nocheck',1
, 'nsamp',10000
, 'refsteps',10
, 'refstepsbestr',10
, 'reftol',1e-8
, 'reftolbestr',1e-8
, 'restrfactor',100
, 'smallsamplecor',true
, 'modelT',5
, 'tolMCD',1e-20
, 'ysaveRAW',true
, 'ysaveREW',true
, 'plots',1
bdp
—Breakdown point.scalar.
(Number between 0 and 0.5). The default value is 0.5.
Example: 'bdp',1/4
Data Types: double
bestr
—Number of best solutions to store.scalar.
Number of "best locations" to remember from the subsamples. These will be later iterated until convergence (default=5)
Example: 'bestr',10
Data Types: double
betathresh
—Distribution to use.boolean.
If betathresh = true the distribution which is used to declare units as outliers is a mixture of Rocke scaled F distribution and Beta else (default) traditional chi^2 distribution is used.
Example: 'betathresh',false
Data Types: logical
conflev
—Confidence level.scalar.
Number between 0 and 1 containing confidence level which is used to declare units as outliers after reweighting.
Usually conflev=0.95, 0.975 0.99 (individual alpha) or 1-0.05/n, 1-0.025/n, 1-0.01/n (simultaneous alpha).
Default value is 0.975
Example: 'conflev',0.99
Data Types: double
conflevrew
—Confidence level for use for reweighting.scalar.
Number between 0 and 1 containing confidence level which is used to do the reweighting step. Default value is the one specified in previous option conflev.
Example: 'conflevrew',0.99
Data Types: double
msg
—Display or not messages on the screen.scalar.
If msg==1 (default) messages are displayed on the screen about estimated time to compute the final estimator else no message is displayed on the screen.
Example: 'msg',1
Data Types: double
nocheck
—No check on input data.scalar.
If nocheck is equal to 1 no check is performed on matrix Y. As default nocheck=0.
Example: 'nocheck',1
Data Types: double
nsamp
—Number of subsamples.scalar | matrix.
If nsamp is a scalar, it contains the number of subsamples of size v+1 which have to be extracted (if not given, default is nsamp=1000). If nsamp=0 all subsets will be extracted. If nsamp is a matrix it contains in the rows the indexes of the subsets which have to be extracted. nsamp in this case can be conveniently generated by function subsets.
Example: 'nsamp',10000
Data Types: double
refsteps
—Number of refining iterations.scalar.
Number of refining iterations in each subsample (default = 3).
refsteps = 0 means "raw-subsampling" without iterations.
Example: 'refsteps',10
Data Types: double
refstepsbestr
—Number of refining iterations.scalar.
Number of refining iterations for each best subset (default = 50).
Example: 'refstepsbestr',10
Data Types: double
reftol
—Refining steps tolerance.scalar.
Tolerance for the refining steps.
The default value is 1e-6;
Example: 'reftol',1e-8
Data Types: double
reftolbestr
—Tolerance for refining steps.scalar.
Value of tolerance for the refining steps for each of the best subsets.
The default value is 1e-8;
Example: 'reftolbestr',1e-8
Data Types: double
restrfactor
—Restriction factor.scalar.
Positive scalar greater or equal than 1 which constrains the allowed differences of the eigenvalues of the scatter matrix in each concentration step. The default value of restrfactor is Inf, that is no constraint is imposed on the eigenvalues of the covariace matrix in each subset.
Example: 'restrfactor',100
Data Types: double
smallsamplecor
—small sample correction factor.boolean.
Boolean which defines whether to use or not small sample correction factor to inflate the scale estimate. If it is equal to true the small sample correction factor is used. The default value of smallsamplecor is true, that is the correction is used.
Example: 'smallsamplecor',true
Data Types: logical
modelT
—controls how the consistency factor is applied to account
for the effect of trimming.scalar.
It is empty for the classic case when uncontaminated data are assumed to come from a normal distribution (default). If on the other hand the data are heavy-tailed and can be modelled by a Student-t distribution, modelT takes a positive value representing the degrees of freedom of the t-distribution;
if modelT is zero, then the degrees of freedom are estimated from the data (to be implemented).
Example: 'modelT',5
Data Types: double
tolMCD
—Tolerance to declare a subset as singular.scalar.
The default value of tolMCD is exp(-50*v).
Example: 'tolMCD',1e-20
Data Types: double
ysaveRAW
—save Y.boolean.
Boolean that is set to true to request that the data matrix Y is saved into the output structure RAW. This feature is meant at simplifying the use of function malindexplot.
Default is false, i.e. no saving is done.
Example: 'ysaveRAW',true
Data Types: logical
ysaveREW
—save Y.boolean.
Boolean that is set to true to request that the data matrix Y is saved into the output structure REW. This feature is meant at simplifying the use of function malindexplot.
Default is false, i.e. no saving is done.
Example: 'ysaveREW',true
Data Types: logical
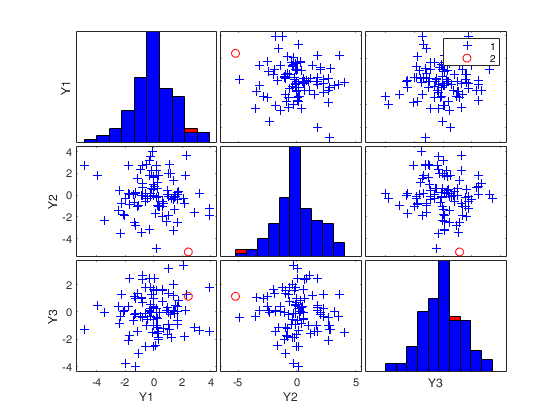
plots
—Plot on the screen.scalar | structure.
If plots is a structure or scalar equal to 1, generates: (1) two plots of Mahalanobis distances (raw and reweighted) against index number. The confidence level used to draw the confidence bands for the MD is given by the input option conflev. If conflev is not specified a nominal 0.975 confidence interval will be used.
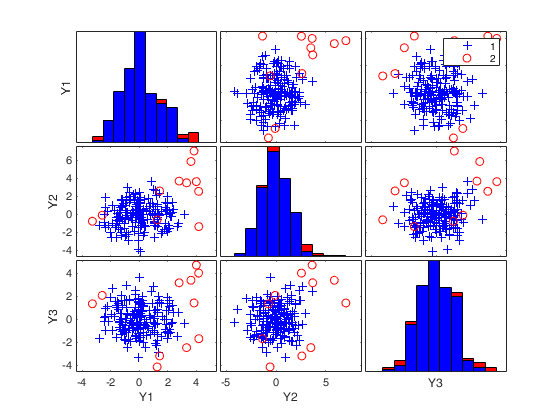
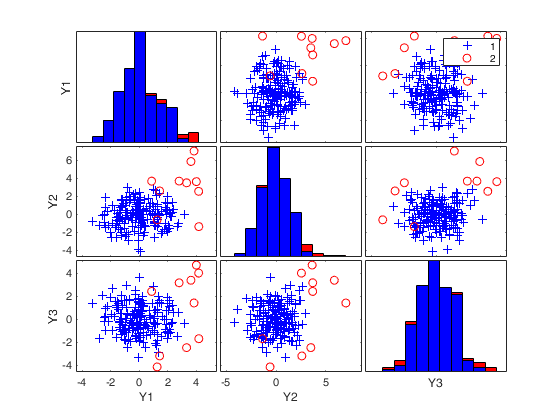
(2) two scatter plot matrices with the outliers (from raw and reweighted mcd estimators) highlighted.
If plots is a structure it may contain the following fields
| Value | Description |
|---|---|
labeladd |
if this option is '1', the outliers in the spm are labelled with their unit row index. The default value is labeladd='', i.e. no label is added. |
nameY |
cell array of strings containing the labels of the variables. As default value, the labels which are added are Y1, ...Yv. |
Example: 'plots',1
Data Types: double or structure
Output Arguments
RAW — description
Structure
Structure which contains the following fields
| Value | Description |
|---|---|
h |
scalar. The number of observations that have determined the MCD estimator |
loc |
1 x v vector containing raw MCD location of the data |
cov |
robust MCD estimate of covariance matrix. It is the raw MCD covariance matrix (multiplied by a finite sample correction factor and an asymptotic consistency factor). |
cor |
The raw MCD correlation matrix |
obj |
The determinant of the raw MCD covariance matrix. |
bs |
(v+1) x 1 vector containing the units forming best subset associated with MCD estimate of location. |
md |
n x 1 vector containing the estimates of the robust Mahalanobis distances (in squared units). This vector contains the distances of each observation from the raw MCD location of the data, relative to the raw MCD scatter matrix RAW.cov |
outliers |
A vector containing the list of the units declared as outliers using confidence level specified in input scalar conflev |
conflev |
Confidence level that was used to declare outliers |
singsub |
Number of subsets without full rank. Notice that out.singsub > 0.1*(number of subsamples) produces a warning |
weights |
n x 1 vector containing the estimates of the weights. Weights assume values 0 or 1. Weight is 1 if the associated observation has been used to compute centroid and covariance matrix. These weights determine which observations are used to compute the final MCD estimates. Unless there is a perfect fit sum(RAW.weights)=h |
plane |
In case of an exact fit, RAW.plane contains the coefficients of a (hyper)plane a_1(x_i1-m_1)+...+a_p(x_ip-m_p)=0 containing at least h observations, where (m_1,...,m_p) is the MCD location of these observations. This field is present only if there is exact fit. |
Y |
Data matrix Y. This field is present only if option ysaveRAW was set to 1. |
class |
'mcd' |
REW — description
Structure
Structure which contains the following fields:
| Value | Description |
|---|---|
loc |
The robust location of the data, obtained after reweighting, if the raw MCD is not singular. Otherwise the raw MCD center is given here. |
cov |
The robust covariance matrix, obtained after reweighting and multiplying with a finite sample correction factor and an asymptotic consistency factor, if the raw MCD is not singular. Otherwise the raw MCD covariance matrix is given here. |
cor |
The robust correlation matrix, obtained after reweighting |
md |
n x 1 vector containing the estimates of the robust Mahalanobis distances (in squared units). This vector contains the distances of each observation from the reweighted MCD location of the data, relative to the reweighted MCD scatter of the data These distances allow us to easily identify the outliers. If the reweighted MCD is singular, RAW.md is given here. |
outliers |
A vector containing the list of the units declared as outliers after reweighting. |
weights |
n x 1 vector containing the estimates of the weights. Weights assume values 0 or 1. Weight is 0 if the associated observation has been declared outlier. These weights determine which observations are used to compute the final MCD estimates. Remark: if the reweighted MCD is singular, RAW.weights is given here. |
method |
In case of an exact fit, REW.method contains a character string containing information about the method and about singular subsamples (if any). This field is present only if there is exact fit. |
plane |
In case of an exact fit, REW.plane contains the coefficients of a (hyper)plane a_1(x_i1-m_1)+...+a_p(x_ip-m_p)=0 containing at least h observations, where (m_1,...,m_p). This field is present only if there is exact fit. |
Y |
Data matrix Y. The field is present only if option ysaveREW was set to 1. |
class |
'mcdr'. |
varargout —Indices
of the subsamples extracted for
computing the estimate.
C : matrix of size nsamp-by-v
More About
Additional Details
MCD computes the MCD estimator of a multivariate data set. This estimator is given by the subset of h observations with smallest covariance determinant. The MCD location estimate is then the mean of those h points, and the MCD scatter estimate is their covariance matrix.
The default value of h is roughly 0.5n (where n is the total number of observations), but the user may choose each value between n/2 and n.
The MCD method is intended for continuous Gaussian variables, and assumes that the number of observations n is at least 5 times the number of variables p. If p is too large relative to n, it is better to use options betathresh=1 (that is to use a threshold based on beta distribution (for the units which determine the centroid and the covariance matrix) and F distribution (for the units which are excluded from the computation of centroid and covariance matrix) The MCD method was introduced in: Rousseeuw, P.J. (1984), Least Median of Squares Regression, "Journal of the American Statistical Association", Vol. 79, pp. 871-881.
The program below uses the technique of concentration steps described in Rousseeuw, P.J. and Van Driessen, K. (1999), "A Fast Algorithm for the Minimum Covariance Determinant Estimator," Technometrics, 41, pp. 212-223.
The MCD is a robust method in the sense that the estimates are not unduly influenced by outliers in the data, even if there are many outliers.
Due to the MCD's robustness, we can detect outliers by their large robust distances. The latter are defined like the usual Mahalanobis distance, but based on the MCD location estimate and scatter matrix (instead of the nonrobust sample mean and covariance matrix).
Remark: when more than h observations lie on a (hyper)plane, (perfect fit case) the program still yields the MCD location and scatter matrix, the latter being singular (as it should be), as well as the equation of the hyperplane.
About the modelT option. It applies a consistency factor derived for continuous Student-t data, to account for havy-tails distributions. The derivation of the factor is discussed by Barabesi et al. (2023), Trimming heavy-tailed multivariate data, submitted.
About the consistency factor. The consistency factor, which is applied to the scatter matrix to account for the effect of trimming observations, can be computed based on the nominal trimming percentage, which is , or based on the empirical one, which is h/n. The two values can slightly differ if n is small. By default, we use the nominal value. This means that the RAW residuals are based on the nominal value 1-bdp. On the other hand, note that currently the REW residuals are based on the empirical h/n to reflect the empirical nature of the reweighted approach.
References
Maronna, R.A., Martin D. and Yohai V.J. (2006), "Robust Statistics, Theory and Methods", Wiley, New York.
Acknowledgements
This function follows the lines of MATLAB/R code developed during the years by many authors. In particular, parts of the code rely on the LIBRA mcd implementation of Hubert and Verboven. For more details, see: https://wis.kuleuven.be/stat/robust/papers/2005/LIBRA.pdf and the R library Robustbase http://robustbase.r-forge.r-project.org/ The core of our routines, e.g. the resampling approach, however, has been completely redesigned, with considerable increase of the computational performance. Note that, for the moment, FSDA does not adopt the 'divide and conquer' partitioning method proposed by Rousseeuw and Van Driessen to speed up computations for large datasets. This partitioning method is applied in the R and LIBRA implementations of the mcd.
See Also

|
function-alpha.html |
function-cate.html |
 |
|
|
Functions |
|
• The developers of the toolbox • The forward search group • Terms of Use • Acknowledgments