PDrho
PDrho computes rho function for minimum density power divergence estimator
Syntax
rhoPD=PDrho(u,alpha)example
Examples
Related Examples
Input Arguments
Output Arguments
More About
References
Riani, M. Atkinson, A.C., Corbellini A. and Perrotta A. (2020), Robust Regression with Density Power Divergence: Theory, Comparisons and Data Analysis, Entropy, Vol. 22, 399.
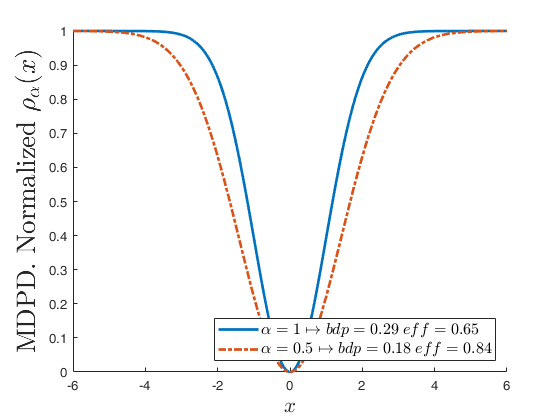
 Compare two rho functions for 2 different values of alpha.
Compare two rho functions for 2 different values of alpha.