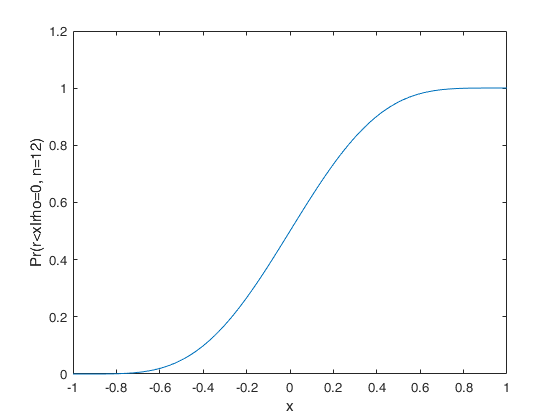
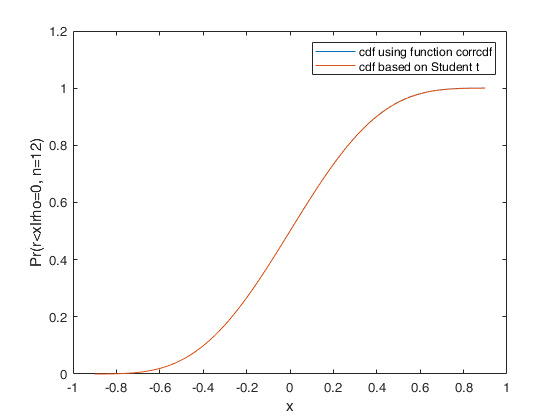
corrcdf
corrcdf computes correlation coefficient probability distribution function
Description
Examples
Related Examples
Input Arguments
Output Arguments
References
Das Gupta, S. (1980). Distribution of the Correlation Coefficient, in: Fienberg, S.E., Hinkley, D.V. (eds) R.A. Fisher: An Appreciation, Lecture Notes in Statistics, vol 1. Springer, New York, NY.
Acknowledgements
For additional information see https://mathworld.wolfram.com/CorrelationCoefficientBivariateNormalDistribution.html This function follows the lines of MATLAB code developed by Xu Cui, and the file exchange submission Joshua Carmichael (2022), sample correlation distribution function https://www.mathworks.com/matlabcentral/fileexchange/45785-sample-correlation-distribution-function/
 An example where x, rho and n are all scalars.
An example where x, rho and n are all scalars.