Vector with two elements associated with the center of the
ellipse
Data Types: single| double
Inverse of the
matrix of the quadratic form which defines the equation of the
ellipse. Sigma is interpretable as the covariance matrix of the
original data points.
Data Types: single| double
If conflev is a empty (default) the confidence level
which controls the size of the ellipse (c_{conflev}^2= is
computed as chi2inv(0.95,2). If the data are normally
distributed the ellipse covers 95 per cent of the
observations. If conflev is a scalar smaller than 1, the
confidence level $c_{conflev}^2$ is computed as
chi2inv(conflev,2). If conflev is a scalar greater or
equal than 1 no chi2inv is applied to conflev and
$c_{conflev}^2$=conflev.
Example: 'conflev', 0.99
Data Types: single | double
Line color, specified as an RGB triplet, a color
string, or 'none'. If you specify the Color as
'none', then the line is invisible.
An RGB triplet is a three-element row vector whose
elements specify the intensities of the red,
green, and blue components of the color. The
intensities must be in the range [0,1], for
example, [0.4 0.6 0.7].
Example: 'Color', 'r'
Data Types: [0 0 1] (default) | RGB triplet | color string | 'none'
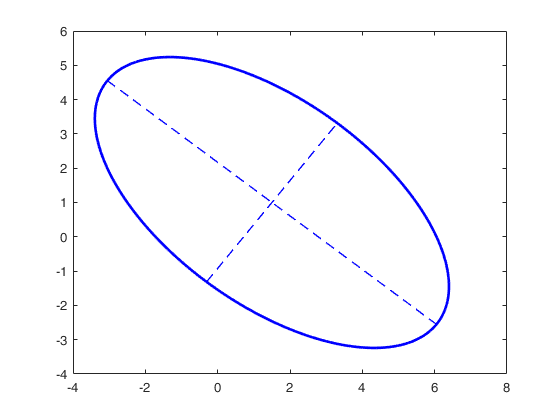
If axes is true (default)
dottted lines along the major axes of the ellipse are
drawn else just the ellipse contour appears.
Example: 'axesellipse', false
Data Types: Boolean
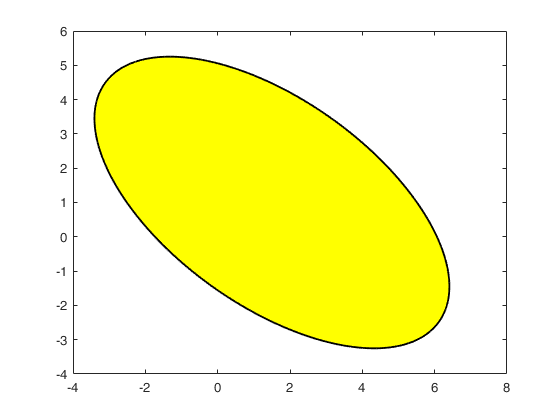
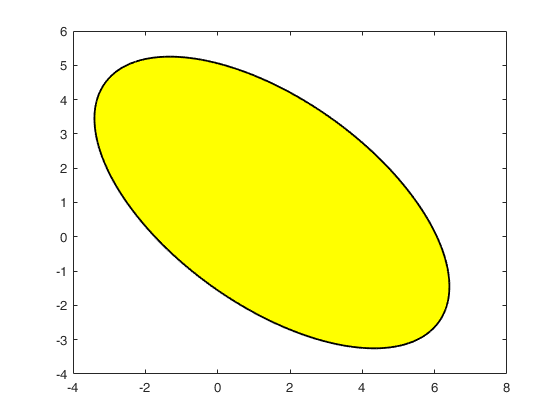
 Draw the ellipse using a blue color line.
Draw the ellipse using a blue color line.