exactcdf
exactcdf finds exact p-values
Description
Function for finding the exact cdf of each element in the vector x with respect to the empirical distribution, represented by the vector empdist, i.e. the generic element i of the output vector p is the result of: where I is the indicator function and K is the length of vector empdist
Examples
Related Examples
Input Arguments
Output Arguments
References
Athey, S., Eckles, D., & Imbens, G. W. (2018). Exact p-values for network interference, "Journal of the American Statistical Association", Vol. 113, pp. 230-240.
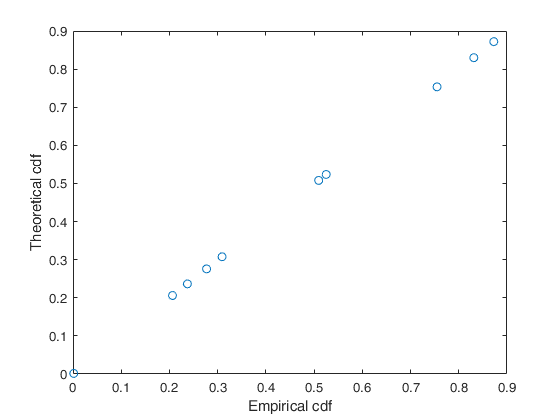
 exactcdf with two input arguments.
exactcdf with two input arguments.