pcaFS
pcaFS performs Principal Component Analysis (PCA) on raw data.
Description
The main differences with respect to MATLAB function pca are: 1) accepts an input X also as table;
2) produces in table format the percentage of the variance explained single and cumulative of the various components and the associated scree plot, in order to decide about the number of components to retain.
3) returns the loadings in table format and shows them graphically.
4) provides guidelines about the automatic choice of the number of components;
5) returns the communalities for each variable with respect to the first k principal components in table format;
6) returns the orthogonal distance ($OD_i$) of each observation to the PCA subspace. For example, if the subspace is defined by the first two principal components, $OD_i$ is computed as:
\[ OD_i=|| z_i- V_{(2)} V_{(2)}' z_i || \]where z_i is the i-th row of the original centered data matrix $Z$ of dimension $n \times v$ and $V_{(2)}=(v_1 v_2)$ is the matrix of size $p \times 2$ containing the first two eigenvectors of $Z'Z/(n-1)$. The observations with large $OD_i$ are not well represented in the space of the principal components.
7) returns the score distance $SD_i$ of each observation. For example, if the subspace is defined by the first two principal components, $SD_i$ is computed as:
\[ SD_i=\sqrt{(z_i'v_1)^2/l_1+ (z_i'v_2)^2/l_2 } \]where $l_1$ and $l_2$ are the first two eigenvalues of $Z'Z/(n-1)$.
8) calls app biplotFS which enables to obtain an interactive biplot in which points, row labels or arrows can be shown or hidden. This app also gives the possibility of controlling the length of the arrows and the position of the row points through two interactive slider bars. In the app it is also possible to color row points depending on the orthogonal distance ($OD_i$) of each observation to the PCA subspace. If optional input argument bsb or bdp is specified, it is possible to have in the app two tabs which enable the user to select the breakdown point of the analysis or the subset size to use in the svd. The units which are declared as outliers or the units outside the subset are shown in the biplot with filled circles.
Use of pcaFS on the ingredients dataset.out
=pcaFS(Y,
Name, Value)
Examples
Use of pcaFS with citiesItaly dataset.
load citiesItaly; % Use all default options out=pcaFS(citiesItaly);
 Use of pcaFS on the ingredients dataset.
Use of pcaFS on the ingredients dataset.
 Use of pcaFS on the ingredients dataset.
Use of pcaFS on the ingredients dataset.
load hald % Operate on the covariance matrix. out=pcaFS(ingredients,'standardize',false,'biplot',0);
The first PC already explains more than 0.95^v variability
In what follows we still extract the first 2 PCs
Initial covariance matrix
Y1 Y2 Y3 Y4
_____ _____ _____ _____
Y1 1.00 0.23 -0.82 -0.25
Y2 0.23 1.00 -0.14 -0.97
Y3 -0.82 -0.14 1.00 0.03
Y4 -0.25 -0.97 0.03 1.00
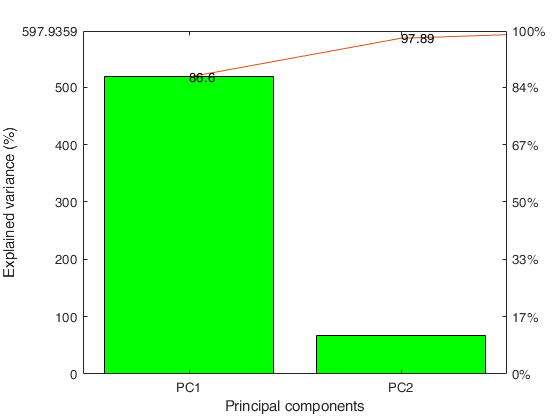
Explained variance by PCs
Eigenvalues Explained_Variance Explained_Variance_cum
___________ __________________ ______________________
PC1 517.80 86.60 86.60
PC2 67.50 11.29 97.89
PC3 12.41 2.07 99.96
PC4 0.24 0.04 100.00
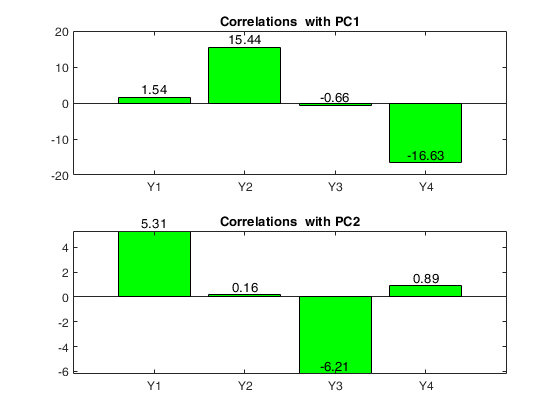
Loadings = correlations between variables and PCs
PC1 PC2
______ _____
Y1 1.54 5.31
Y2 15.44 0.16
Y3 -0.66 -6.21
Y4 -16.63 0.89
Communalities
PC1 PC2 PC1-PC2
______ _____ _______
Y1 2.38 28.17 30.55
Y2 238.39 0.03 238.41
Y3 0.44 38.51 38.94
Y4 276.60 0.79 277.39
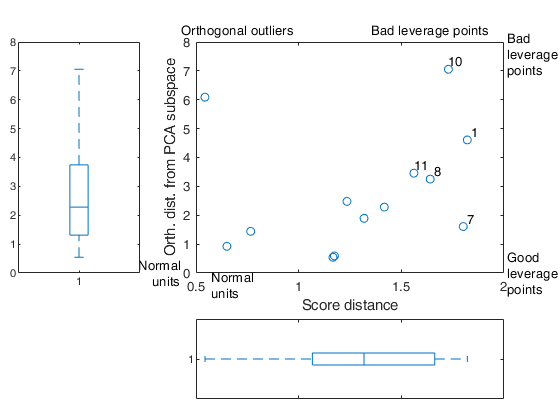
Units with the 5 largest values of (combined) score and orthogonal distance
10 1 7 8 11
Related Examples
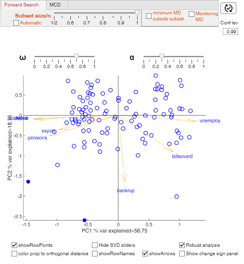
 Use of pcaFS with option robust true.
Use of pcaFS with option robust true.
 Use of pcaFS with option robust true.
Use of pcaFS with option robust true.
load citiesItaly; % Use all default options out=pcaFS(citiesItaly,'robust',true);
Initial correlation matrix
addedval depos pensions unemploy export bankrup billsoverd
________ _____ ________ ________ ______ _______ __________
addedval 1.00 0.91 0.73 -0.82 0.59 -0.04 -0.49
depos 0.91 1.00 0.70 -0.79 0.53 -0.03 -0.49
pensions 0.73 0.70 1.00 -0.52 0.35 0.24 -0.46
unemploy -0.82 -0.79 -0.52 1.00 -0.61 0.18 0.43
export 0.59 0.53 0.35 -0.61 1.00 0.07 -0.21
bankrup -0.04 -0.03 0.24 0.18 0.07 1.00 0.38
billsoverd -0.49 -0.49 -0.46 0.43 -0.21 0.38 1.00
Explained variance by PCs
Eigenvalues Explained_Variance Explained_Variance_cum
___________ __________________ ______________________
PC1 3.97 56.75 56.75
PC2 1.31 18.76 75.51
PC3 0.80 11.45 86.97
PC4 0.45 6.36 93.32
PC5 0.22 3.10 96.42
PC6 0.17 2.43 98.85
PC7 0.08 1.15 100.00
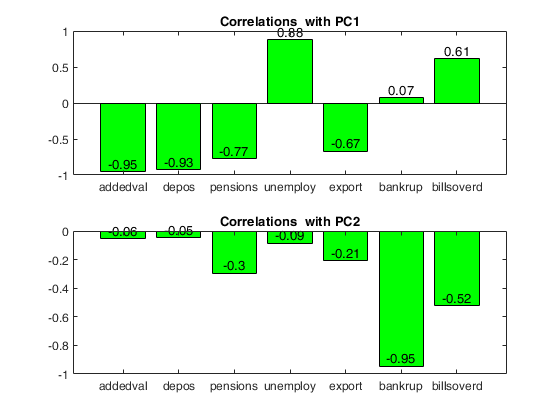
Loadings = correlations between variables and PCs
PC1 PC2
_____ _____
addedval -0.95 -0.06
depos -0.93 -0.05
pensions -0.77 -0.30
unemploy 0.88 -0.09
export -0.67 -0.21
bankrup 0.07 -0.95
billsoverd 0.61 -0.52
Communalities
PC1 PC2 PC1-PC2
____ ____ _______
addedval 0.91 0.00 0.91
depos 0.86 0.00 0.87
pensions 0.60 0.09 0.69
unemploy 0.77 0.01 0.78
export 0.45 0.04 0.49
bankrup 0.01 0.89 0.90
billsoverd 0.38 0.27 0.65
Units with the 5 largest values of (combined) score and orthogonal distance
65 17 70 99 76


 Use of pcaFS with options Latitude and Longitude.
Use of pcaFS with options Latitude and Longitude.
 Use of pcaFS with options Latitude and Longitude.
Use of pcaFS with options Latitude and Longitude.
load citiesItaly2024.mat
X=citiesItaly2024;
% Retrieve Latitude and Longitude of each province
LatLong=X.Properties.UserData{2};
Latitude=LatLong(:,1);
Longitude=LatLong(:,2);
out=pcaFS(X,'Latitude',Latitude,'Longitude',Longitude);The first PC already explains more than 0.95^v variability
In what follows we still extract the first 2 PCs
Initial correlation matrix
Deposit Bankrup UrbanFra Paym30D ElecPar QualLif Protest SalaryA SpendingA Employm AddedVa LowISEE
_______ _______ ________ _______ _______ _______ _______ _______ _________ _______ _______ _______
Deposit 1.00 -0.33 -0.70 0.72 0.58 0.76 -0.14 0.74 0.75 0.79 0.79 -0.76
Bankrup -0.33 1.00 0.26 -0.39 -0.13 -0.44 0.33 -0.18 -0.22 -0.32 -0.24 0.40
UrbanFra -0.70 0.26 1.00 -0.77 -0.74 -0.74 0.23 -0.74 -0.81 -0.90 -0.70 0.83
Paym30D 0.72 -0.39 -0.77 1.00 0.69 0.81 -0.35 0.74 0.79 0.80 0.63 -0.82
ElecPar 0.58 -0.13 -0.74 0.69 1.00 0.58 -0.16 0.64 0.78 0.73 0.55 -0.62
QualLif 0.76 -0.44 -0.74 0.81 0.58 1.00 -0.37 0.70 0.77 0.83 0.72 -0.86
Protest -0.14 0.33 0.23 -0.35 -0.16 -0.37 1.00 -0.14 -0.31 -0.31 -0.11 0.39
SalaryA 0.74 -0.18 -0.74 0.74 0.64 0.70 -0.14 1.00 0.85 0.80 0.86 -0.66
SpendingA 0.75 -0.22 -0.81 0.79 0.78 0.77 -0.31 0.85 1.00 0.92 0.78 -0.79
Employm 0.79 -0.32 -0.90 0.80 0.73 0.83 -0.31 0.80 0.92 1.00 0.81 -0.86
AddedVa 0.79 -0.24 -0.70 0.63 0.55 0.72 -0.11 0.86 0.78 0.81 1.00 -0.68
LowISEE -0.76 0.40 0.83 -0.82 -0.62 -0.86 0.39 -0.66 -0.79 -0.86 -0.68 1.00
Explained variance by PCs
Eigenvalues Explained_Variance Explained_Variance_cum
___________ __________________ ______________________
PC 1 8.02 66.82 66.82
PC 2 1.29 10.77 77.60
PC 3 0.77 6.45 84.05
PC 4 0.52 4.37 88.42
PC 5 0.36 3.00 91.42
PC 6 0.27 2.24 93.66
PC 7 0.24 1.98 95.64
PC 8 0.17 1.44 97.08
PC 9 0.13 1.04 98.12
PC10 0.10 0.82 98.94
PC11 0.09 0.73 99.66
PC12 0.04 0.34 100.00
Loadings = correlations between variables and PCs
PC1 PC2
_____ _____
Deposit -0.86 -0.10
Bankrup 0.38 -0.69
UrbanFra 0.89 0.10
Paym30D -0.89 0.11
ElecPar -0.77 -0.22
QualLif -0.89 0.18
Protest 0.34 -0.73
SalaryA -0.86 -0.27
SpendingA -0.93 -0.12
Employm -0.96 -0.04
AddedVa -0.84 -0.24
LowISEE 0.90 -0.17
Communalities
PC1 PC2 PC1-PC2
____ ____ _______
Deposit 0.73 0.01 0.74
Bankrup 0.15 0.47 0.62
UrbanFra 0.80 0.01 0.81
Paym30D 0.79 0.01 0.80
ElecPar 0.59 0.05 0.64
QualLif 0.80 0.03 0.83
Protest 0.11 0.53 0.65
SalaryA 0.74 0.07 0.82
SpendingA 0.86 0.01 0.88
Employm 0.91 0.00 0.92
AddedVa 0.71 0.06 0.76
LowISEE 0.82 0.03 0.85
Units with the 5 largest values of (combined) score and orthogonal distance
15 21 89 58 60





 Use of pcaFS with option ShapeFile.
Use of pcaFS with option ShapeFile.
 Use of pcaFS with option ShapeFile.
Use of pcaFS with option ShapeFile.Note that this option requires the Mapping Toolbox to be installed.
a=struct2table(ver);
MappingInstalled=any(string(a{:,1})=="Mapping Toolbox");
if MappingInstalled ==true
load citiesItaly2024.mat
X=citiesItaly2024;
ShapeFile=X.Properties.UserData{1};
out=pcaFS(X,"ShapeFile",ShapeFile,'biplot',0);
else
disp('This option requires that the "mapping toolbox" is installed')
endThe first PC already explains more than 0.95^v variability
In what follows we still extract the first 2 PCs
Initial correlation matrix
Deposit Bankrup UrbanFra Paym30D ElecPar QualLif Protest SalaryA SpendingA Employm AddedVa LowISEE
_______ _______ ________ _______ _______ _______ _______ _______ _________ _______ _______ _______
Deposit 1.00 -0.33 -0.70 0.72 0.58 0.76 -0.14 0.74 0.75 0.79 0.79 -0.76
Bankrup -0.33 1.00 0.26 -0.39 -0.13 -0.44 0.33 -0.18 -0.22 -0.32 -0.24 0.40
UrbanFra -0.70 0.26 1.00 -0.77 -0.74 -0.74 0.23 -0.74 -0.81 -0.90 -0.70 0.83
Paym30D 0.72 -0.39 -0.77 1.00 0.69 0.81 -0.35 0.74 0.79 0.80 0.63 -0.82
ElecPar 0.58 -0.13 -0.74 0.69 1.00 0.58 -0.16 0.64 0.78 0.73 0.55 -0.62
QualLif 0.76 -0.44 -0.74 0.81 0.58 1.00 -0.37 0.70 0.77 0.83 0.72 -0.86
Protest -0.14 0.33 0.23 -0.35 -0.16 -0.37 1.00 -0.14 -0.31 -0.31 -0.11 0.39
SalaryA 0.74 -0.18 -0.74 0.74 0.64 0.70 -0.14 1.00 0.85 0.80 0.86 -0.66
SpendingA 0.75 -0.22 -0.81 0.79 0.78 0.77 -0.31 0.85 1.00 0.92 0.78 -0.79
Employm 0.79 -0.32 -0.90 0.80 0.73 0.83 -0.31 0.80 0.92 1.00 0.81 -0.86
AddedVa 0.79 -0.24 -0.70 0.63 0.55 0.72 -0.11 0.86 0.78 0.81 1.00 -0.68
LowISEE -0.76 0.40 0.83 -0.82 -0.62 -0.86 0.39 -0.66 -0.79 -0.86 -0.68 1.00
Explained variance by PCs
Eigenvalues Explained_Variance Explained_Variance_cum
___________ __________________ ______________________
PC 1 8.02 66.82 66.82
PC 2 1.29 10.77 77.60
PC 3 0.77 6.45 84.05
PC 4 0.52 4.37 88.42
PC 5 0.36 3.00 91.42
PC 6 0.27 2.24 93.66
PC 7 0.24 1.98 95.64
PC 8 0.17 1.44 97.08
PC 9 0.13 1.04 98.12
PC10 0.10 0.82 98.94
PC11 0.09 0.73 99.66
PC12 0.04 0.34 100.00
Loadings = correlations between variables and PCs
PC1 PC2
_____ _____
Deposit -0.86 -0.10
Bankrup 0.38 -0.69
UrbanFra 0.89 0.10
Paym30D -0.89 0.11
ElecPar -0.77 -0.22
QualLif -0.89 0.18
Protest 0.34 -0.73
SalaryA -0.86 -0.27
SpendingA -0.93 -0.12
Employm -0.96 -0.04
AddedVa -0.84 -0.24
LowISEE 0.90 -0.17
Communalities
PC1 PC2 PC1-PC2
____ ____ _______
Deposit 0.73 0.01 0.74
Bankrup 0.15 0.47 0.62
UrbanFra 0.80 0.01 0.81
Paym30D 0.79 0.01 0.80
ElecPar 0.59 0.05 0.64
QualLif 0.80 0.03 0.83
Protest 0.11 0.53 0.65
SalaryA 0.74 0.07 0.82
SpendingA 0.86 0.01 0.88
Employm 0.91 0.00 0.92
AddedVa 0.71 0.06 0.76
LowISEE 0.82 0.03 0.85
Units with the 5 largest values of (combined) score and orthogonal distance
15 21 89 58 60




Input Arguments
Y — Input data.
2D array or table.
n x p data matrix; n observations and p variables. Rows of Y represent observations, and columns represent variables.
Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.
Data Types: single|double
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'biplot',0
, 'dispresults',false
, 'Latitude',[54 43.2 ... 47]
, 'Longitude',[54 43.2 ... 47]
, 'NumComponents',2
, 'plots',0
, 'bsb',[2 10:90 93]
, 'ShapeFile','shapefileName'
, 'smartEVchart',true
, 'standardize',false
biplot
—launch app biplotFS.scalar.
If biplot is 1 (default) app biplotFS is automatically launched. With this app it is possible to show in a dynamic way the rows points (PC coordinates), the arrows, the row labels and control with a scrolling bar the length of the arrows and the spread of row points.
Example: 'biplot',0
Data Types: double
dispresults
—show the results in the command window.boolean.
If dispresults is true, the percentage of variance explained together with the loadings, the criteria for deciding the number of components to retain and the 5 units with the largest score and orthogonal distance (combined) are shown in the command window.
Example: 'dispresults',false
Data Types: char
Latitude
—Latitude coordinates in degrees of the rows.nx1 vector containing the numerical values of latitudes for each row.
If vectors Latitude and Longitude are present once brushing of the units in biplotAPP is done, the geobubble of the brushed units automatically appears. The size of the bubble is proportional to the value of the first principal component while the color of the bubbles depends on the value of the second principal component.
Example: 'Latitude',[54 43.2 ... 47]
Data Types: vector with elements in the range [–90, 90]
Longitude
—Longitude coordinates in degrees of the rows.nx1 vector containint the numerical values of latitudes for each row.
If vectors Latitude and Longitude are present once brushing of the units in biplotAPP is done, the geobubble of the brushed units automatically appears. The size of the bubble is proportional to the value of the first principal component while the color of the bubbles depends on the value of the second principal component.
Example: 'Longitude',[54 43.2 ... 47]
Data Types: vector with elements in the range [–90, 90]
NumComponents
—the number of components desired.specified as a scalar integer $k$ satisfying $0 < k \leq p$.
When specified, pcaFS returns the first $k$ columns of out.coeff and out.score. If NumComponents is not specified pcaFS returns the minimum number of components which cumulatively enable to explain a percentage of variance which is equal at least to $0.95^p$. If this threshold is exceeded already by the first PC, pcaFS still returns the first two PCs.
Example: 'NumComponents',2
Data Types: single|double
plots
—plots on the screen.scalar.
If plots is 1 (default) it is possible to show on the screen the scree plot of the variance explained, the plot of the loadings for the first two PCs.
Example: 'plots',0
Data Types: double
robust
—robust principal components.boolean | struct.
If robust is a scalar boolean equal to true (default), FS is applied and using a Bonferronized confidence level units are declared as outliers. If robust is a struct it is possible to choose between FS or MCD and the structure may contain the following fields:
| Value | Description |
|---|---|
bsb |
units forming subset on which to compute the svd. bsb can be either a numeric vector of length m (m<=n) containing the list of the units (e.g. 1:50) or a logical vector of length n containing the true for the units which have to be used in the calculation of svd. For example bsb=true(n,1), bsb(13)=false; excludes from the svd unit number 13. The other units are projected into this robust space. Note that is robust.bsb is supplied all the other options are ignored. |
conflev |
scalar in the interval (0 1) which contains the confidence level to declare the units as outliers. if robust.conflev is not specified or if it is missing a 0.99 Bonferronized confidence level is used. |
class |
class can be either 'FS' (default) or 'MCD' or 'MM' in order to choose between Forward search, or minimum covariance determinant or MM estimators. |
bdp |
break down point to use in the 'FS' or 'MCD' estimator or in the preliminary S estimator which is used to compute the MM. The default is bdp=0.4; It measures the fraction of outliers the algorithm should resist. In this case any value greater than 0 but smaller or equal than 0.5 will do fine. |
eff |
nominal efficiency to use for the MM estimator (note that this field is used just if robust.class is 'MM') |
Example: 'bsb',[2 10:90 93]
Data Types: double or logical
ShapeFile
—name of ShapeFile or geospatial table containing shapes.character | string | geotable.
Name of the ShapeFile containing the containing the geometric details of the rows. The ShapeFile, which is loaded using function readgeotable, must have n rows and the n rows must have the same order of the n rows of Y. The default value of shapefile is empty that is we assume that no shapefile is given. If ShapeFile is given an additional GUI containing the areas colored using the first PC is shown. If this file is given in the biplot once a particular area is selected the map showing the shape of the associated points is shown automatically on the screen (for more information see the release notes of FSDA 2025b).
Remark: note that this option can be used just is the "Mapping toolbox" is installed.
Example: 'ShapeFile','shapefileName'
Data Types: char or string or geotable
smartEVchart
—Eigenvectors shown as ordered-bar and line plots.boolean.
This plot facilitates the interpretation of the components.
If smartEVchart is true (default is false), a new plot is shown for each component.
In the upper panel, we show the bars associated with the eigenvector elements, sorted by magnitude. Bars are displayed in blue or red depending on their sign.
In the bottom panel, we show the coefficients arranged along a line. The vertical labels have a magnitude proportional to the importance of the corresponding coefficient. Finally, the caption of the plot displays the equation of the corresponding component as a linear combination of the original (scaled) variables.
Example: 'smartEVchart',true
Data Types: boolean
standardize
—standardize data.boolean.
Boolean which specifies whether to standardize the variables, that is we operate on the correlation matrix (default) or simply remove column means (in this last case we operate on the covariance matrix).
Example: 'standardize',false
Data Types: boolean
Output Arguments
out — description
Structure
Structure which contains the following fields
| Value | Description |
|---|---|
Rtable |
p-by-p correlation matrix in table format. |
class |
character vector containing pcaFS. |
explained |
p \times 3 matrix containing respectively 1st col = eigenvalues; 2nd col = Explained Variance (in percentage) 3rd col = Cumulative Explained Variance (in percentage) |
explainedT |
the same as out.explained but in table format. |
coeff |
p-by-NumComponents matrix containing the ordered eigenvectors of the correlation (covariance matrix) in table format. First column is referred to first eigenvector ... Note that out.coeff'*out.coeff= I_NumComponents. |
coeffT |
the same as out.coeff but in table format. |
loadings |
p-by-NumComponents matrix containing the correlation coefficients between the original variables and the first NumComponents principal components. |
loadingsT |
the same as out.loadings but in table format. |
score |
the principal component scores. The rows of out.score correspond to observations, columns to components. The covariance matrix of out.score is $\Lambda$ (the diagonal matrix containing the eigenvalues of the correlation (covariance matrix). |
scoreT |
the same as outscore but in table format. |
communalities |
matrix with p-by-2*NumComponents-1 columns. The first NumComponents columns contain the communalities (variance extracted) by the the first NumComponents principal components. Column NumComponents+1 contains the communalities extracted by the first two principal components. Column NumComponents+2 contains the communalities extracted by the first three principal components... |
communalitiesT |
the same as out.communalities but in table format. |
orthDist |
orthogonal distance from PCA subspace. Column vector of length n containing the orthogonal distance of each observation from the PCA subspace. |
scoreDist |
score distance from centroid. Column vector of length n containing the score distance of each observation from the PCA subspace. The analysis of out.orthDist and out.scoreDist reveals the good leverage points, the orthogonal outliers and the bad leverage points. Good leverage points: points which lie close to the PCA space but far from the regular observations. Good leverage points have a large score distance and low orthogonal distance. Orthogonal outliers are points which have a large orthogonal distance to the PCA subspace but cannot be seen when we look only at their projection on the PCA subspace. Bad leverage points are points which have a large orthogonal distance and whose projection on the PCA subspace is remote from the typical projections. These points have a large score distance and a large orthogonal distance. |