FE_int_vol_Fejer
FE_int_vol_Fejer computes the integrated variance from a diffusion process via the Fourier estimator using Fejer kernel
Description
FE_int_vol_Fejer computes the integrated variance of univariate timeseries data from a diffusion process by the Fourier estimator with Fejer kernel
FE_int_vol_Fejer called with optional input argument N.ivar
=FE_int_vol_Fejer(x,
t,
Name, Value)
Examples
Input Arguments
Output Arguments
More About
References
Mancino, M.E., Recchioni, M.C., Sanfelici, S. (2017), Fourier-Malliavin Volatility Estimation. Theory and Practice, "Springer Briefs in Quantitative Finance", Springer.
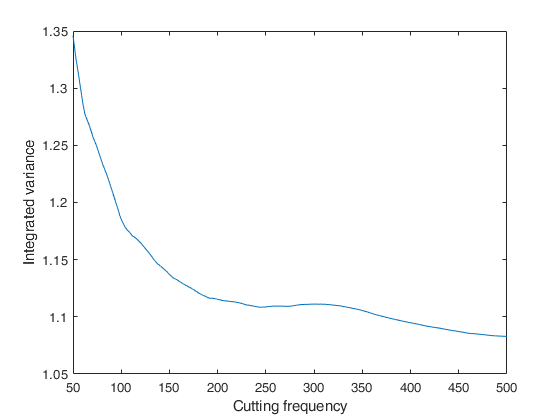
 Example of call of FE_int_vol_Fejer with just two input arguments.
Example of call of FE_int_vol_Fejer with just two input arguments.