FSRBeda

FSRBeda enables to monitor several quantities in each step of the Bayesian search

expand all in page

Syntax

Description

example

out =FSRBeda(y, X) FSRBeda with all default options.

example

out =FSRBeda(y, X, Name, Value) FSRBeda with optional arguments.

Examples

expand all

  • FSRBeda with all default options.

    • Common part to all examples: load Houses Price Dataset. 

    load hprice.txt;
% setup parameters
n=size(hprice,1);
y=hprice(:,1);
X=hprice(:,2:5);
[out]=FSRBeda(y,X);

  • FSRBeda with optional arguments.

    • load hprice.txt;
% setup parameters
n=size(hprice,1);
y=hprice(:,1);
X=hprice(:,2:5);
bayes=struct;
n0=5;
bayes.n0=n0;
% set \beta components
beta0=0*ones(5,1);
beta0(2,1)=10;
beta0(3,1)=5000;
beta0(4,1)=10000;
beta0(5,1)=10000;
bayes.beta0=beta0;
% \tau
s02=1/4.0e-8;
tau0=1/s02;
bayes.tau0=tau0;
% R prior settings
R=2.4*eye(5);
R(2,2)=6e-7;
R(3,3)=.15;
R(4,4)=.6;
R(5,5)=.6;
R=inv(R);
bayes.R=R;
[out]=FSRBeda(y,X,'bayes',bayes);

    Related Examples

    expand all

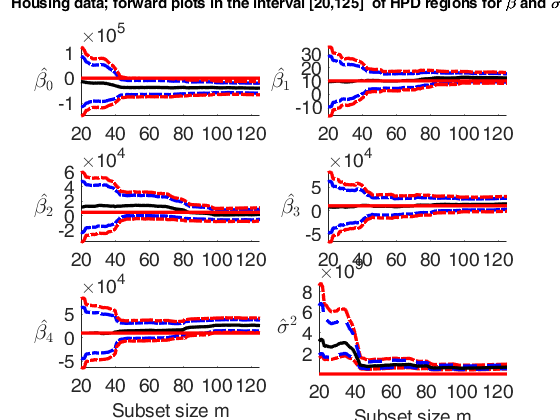
  • Plot posterior estimates of beta and sigma2.

    • Plot posterior estimates of beta and sigma2 in the interval (subset size) [20 125]. 

    % In this example for the house price data we monitor the forward plots
% of the parameters of the linear model adding 95% and 99% HPD
% regions. The first 8 panels refer to the elements of $\beta_1$
% and the bottom right-hand panel refer to the estimate of sigma2.
% The horizontal lines correspond to prior values    
% The vertical lines refer to the step prior to the introduction of the first outlier
% init = point to start monitoring diagnostics along the FS
% run routine FSRB in order to find the outliers automatically
load hprice.txt;
% setup parameters
n=size(hprice,1);
y=hprice(:,1);
X=hprice(:,2:5);
bayes=struct;
n0=5;
bayes.n0=n0;
% set \beta components
beta0=0*ones(5,1);
beta0(2,1)=10;
beta0(3,1)=5000;
beta0(4,1)=10000;
beta0(5,1)=10000;
bayes.beta0=beta0;
% \tau
s02=1/4.0e-8;
tau0=1/s02;
bayes.tau0=tau0;
% R prior settings
R=2.4*eye(5);
R(2,2)=6e-7;
R(3,3)=.15;
R(4,4)=.6;
R(5,5)=.6;
R=inv(R);
bayes.R=R;       
outBA=FSRB(y,X,'bayes',bayes', 'plots',0);
dout=n-length(outBA.ListOut);
% init = initial point to start monitoring
init=20;
xlimL=init; % lower value of xlim
xlimU=125;  % upper value of xlim 
outBAeda=FSRBeda(y,X,'bayes',bayes,'init',init, 'conflev', [0.95 0.99]);
% Set font size, line width and line style
figure;
lwd=2.5;
FontSize=14;
linst={'-','--',':','-.','--',':'};
for j=1:5
my_subplot=subplot(3,2,j);
hold('on')
% plot 95% and 99% HPD  trajectories
plot(outBAeda.beta1(:,1),outBAeda.beta1HPD(:,1:2,j),'LineStyle',linst{4},'LineWidth',lwd,'Color','b')
plot(outBAeda.beta1(:,1),outBAeda.beta1HPD(:,3:4,j),'LineStyle',linst{4},'LineWidth',lwd,'Color','r')
% plot posterior estimate of beta1_j
plot(outBAeda.beta1(:,1),outBAeda.beta1(:,j+1)','LineStyle',linst{1},'LineWidth',lwd,'Color','k')
% Add the horizontal line which corresponds to prior values
xL = get(my_subplot,'XLim');
line(xL,[beta0(j) beta0(j)],'Color','r','LineWidth',lwd);
% Set ylim
ylimU=max([outBAeda.beta1HPD(:,4,j); beta0(j)]);
ylimL=min([outBAeda.beta1HPD(:,3,j); beta0(j)]);
ylim([ylimL ylimU])
% Add vertical line in correspondence of the step prior to the
% entry of the first outlier
line([dout; dout],[ylimL; ylimU],'Color','r','LineWidth',lwd);
% Set xlim
xlim([xlimL xlimU]);
ylabel(['$\hat{\beta_' num2str(j-1) '}$'],'Interpreter','LaTeX','FontSize',20,'rot',-360);
set(gca,'FontSize',FontSize);
if j>4
xlabel('Subset size m','FontSize',FontSize);
end
end
% Subplot associated with the monitoring of sigma^2
subplot(3,2,6);
%figure()
hold('on')
% 99%
plot(outBAeda.sigma21HPD(:,1),outBAeda.sigma21HPD(:,4:5),'LineStyle',linst{4},'LineWidth',lwd,'Color','r')
% 95%
plot(outBAeda.sigma21HPD(:,1),outBAeda.sigma21HPD(:,2:3),'LineStyle',linst{2},'LineWidth',lwd,'Color','b')
% Plot 1\/tau1
plot(outBAeda.S21(:,1),1./outBAeda.S21(:,3),'LineWidth',lwd,'Color','k')
ylabel('$\hat{\sigma}^2$','Interpreter','LaTeX','FontSize',20,'rot',-360);
set(gca,'FontSize',FontSize);
% Set ylim
ylimU=max([outBAeda.sigma21HPD(:,5); s02]);
ylimL=min([outBAeda.sigma21HPD(:,4); s02]);
ylim([ylimL ylimU])
% Set xlim
xlim([xlimL xlimU]);
xL = get(my_subplot,'XLim');
% Add the horizontal line which corresponds to prior value of $\sigma^2$
line(xL,[s02 s02],'Color','r','LineWidth',lwd);
% Add vertical line in correspondence of the step prior to the
% entry of the first outlier
line([dout; dout],[ylimL; ylimU],'Color','r','LineWidth',lwd);
xlabel('Subset size m','FontSize',FontSize);
% Add multiple title
suplabel(['Housing data; forward plots in the interval ['...
num2str(xlimL) ',' num2str(xlimU) ...
']  of HPD regions for \beta and \sigma^2'],'t');
    Observed curve of r_min is at least 10 times greater than 99.99% envelope
--------------------------------------------------
-------------------------
Signal detection loop
Tentative signal in central part of the search: step m=511 because
rmin(511,546)>99.99% and rmin(510,546)>99.99% and rmin(512,546)>99.99%
rmin(511,546)>99.999%

-------------------
Signal validation exceedance of upper envelopes
Validated signal
-------------------------------
Start resuperimposing envelopes from step m=510
Superimposition stopped because r_{min}(512,529)>99.9% envelope
Subsample of 528 units is homogeneous
----------------------------
Final output
Number of units declared as outliers=18
Summary of the exceedances
           1          99         999        9999       99999
          10          64          48          38          29

m=100
m=200
m=300
m=400
m=500
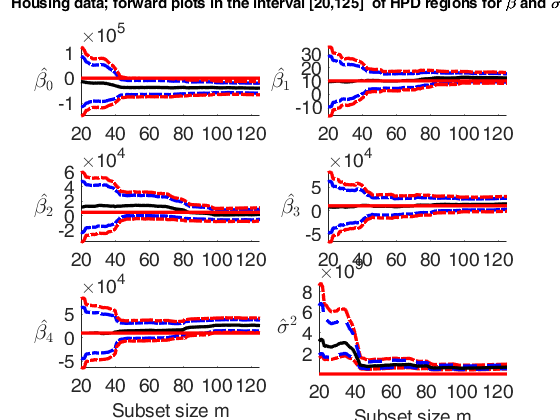
    Click here for the graphical output of this example (link to Ro.S.A. website)

  • Plot posterior estimates of beta and sigma2 in the last steps.

    • Plot posterior estimates of beta and sigma2 in the interval (subset size) [250 n+1]. 

    % In this example for the house price data we monitor the forward plots
% of the parameters of the linear model adding 95% and 99% HPD
% regions. The first 8 panels refer to the elements of $\beta_1$
% and the bottom right-hand panel refer to the estimate of sigma2.
% The horizontal lines correspond to prior values    
% The vertical lines refer to the step prior to the introduction of the first outlier
% init = point to start monitoring diagnostics along the FS
% run routine FSRB in order to find the outliers automatically
load hprice.txt;
% setup parameters
n=size(hprice,1);
y=hprice(:,1);
X=hprice(:,2:5);
bayes=struct;
n0=5;
bayes.n0=n0;
% set \beta components
beta0=0*ones(5,1);
beta0(2,1)=10;
beta0(3,1)=5000;
beta0(4,1)=10000;
beta0(5,1)=10000;
bayes.beta0=beta0;
% \tau
s02=1/4.0e-8;
tau0=1/s02;
bayes.tau0=tau0;
% R prior settings
R=2.4*eye(5);
R(2,2)=6e-7;
R(3,3)=.15;
R(4,4)=.6;
R(5,5)=.6;
R=inv(R);
bayes.R=R;
% Automatic outlier detection procedure.
outBA=FSRB(y,X,'bayes',bayes', 'plots',0);
dout=n-length(outBA.ListOut);
% init = initial point to start monitoring
init=250;
xlimL=init; % lower value fo xlim
xlimU=n+1;  % upper value of xlim 
out=FSRBeda(y,X,'bayes',bayes,'init',init, 'conflev', [0.95 0.99]);
% Set font size, line width and line style
figure;
lwd=2.5;
FontSize=14;
linst={'-','--',':','-.','--',':'};
for j=1:5
my_subplot=subplot(3,2,j);
hold('on')
% plot 95% and 99% HPD  trajectories
plot(out.beta1(:,1),out.beta1HPD(:,1:2,j),'LineStyle',linst{4},'LineWidth',lwd,'Color','b')
plot(out.beta1(:,1),out.beta1HPD(:,3:4,j),'LineStyle',linst{4},'LineWidth',lwd,'Color','r')
% plot posterior estimate of beta1_j
plot(out.beta1(:,1),out.beta1(:,j+1)','LineStyle',linst{1},'LineWidth',lwd,'Color','k')
% Add the horizontal line which corresponds to prior values
xL = get(my_subplot,'XLim');
line(xL,[beta0(j) beta0(j)],'Color','r','LineWidth',lwd);
% Set ylim
ylimU=max([out.beta1HPD(:,4,j); beta0(j)]);
ylimL=min([out.beta1HPD(:,3,j); beta0(j)]);
ylim([ylimL ylimU])
% Set xlim
xlim([xlimL xlimU]);
% Add vertical line in correspondence of the step prior to the
% entry of the first outlier
line([dout; dout],[ylimL; ylimU],'Color','r','LineWidth',lwd);
ylabel(['$\hat{\beta_' num2str(j-1) '}$'],'Interpreter','LaTeX','FontSize',20,'rot',-360);
set(gca,'FontSize',FontSize);
if j>4
xlabel('Subset size m','FontSize',FontSize);
end
end
% Subplot associated with the monitoring of sigma^2
subplot(3,2,6);
%figure()
hold('on')
% 99%
plot(out.sigma21HPD(:,1),out.sigma21HPD(:,4:5),'LineStyle',linst{4},'LineWidth',lwd,'Color','r')
% 95%
plot(out.sigma21HPD(:,1),out.sigma21HPD(:,2:3),'LineStyle',linst{2},'LineWidth',lwd,'Color','b')
% Plot 1/tau1
plot(out.S21(:,1),1./out.S21(:,3),'LineWidth',lwd,'Color','k')
ylabel('$\hat{\sigma}^2$','Interpreter','LaTeX','FontSize',20,'rot',-360);
set(gca,'FontSize',FontSize);
% Set ylim
ylimU=max([out.sigma21HPD(:,5); s02]);
ylimL=min([out.sigma21HPD(:,4); s02]);
ylim([ylimL ylimU])
% Set xlim
xlim([xlimL xlimU]);
xL = get(my_subplot,'XLim');
% Add the horizontal line which corresponds to prior value of $\sigma^2$
line(xL,[s02 s02],'Color','r','LineWidth',lwd);
% Add vertical line in correspondence of the step prior to the
% entry of the first outlier
line([dout; dout],[ylimL; ylimU],'Color','r','LineWidth',lwd);
xlabel('Subset size m','FontSize',FontSize);
% Add multiple title
suplabel(['Housing data; forward plots in the interval ['...
num2str(xlimL) ',' num2str(xlimU) ...
']  of HPD regions for \beta and \sigma^2'],'t');
    Observed curve of r_min is at least 10 times greater than 99.99% envelope
--------------------------------------------------
-------------------------
Signal detection loop
Tentative signal in central part of the search: step m=511 because
rmin(511,546)>99.99% and rmin(510,546)>99.99% and rmin(512,546)>99.99%
rmin(511,546)>99.999%

-------------------
Signal validation exceedance of upper envelopes
Validated signal
-------------------------------
Start resuperimposing envelopes from step m=510
Superimposition stopped because r_{min}(512,529)>99.9% envelope
Subsample of 528 units is homogeneous
----------------------------
Final output
Number of units declared as outliers=18
Summary of the exceedances
           1          99         999        9999       99999
          10          64          48          38          29

m=100
m=200
m=300
m=400
m=500
    Click here for the graphical output of this example (link to Ro.S.A. website)

  • Plot of HPDI for BankProfit data.

    • XX=load('BankProfit.txt');
R=load('BankProfitR.txt');
X=XX(:,1:end-1);
y=XX(:,end);
% Load prior information
beta0=zeros(10,1);
beta0(1,1)=-0.5;        % 
beta0(2,1)=9.1;         % Number of products (NUMPRO)
beta0(3,1)=0.001;       % direct revenues  (DIRREV)
beta0(4,1)=0.0002;      % indirect revenues   (INDREV)
beta0(5,1)=0.002;       %  savings accounts   SAVACC
beta0(6,1)=0.12;        %  number of operations   NUMOPE
beta0(7,1)=0.0004;      %  total amount of operations  TOTOPE
beta0(8,1)=-0.0004;     %  Bancomat POS
beta0(9,1)=1.3;         %  Number of cards   NUMCAR
beta0(10,1)=0.00004;    %  Amount in cards   TOTCAR
% \tau
s02=10000;
tau0=1/s02;
% number of obs in which prior was based
n0=1500;
bayes=struct;
bayes.R=R;
bayes.n0=n0;
bayes.beta0=beta0;
bayes.tau0=tau0;
n=length(y);
% run routine FSRB in order to find the outliers automatically
outBA=FSRB(y,X,'bayes',bayes', 'plots',0);
dout=n-length(outBA.ListOut);
% init = point to start monitoring diagnostics along the FS
init=1700;
xlimL=init;
xlimU=n+1;
outBAeda=FSRBeda(y,X,'bayes',bayes,'init',init, 'conflev', [0.95 0.99]);
% Set font size, line width and line style
figure;
lwd=2.5;
FontSize=14;
linst={'-','--',':','-.','--',':'};
nr=4;
nc=3;
for j=1:length(beta0)
my_subplot=subplot(nr,nc,j);
hold('on')
% plot 95% and 99% HPD  trajectories
plot(outBAeda.beta1(:,1),outBAeda.beta1HPD(:,1:2,j),'LineStyle',linst{4},'LineWidth',lwd,'Color','b')
plot(outBAeda.beta1(:,1),outBAeda.beta1HPD(:,3:4,j),'LineStyle',linst{4},'LineWidth',lwd,'Color','r')
% plot posterior estimate of beta1_j
plot(outBAeda.beta1(:,1),outBAeda.beta1(:,j+1)','LineStyle',linst{1},'LineWidth',lwd,'Color','k')
% Add the horizontal line which corresponds to prior values
xL = get(my_subplot,'XLim');
line(xL,[beta0(j) beta0(j)],'Color','r','LineWidth',lwd);
% Set ylim
ylimU=max([outBAeda.beta1HPD(:,4,j); beta0(j)]);
ylimL=min([outBAeda.beta1HPD(:,3,j); beta0(j)]);
ylim([ylimL ylimU])
% Set xlim
xlim([xlimL xlimU]);
% Add vertical line in correspondence of the step prior to the
% entry of the first outlier
line([dout; dout],[ylimL; ylimU],'Color','r','LineWidth',lwd);
ylabel(['$\hat{\beta_' num2str(j-1) '}$'],'Interpreter','LaTeX','FontSize',20,'rot',-360);
set(gca,'FontSize',FontSize);
if j>nr*(nc-1)
xlabel('Subset size m','FontSize',FontSize);
end
end
% Subplot associated with the monitoring of sigma^2
subplot(4,3,11);
%figure()
hold('on')
% 99%
plot(outBAeda.sigma21HPD(:,1),outBAeda.sigma21HPD(:,4:5),'LineStyle',linst{4},'LineWidth',lwd,'Color','r')
% 95%
plot(outBAeda.sigma21HPD(:,1),outBAeda.sigma21HPD(:,2:3),'LineStyle',linst{2},'LineWidth',lwd,'Color','b')
% Plot 1\/tau1
plot(outBAeda.S21(:,1),1./outBAeda.S21(:,3),'LineWidth',lwd,'Color','k')
ylabel('$\hat{\sigma}^2$','Interpreter','LaTeX','FontSize',20,'rot',-360);
set(gca,'FontSize',FontSize);
% Set ylim
ylimU=max([outBAeda.sigma21HPD(:,5); s02]);
ylimL=min([outBAeda.sigma21HPD(:,4); s02]);
ylim([ylimL ylimU])
ylimL=8000;
ylimU=14000;
ylim([ylimL ylimU])
% Set xlim
xlim([xlimL xlimU]);
xL = get(my_subplot,'XLim');
% Add the horizontal line which corresponds to prior value of $\sigma^2$
line(xL,[s02 s02],'Color','r','LineWidth',lwd);
% Add vertical line in correspondence of the step prior to the
% entry of the first outlier
line([dout; dout],[ylimL; ylimU],'Color','r','LineWidth',lwd);
xlabel('Subset size m','FontSize',FontSize);
% Add multiple title
suplabel(['Bank profit data; forward plots in the interval ['...
num2str(xlimL) ',' num2str(xlimU) ...
']  of HPD regions for \beta and \sigma^2'],'t');

    Input Arguments

    expand all

    y — A vector with n elements that contains the response variables. Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.

    Data Types: single| double

    X — Data matrix of explanatory variables (also called 'regressors') of dimension (n x p-1). Rows of X represent observations, and columns represent variables.

    Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.

    PRIOR INFORMATION $\beta$ is assumed to have a normal distribution with mean $\beta_0$ and (conditional on $\tau_0$) covariance $(1/\tau_0) (X_0'X_0)^{-1}$.

    $\beta \sim N( \beta_0, (1/\tau_0) (X_0'X_0)^{-1} )$

    Data Types: single| double

    Name-Value Pair Arguments

    Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

    Example: 'intercept',false , bayes=struct;bayes.R=R;bayes.n0=n0;bayes.beta0=beta0;bayes.tau0=tau0; , bsb=[2 5 1]; , 'init',100 starts monitoring from step m=100 , 'nocheck',true , 'conflev',[0.90 0.93]

    intercept —Indicator for constant term.true (default) | false.

    Indicator for the constant term (intercept) in the fit, specified as the comma-separated pair consisting of 'Intercept' and either true to include or false to remove the constant term from the model.

    Example: 'intercept',false

    Data Types: boolean

    bayes —It specifies prior information.structure.

    A structure which specifies prior information.

    If structure bayes is not supplied the default values which are used are: beta0= zeros(p,1) (vector of zeros); R=eye(p) (Identity matrix); tau0=1/1e+6 (very large value for the prior variance, that is a very small value for tau0); n0=1 (just one prior observation).

    Strucure bayes contains the following fields:

    Value Description
    beta0

    p-times-1 vector containing prior mean of $\beta$
    R

    p-times-p positive definite matrix which can be interepreted as $X_0'X_0$ where $X_0$ is a n0 x p matrix coming from previous experiments (assuming that the intercept is included in the model)
    tau0

    scalar. Prior estimate of $\tau=1/ \sigma^2=a_0/b_0$.

    The prior distribution of tau0 is a gamma distribution with parameters a and b, that is $p(\tau_0) \propto \tau^{a_0-1} \exp (-b_0 \tau)$;

    $E(\tau_0)= a_0/b_0$.
    n0

    scalar. Sometimes it helps to think of the prior information as coming from n0 previous experiments.

    Therefore we assume that matrix $X_0$ (which defines R), was made up of n0 observations.

    Example: bayes=struct;bayes.R=R;bayes.n0=n0;bayes.beta0=beta0;bayes.tau0=tau0;

    Data Types: double

    bsb —list of units forming the initial subset.vector.

    if bsb=0 then the procedure starts with p units randomly chosen else if bsb is not 0 the search will start with m0=length(bsb). The default value of bsb is '' that is in the first step just prior information is used.

    Example: bsb=[2 5 1];

    Data Types: double

    init —Search initialization.scalar.

    scalar, specifies the point where to start monitoring required diagnostics. if init is not specified it will be set equal to : p+1, if the sample size is smaller than 40;

    min(3*p+1,floor(0.5*(n+p+1))), otherwise.

    Example: 'init',100 starts monitoring from step m=100

    Data Types: double

    nocheck —Check input arguments.boolean.

    Scalar. If nocheck is equal to true no check is performed on matrix y and matrix X. Notice that y and X are left unchanged. In other words the additional column of ones for the intercept is not added. As default nocheck=false. See routine chkinputRB for the details of the operations.

    Example: 'nocheck',true

    Data Types: boolean

    conflev —confidence levels to be used to compute HPDI.vector.

    This input option is used just if input stats=1. The default value of conflev is [0.95 0.99] that is 95% and 99% HPDI confidence intervals are computed.

    Example: 'conflev',[0.90 0.93]

    Data Types: double

    Output Arguments

    expand all

    out — description Structure

    T consists of a structure 'out' containing the following fields:

    Value Description
    RES

    Scaled residuals. Matrix.

    n x (n-init+1) matrix containing the monitoring of scaled residuals.

    1st row = residual for first unit;

    ...;

    nth row = residual for nth unit.
    LEV

    Leverage. Matrix.

    (n+1) x (n-init+1) = matrix containing the monitoring of leverage.

    1st row = leverage for first unit;

    ...;

    nth row = leverage for nth unit.
    BB

    n x (n-init+1) matrix containing the information about the units belonging to the subset at each step of the forward search.

    1st col = indexes of the units forming subset in the initial step;

    ...;

    last column = units forming subset in the final step (all units).
    mdrB

    n-init x 3 matrix which contains the monitoring of Bayesian minimum deletion residual or (m+1)ordered residual at each step of the forward search.

    1st col = fwd search index (from init to n-1);

    2nd col = minimum deletion residual;

    3rd col = (m+1)-ordered residual.

    Remark: these quantities are stored with sign, that is the min deletion residual is stored with negative sign if it corresponds to a negative residual.
    msrB

    n-init+1 x 32= matrix which contains the monitoring of maximum studentized residual among units belonging to subset.

    1st col = fwd search index (from init to n);

    2nd col = maximum studentized residual.
    Coo

    (n-init+1) x 2 matrix containing the monitoring of Cook or modified Cook distance in each step of the forward search.

    1st col = fwd search index (from init to n);

    2nd col = monitoring of Cook distance.
    beta1

    (n-init+1) x (p+1) matrix containing the monitoring of posterior mean of $\beta$ (regression coefficents) $\beta_1 = (c*R + X'X)^{-1} (c*R*\beta_0 + X'y)$
    Gam

    (n-init+1) x 3 matrix containing: 1st col = fwd search index (from init to n);

    2nd col = shape parameter $a_1$ of the posterior gamma distribution of tau;

    3rd col = scale parameter $b_1$ of the posterior gamma distribution of tau.

    Remark: $a_1 = 0.5 (c*n0 + m)$ where m is subset size;

    $b_1 = 0.5 * ( n0 / \tau_0 + (y-X*\beta_1)'y +(\beta_0-\beta_1)'*c*R*\beta_0 )$
    covbeta1

    p x p x (n-init+1) 3D array containing posterior covariance matrix (conditional on $tau_1$) of $\beta$.

    $cov(\beta_1) = (1/tau_1) * (c*R + X'X)^{-1}$;

    where $tau_1$ is defined as $a_1/b_1$ (that is through the gamma parameters of the posterior distribution of $\tau$).

    The posterior distribution of $\tau$ is a gamma distribution with parameters $a_1$ and $b_1$.
    S21

    (n-init+1) x 3 matrix containing the monitoring of posterior estimate of $\sigma^2$ and $\tau$ in each step of the forward search.

    1st col = fwd search index (from init to n);

    2nd col = monitoring of $\sigma^2_1$ (posterior estimate of $\sigma^2$);

    3rd col = monitoring $\tau_1$ (posterior estimate of $\tau$).
    Bpval

    (n-init+1) x (p+1) containing Bayesian p-values.

    p-value = $P(|t| > | \hat{\beta} / se(beta) |)$ = prob. of beta different from 0.

    1st col = fwd search index (from init to n);

    2nd col = p-value for first variable;

    ...;

    (p+1) col = p-value for p-th variable.
    beta1HPD

    (n-init+1)-by-2-by-p 3D array.

    Bhpd(:,:,1) = lower and upper HPDI of first element of $\beta_1$ (posterior estimate of $\beta$);

    ...;

    Bhpd(:,:,p) = lower and upper HPDI of last element of $\beta_1$ (posterior estimate of $\beta$).
    tau1HPD

    (n-init+1) x 3 containing HPDI for $\tau_1$.

    1st col = fwd search index (from init to n);

    2nd col = lower value of HPDI;

    3rd col = upper value of HPDI;
    sigma21HPD

    (n-init+1) x 3 containing HPDI for $\sigma^2_1$.

    1st col = fwd search index (from init to n);

    2nd col = lower value of HPDI;

    3rd col = upper value of HPDI.
    postodds

    (n-init+1)-by-(p+1) matrix which contains posterior odds for $\beta_j=0$.

    For example the posterior odd of $\beta_0=0$ is p(y| model which contains all expl variables except the one associated with beta0) divided by p(y| model which contains all expl variables).

    1st col = fwd search index (from init to n);

    2nd col = posterior odd for $beta_1$;

    ...;

    (p+1) col = posterior odd for $beta_p$.
    modelprob

    (n-init+1)-by-(p+1) matrix which contains posterior model probability of the model which excludes variable j. For example if modelprob(j)= 0.28, that is if the probability of the model which does not contain variable j is equal to 0.28, it means that there is a 28 chance that beta_j=0 and a 72 chance that it is not.

    1st col = fwd search index (from init to n);

    2nd col = posterior model prob of the model which excludes $\beta_1$;

    ...;

    (p+1) col = posterior model prob of the model which excludes $beta_p$.
    Un

    (n-init) x 11 matrix which contains the unit(s) included in the subset at each step of the fwd search.

    REMARK: in every step the new subset is compared with the old subset. Un contains the unit(s) present in the new subset but not in the old one Un(1,2) for example contains the unit included in step init+1 Un(end,2) contains the units included in the final step of the search.
    y

    A vector with n elements that contains the response variable which has been used.
    X

    Data matrix of explanatory variables which has been used (it also contains the column of ones if input option intercept was missing or equal to true).
    class

    'FSRBeda'.

    References

    Chaloner, K. and Brant, R. (1988), A Bayesian Approach to Outlier Detection and Residual Analysis, "Biometrika", Vol. 75, pp. 651-659.

    Riani, M., Corbellini, A. and Atkinson, A.C. (2018), Very Robust Bayesian Regression for Fraud Detection, "International Statistical Review", http://dx.doi.org/10.1111/insr.12247

    Atkinson, A.C., Corbellini, A. and Riani, M., (2017), Robust Bayesian Regression with the Forward Search: Theory and Data Analysis, "Test", Vol. 26, pp. 869-886, https://doi.org/10.1007/s11749-017-0542-6

    See Also

    | |

    This page has been automatically generated by our routine publishFS