FSRtsmdr

FSRtsmdr computes minimum deletion residual for time series models in each step of the search

expand all in page

Syntax

  • mdr=FSRtsmdr(y,bsb)example
  • mdr=FSRtsmdr(y,bsb,Name,Value)example
  • [mdr,Un]=FSRtsmdr(___)example
  • [mdr,Un,BB]=FSRtsmdr(___)example
  • [mdr,Un,BB,Bols]=FSRtsmdr(___)example
  • [mdr,Un,BB,Bols,S2]=FSRtsmdr(___)example
  • [mdr,Un,BB,Bols,S2,Exflag]=FSRtsmdr(___)example

Description

example

mdr =FSRtsmdr(y, bsb) FSRtsmdr with all default options.

example

mdr =FSRtsmdr(y, bsb, Name, Value) FSRtsmdr with optional arguments.

example

[mdr, Un] =FSRtsmdr(___) Analyze units entering the search in the final steps.

example

[mdr, Un, BB] =FSRtsmdr(___) Store units forming subsets in selected steps.

example

[mdr, Un, BB, Bols] =FSRtsmdr(___) Example where initial subset comes from LTSts.

example

[mdr, Un, BB, Bols, S2] =FSRtsmdr(___)

example

[mdr, Un, BB, Bols, S2, Exflag] =FSRtsmdr(___)

Examples

expand all

  • FSRtsmdr with all default options.

    • linear trend + just one harmonic for seasonal Common part to all examples: load airline dataset. 

    %   1949 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959 1960
y = [112  115  145  171  196  204  242  284  315  340  360  417    % Jan
118  126  150  180  196  188  233  277  301  318  342  391    % Feb
132  141  178  193  236  235  267  317  356  362  406  419    % Mar
129  135  163  181  235  227  269  313  348  348  396  461    % Apr
121  125  172  183  229  234  270  318  355  363  420  472    % May
135  149  178  218  243  264  315  374  422  435  472  535    % Jun
148  170  199  230  264  302  364  413  465  491  548  622    % Jul
148  170  199  242  272  293  347  405  467  505  559  606    % Aug
136  158  184  209  237  259  312  355  404  404  463  508    % Sep
119  133  162  191  211  229  274  306  347  359  407  461    % Oct
104  114  146  172  180  203  237  271  305  310  362  390    % Nov
118  140  166  194  201  229  278  306  336  337  405  432 ]; % Dec
y=(y(:));
% Monitor minimum deletion residual in each step of the forward search.
% Start from a random subset. The final part of the trajectory is
% completely unaffected by the starting point.
% Plot the trajectory of mdr.
mdr=FSRtsmdr(y,0,'plots',1);

  • FSRtsmdr with optional arguments.

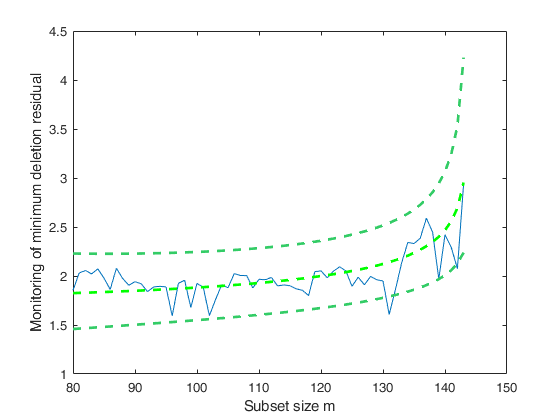
    • Compute minimum deletion residual and start monitoring it from step m=80. 

    %   1949 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959 1960
y = [112  115  145  171  196  204  242  284  315  340  360  417    % Jan
118  126  150  180  196  188  233  277  301  318  342  391    % Feb
132  141  178  193  236  235  267  317  356  362  406  419    % Mar
129  135  163  181  235  227  269  313  348  348  396  461    % Apr
121  125  172  183  229  234  270  318  355  363  420  472    % May
135  149  178  218  243  264  315  374  422  435  472  535    % Jun
148  170  199  230  264  302  364  413  465  491  548  622    % Jul
148  170  199  242  272  293  347  405  467  505  559  606    % Aug
136  158  184  209  237  259  312  355  404  404  463  508    % Sep
119  133  162  191  211  229  274  306  347  359  407  461    % Oct
104  114  146  172  180  203  237  271  305  310  362  390    % Nov
118  140  166  194  201  229  278  306  336  337  405  432 ]; % Dec
y=(y(:));
% Set up a personalized model.
model=struct;
model.trend=1;              % linear trend
model.s=12;                 % monthly time series
model.seasonal=104;         % four harmonics with time varying seasonality
% Choose step to start monitoring.
init=80;
out1=FSRtsmdr(y,0,'model',model,'init',80,'plots',1);

  • Analyze units entering the search in the final steps.

    • Common part to all examples: load airline dataset. 

    %   1949 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959 1960
y = [112  115  145  171  196  204  242  284  315  340  360  417    % Jan
118  126  150  180  196  188  233  277  301  318  342  391    % Feb
132  141  178  193  236  235  267  317  356  362  406  419    % Mar
129  135  163  181  235  227  269  313  348  348  396  461    % Apr
121  125  172  183  229  234  270  318  355  363  420  472    % May
135  149  178  218  243  264  315  374  422  435  472  535    % Jun
148  170  199  230  264  302  364  413  465  491  548  622    % Jul
148  170  199  242  272  293  347  405  467  505  559  606    % Aug
136  158  184  209  237  259  312  355  404  404  463  508    % Sep
119  133  162  191  211  229  274  306  347  359  407  461    % Oct
104  114  146  172  180  203  237  271  305  310  362  390    % Nov
118  140  166  194  201  229  278  306  336  337  405  432 ]; % Dec
y=(y(:));
% Compute minimum deletion residual and analyze the units entering
% subset in each step of the fwd search (matrix Un).  As is well known,
% the FS provides an ordering of the data from those most in agreement
% with a suggested model (which enter the first steps) to those least in
% agreement with it (which are included in the final steps).
% Set up a personalized model.
model=struct;
model.trend=1;              % linear trend
model.s=12;                 % monthly time series
model.seasonal=104;         % four harmonics with time varying seasonality
% Choose step to start monitoring.
init=80;
[mdr,Un,BB,Bols,S2,Exflag]=FSRtsmdr(y,0,'model',model,'init',80,'plots',1);
% Check if there was convergence in all step which were monitored.
if min(Exflag(:,2))<1
disp('Warning: in some steps there was not convergence')
else
disp('Convergence obtained in all steps')
end
% Check the last two units which are included in the last two steps.
disp(Un(end-1:end,:))
    Convergence obtained in all steps
   143   139   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN
   144   142   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN
    Click here for the graphical output of this example (link to Ro.S.A. website).

  • Store units forming subsets in selected steps.

    • In this example the units forming subset are stored just for selected steps. 

    %   1949 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959 1960
y = [112  115  145  171  196  204  242  284  315  340  360  417    % Jan
118  126  150  180  196  188  233  277  301  318  342  391    % Feb
132  141  178  193  236  235  267  317  356  362  406  419    % Mar
129  135  163  181  235  227  269  313  348  348  396  461    % Apr
121  125  172  183  229  234  270  318  355  363  420  472    % May
135  149  178  218  243  264  315  374  422  435  472  535    % Jun
148  170  199  230  264  302  364  413  465  491  548  622    % Jul
148  170  199  242  272  293  347  405  467  505  559  606    % Aug
136  158  184  209  237  259  312  355  404  404  463  508    % Sep
119  133  162  191  211  229  274  306  347  359  407  461    % Oct
104  114  146  172  180  203  237  271  305  310  362  390    % Nov
118  140  166  194  201  229  278  306  336  337  405  432 ]; % Dec
y=(y(:));
model=struct;
model.trend=1;              % linear trend
model.s=12;                 % monthly time series
model.seasonal=104;         % four harmonics with time varying seasonality
init=80;
[mdr,Un,BB,Bols,S2] =FSRtsmdr(y,0,'model',model,'init',80,'bsbsteps',[90 120]);
% BB has just two columns
% First column contains information about units forming subset at step m=90
% sum(~isnan(BB(:,1))) is 90
% Second column contains information about units forming subset at step m=120
% sum(~isnan(BB(:,2))) is 120
disp(sum(~isnan(BB(:,1))))
disp(sum(~isnan(BB(:,2))))
        90

   120

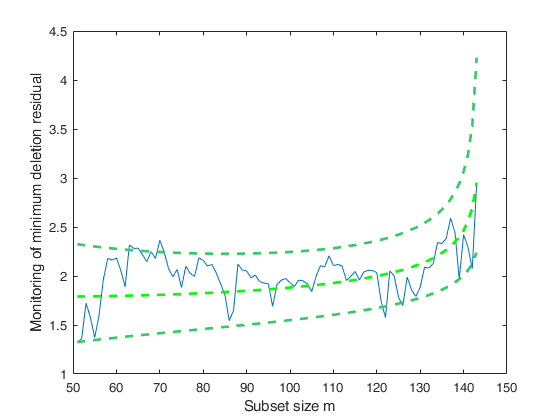
  • Example where initial subset comes from LTSts.

    • In this example the units forming subset are stored just for selected steps. 

    %   1949 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959 1960
y = [112  115  145  171  196  204  242  284  315  340  360  417    % Jan
118  126  150  180  196  188  233  277  301  318  342  391    % Feb
132  141  178  193  236  235  267  317  356  362  406  419    % Mar
129  135  163  181  235  227  269  313  348  348  396  461    % Apr
121  125  172  183  229  234  270  318  355  363  420  472    % May
135  149  178  218  243  264  315  374  422  435  472  535    % Jun
148  170  199  230  264  302  364  413  465  491  548  622    % Jul
148  170  199  242  272  293  347  405  467  505  559  606    % Aug
136  158  184  209  237  259  312  355  404  404  463  508    % Sep
119  133  162  191  211  229  274  306  347  359  407  461    % Oct
104  114  146  172  180  203  237  271  305  310  362  390    % Nov
118  140  166  194  201  229  278  306  336  337  405  432 ]; % Dec
y=(y(:));
% Set up the model.
model=struct;
model.trend=1;              % linear trend
model.s=12;                 % monthly time series
model.seasonal=104;         % four harmonics with time varying seasonality
% Call LTSts
out=LTSts(y,'model',model');
% Extract best initial subset from LTSts.
[~,indres]=sort(abs(out.residuals));
bs=indres(1:50);
[mdr,Un,BB,Bols,S2,Exflag] =FSRtsmdr(y,bs,'model',model,'init',length(bs)+1,'plots',1);
    Click here for the graphical output of this example (link to Ro.S.A. website).

    Input Arguments

    expand all

    y — Time series to analyze. Vector.

    A row or a column vector with T elements, which contains the time series.

    Data Types: single| double

    bsb — list of units forming the initial subset. Vector.

    If bsb=0 (default) then the procedure starts with p units randomly chosen else if bsb is not 0 the search will start with m0=length(bsb). p is the total number of regression parameters which have to be estimated.

    Data Types: single| double

    Name-Value Pair Arguments

    Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

    Example: 'init',100 starts monitoring from step m=100 , 'model', model , 'plots',1 , 'nocheck',true , 'msg',1 , 'bsbmfullrank',1 ,

    init —Start of monitoring point.scalar.

    It specifies the point where to initialize the search and start monitoring required diagnostics. If it is not specified it is set equal floor(0.5*(T+1))

    Example: 'init',100 starts monitoring from step m=100

    Data Types: double

    model —model type.structure.

    A structure which specifies the model which will be used. The model structure contains the following fields:

    Value Description
    s

    scalar (length of seasonal period). For monthly data s=12 (default), for quartely data s=4, ...
    trend

    scalar (order of the trend component).

    trend = 1 implies linear trend with intercept (default), trend = 2 implies quadratic trend ...

    Admissible values for trend are, 0, 1, 2 and 3.
    seasonal

    scalar (integer specifying number of frequencies, i.e. harmonics, in the seasonal component. Possible values for seasonal are $1, 2, ..., [s/2]$, where $[s/2]=floor(s/2)$.

    For example: if seasonal =1 (default) we have: $\beta_1 \cos( 2 \pi t/s) + \beta_2 sin ( 2 \pi t/s)$;

    if seasonal =2 we have: $\beta_1 \cos( 2 \pi t/s) + \beta_2 \sin ( 2 \pi t/s) + \beta_3 \cos(4 \pi t/s) + \beta_4 \sin (4 \pi t/s)$.

    Note that when $s$ is even the sine term disappears for $j=s/2$ and so the maximum number of trigonometric parameters is $s-1$.

    If seasonal is a number greater than 100 then it is possible to specify how the seasonal component grows over time.

    For example, seasonal =101 implies a seasonal component which just uses one frequency which grows linearly over time as follows: $(1+\beta_3 t)\times ( \beta_1 cos( 2 \pi t/s) + \beta_2 \sin ( 2 \pi t/s))$.

    For example, seasonal =201 implies a seasonal component which just uses one frequency which grows in a quadratic way over time as follows: $(1+\beta_3 t + \beta_4 t^2)\times( \beta_1 \cos( 2 \pi t/s) + \beta_2 \sin ( 2 \pi t/s))$.

    seasonal =0 implies a non seasonal model.
    X

    matrix of size T-by-nexpl containing the values of nexpl extra covariates which are likely to affect y.
    posLS

    positive integer which specifies to position to include the level shift component.

    For example if model.posLS =13 then the explanatory variable $I(t \geq 13})$ is created.

    If this field is not present or if it is empty, the level shift component is not included.
    B

    column vector or matrix containing the initial values of parameter estimates which have to be used in the maximization procedure. If model.B is a matrix, then initial estimates are extracted from the first colum of this matrix. If this field is empty or if this field is not present, the initial values to be used in the maximization procedure are referred to the OLS parameter estimates of the linear part of the model. The parameters associated to time varying amplitude are initially set to 0.

    Remark: the default model is for monthly data with a linear trend (2 parameters) + seasonal component with just one harmonic (2 parameters), no additional explanatory variables and no level shift that is model=struct;

    model.s=12;

    model.trend=1;

    model.seasonal=1;

    model.X='';

    model.posLS='';

    Example: 'model', model

    Data Types: struct

    plots —Plot on the screen.scalar.

    If equal to one a plot of minimum deletion residual appears on the screen with 1%, 50% and 99% confidence bands else (default) no plot is shown.

    Remark: the plot which is produced is very simple. In order to control a series of options in this plot and in order to connect it dynamically to the other forward plots it is necessary to use function mdrplot.

    Example: 'plots',1

    Data Types: double

    nocheck —Check input arguments inside structure model.as default nocheck=false.

    Example: 'nocheck',true

    Data Types: boolean

    msg —Level of output to display.scalar.

    It controls whether to display or not messages about great interchange on the screen If msg==1 (default) messages are displayed on the screen else no message is displayed on the screen

    Example: 'msg',1

    Data Types: double

    constr —Constrained search.vector.

    r x 1 vector which contains the list of units which are forced to join the search in the last r steps. The default is constr=''. No constraint is imposed

    Example: 'constr',[1:10] forces the first 10 units to join the subset in the last 10 steps

    Data Types: double

    bsbmfullrank —What to do in case subset at step m (say bsbm) produces a non singular X.scalar.

    This options controls what to do when rank(X(bsbm,:)) is smaller then number of explanatory variables.

    If bsbmfullrank = 1 (default is 1) these units (whose number is say mnofullrank) are constrained to enter the search in the final n-mnofullrank steps else the search continues using as estimate of beta at step m the estimate of beta found in the previous step.

    Example: 'bsbmfullrank',1

    Data Types: double

    bsbsteps —Save the units forming subsets.vector.

    It specifies for which steps of the fwd search it is necessary to save the units forming subsets. If bsbsteps is 0 we store the units forming subset in all steps. The default is store the units forming subset in all steps if T<=5000, else to store the units forming subset at steps init and steps which are multiple of 100. For example, as default, if T=753 and init=6, units forming subset are stored for m=init, 100, 200, 300, 400, 500 and 600.

    Example: 'bsbsteps',[100 200] stores the unis forming subset in steps 100 and 200.

    Data Types: double

    Output Arguments

    expand all

    mdr —Monitoring of minimum deletion residual at each step of the forward search. T -init -by- 2 matrix

    1st col = fwd search index (from init to T-1).

    2nd col = minimum deletion residual.

    REMARK: if in a certain step of the search matrix is singular, this procedure checks how many observations produce a singular matrix. In this case mdr is a column vector which contains the list of units for which matrix X is non singular.

    Un —Units included in each step. Matrix

    (T-init) x 11 Matrix which contains the unit(s) included in the subset at each step of the search.

    REMARK: in every step the new subset is compared with the old subset. Un contains the unit(s) present in the new subset but not in the old one.

    Un(1,2) for example contains the unit included in step init+1.

    Un(end,2) contains the units included in the final step of the search.

    BB —Units belonging to subset in each step. Matrix

    T x (T-init+1) or T-by-length(bsbsteps) matrix (depending on input option bsbsteps) which contains information about the units belonging to the subset at each step of the forward search. BB has the following structure: 1-st row has number 1 in correspondence of the steps in which unit 1 is included inside subset and a missing value for the other steps;

    ......

    (T-1)-th row has number T-1 in correspondence of the steps in which unit T-1 is included inside subset and a missing value for the other steps;

    T-th row has number Tn in correspondence of the steps in which unit T is included inside subset and a missing value for the other steps The size of matrix BB is T x (T-init+1) if option input bsbsteps is 0 else the size is T-by-length(bsbsteps).

    Bols —beta coefficents. Matrix

    (T-init+1) x (p+1) matrix containing the monitoring of estimated beta coefficients in each step of the forward search.

    S2 —S2 and R2. Matrix

    (T-init+1) x 3 matrix containing the monitoring of S2 (2nd column)and R2 (third column) in each step of the forward search.

    Exflag —Reason nlinfit stopped. Integer matrix

    (T-init+1) x 2 matrix containing information about the result of the maximization procedure.

    If the model is non linear out.Exflag(i,2) is equal to 1 if at step out.Exflag(i,1) the maximization procedure did not produce warnings or the warning was different from "ILL Conditiioned Jacobian". For any other warning which is produced (for example, "Overparameterized", "IterationLimitExceeded", 'MATLAB:rankDeficientMatrix") out.Exflag(i,2) is equal to -1;

    References

    Atkinson, A.C. and Riani, M. (2006), Distribution theory and simulations for tests of outliers in regression, "Journal of Computational and Graphical Statistics", Vol. 15, pp. 460-476.

    Riani, M. and Atkinson, A.C. (2007), Fast calibrations of the forward search for testing multiple outliers in regression, "Advances in Data Analysis and Classification", Vol. 1, pp. 123-141.

    Rousseeuw, P.J., Perrotta D., Riani M. and Hubert, M. (2018), Robust Monitoring of Many Time Series with Application to Fraud Detection, "Econometrics and Statistics". [RPRH]

    See Also

    | |

    This page has been automatically generated by our routine publishFS