GUIpowermean
GUIpowermean shows the necessary calculations to obtain the power (generalized) mean in a GUI.
Description
The power mean (also known as generalized mean, or Holder mean or Kolmogorov-Negumo function of the mean), is an abstraction of the Pythagorean means. It includes the harmonic , geometric (s\rightarrow 0), and arithmetic (s=1), quadratic (s=2), cubic mean (s=3). When s \rightarrow -\infty the power mean tends to x_{min} and when s\rightarrow +\infty the power mean tends to x_{max}. http://en.wikipedia.org/wiki/Generalized_mean
Examples
Input Arguments
Output Arguments
References
Milioli, M.A., Riani, M., Zani, S. (2019), "Introduzione all'analisi dei dati statistici (Quarta edizione ampliata)". [MRZ]
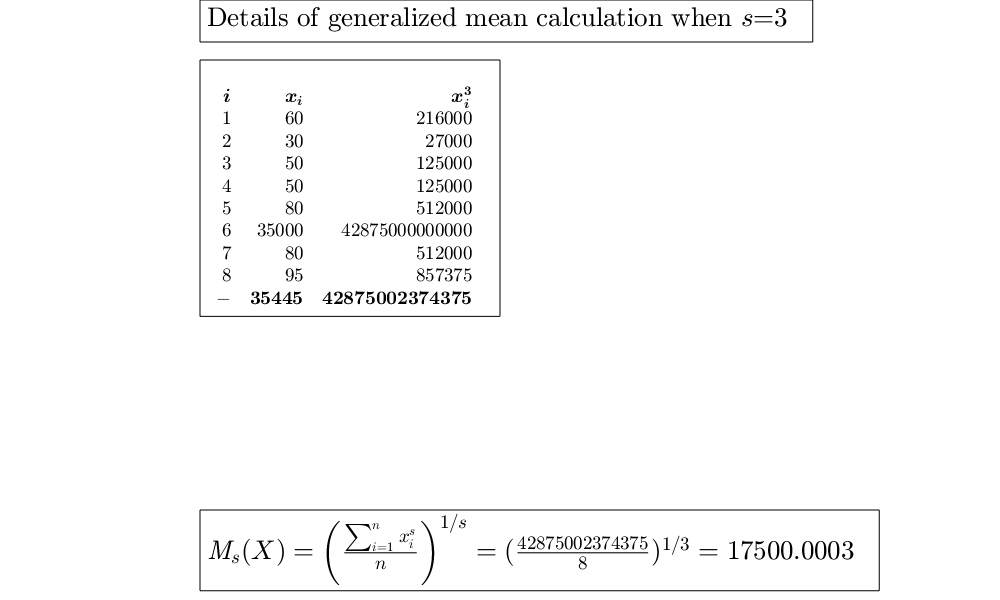
 Example of use of the cubic mean.
Example of use of the cubic mean.